均值/方差/标注查介绍
前言
在学习量化时,发现很多捕捉alpha信号的公式中都会涉及到均值、标准差、方差的使用。而在自己设计信号模板时,对于什么时候该使用哪一个统计特征并没有想法。因此在请教了大D老师后,讲学习记录及思考记录如下,便于自己之后需要时学习,也希望能为看到这篇文章的同志提供些帮助与启发。
均值
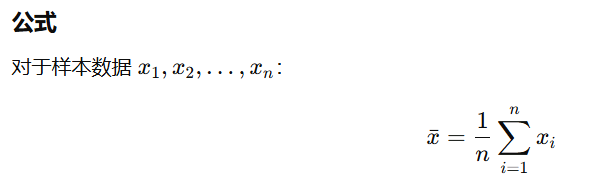
一组数据的“重心”,衡量数据的中心趋势
对异常值敏感,容易被单个极值拉偏
方差
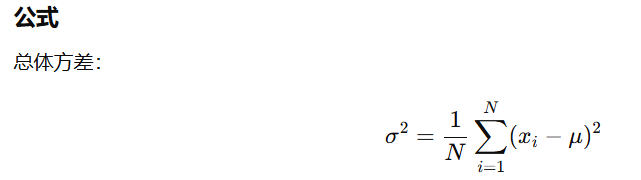
衡量数据与均值的偏离程度,反映数据的离散性:方差越大,数据整体距离均值越远;方差越小,数据整体距离均值越近
方差单位是原始数据单位的平方,不便于直观解释,所以很少用方差来阐述事物
标准差

方差的平方根,同样用来衡量数据与均值的偏离程度。标准差越大,数据整体距离均值越远;标注差越小,数据越集中在均值附近
和原始数据同单位,在同一量纲内,解释性更好。因此,在分析数据特征时,标准差使用频率应该高于方差
总结
均值用来表示数据分布的中心
标准差和方差用来表示数据围绕中心分布的宽度,或者称表示数据离散的程度。通过数据的离散程度可快速判断这一组数据的稳定性,是否有明显波动
可用来描述正态分布,可用来计算z-score分数,z-score使得不同量纲、不同尺度的数据可以比较
数据离散
之所以会有这个章节是因为在写这篇文章时,对于标准差和方差,我起初写的是“方差/标准差越大,数据越分散”,后来改成了“整体数据距离均值越远”。因为脑海里却浮现出 [10,10,10,10,10,0,0,0,0,0] 这样一组数据,直观上感觉,把这样一组称作分散是有待商榷的,毕竟是集中分布在两个区域。但在数学来讲,这组数据就是离散的,而且是典型的双峰分布。
统计学中的离散指数据只能取有限个值,不是连续的。数学中的离散指数据分布的集中程度。
