当前位置：首页 > news >正文

[网络入侵AI检测] 深度前馈神经网络（DNN）模型

news 2025/9/9 9:07:02

第4章：深度前馈神经网络（DNN）模型

欢迎回来🐻‍❄️

在第1章：分类任务配置（二分类 vs. 多分类）中，我们学习了如何配置模型以回答不同类型的问题；在第2章：数据加载与预处理中，我们成为了“数据大厨”，准备好了数据“食材”；最近，在第3章：经典机器学习模型中，我们探索了一套可靠的“手工工具”来检测入侵行为。

虽然经典模型非常强大，但有时网络攻击极其隐蔽且复杂。它们可能涉及一些细微的模式，简单的模型难以捕捉。想象一下，我们有一支安全警卫团队。有些警卫擅长检查基本的ID（经典模型），但对于真正复杂的威胁，我们需要一个高度专业化、多阶段的安全系统，其中包含层层互联的专家，每位专家在传递信息前都会对其进行精炼。

这就是深度前馈神经网络（DNN）模型的用武之地

这是我们迈向“深度学习”世界的第一步，深度学习是受人类大脑启发的模型。DNN能够揭示网络流量数据中极其复杂、非直观的关系，使其能够检测到最难以捉摸的入侵行为。

DNN解决了什么问题？

DNN旨在学习输入特征（如连接持续时间、协议、字节计数）与输出标签（如“正常”或“攻击”）之间的复杂非线性关系。经典模型可能难以处理那些无法通过简单直线或曲线轻松分隔的模式。而DNN通过其多层结构，本质上可以在数据中绘制高度复杂的波浪形边界，从而更精确地区分不同类型的网络流量。

我们的核心用例仍然是网络入侵检测，但现在我们装备了一个能够处理更深层次、更抽象攻击特征的模型。

DNN的关键概念

深度前馈神经网络通常也称为多层感知机（MLP）。它之所以“深”，是因为它在输入和输出之间有多个隐藏层。“前馈”意味着信息单向流动，从输入到输出，不会循环回来。

让我们分解其核心部分：

1. 神经元（节点）

将神经元想象为一个微小的决策单元。它接收输入，进行简单计算，然后将输出传递给下一个神经元。每个输入都有一个与之关联的权重（表示该输入的重要性），神经元还有一个偏置（添加到计算中的额外值）。模型通过调整这些权重和偏置来学习。

2. 层：决策的各个阶段

神经元被组织成层，形成我们安全系统的“阶段”：

输入层：这是原始处理数据（来自第2章：数据加载与预处理的网络连接的41个特征）进入网络的地方。每个特征都有自己的“输入神经元”。
隐藏层（密集层）：这是DNN的核心。它们被称为“隐藏”是因为它们不直接与外界（输入或输出）交互。在这些层中，神经元是“密集连接”的——即一层中的每个神经元都与下一层中的每个神经元相连。这使得它们能够处理和转换来自前一层的信息，学习越来越复杂的特征。DNN至少有一个隐藏层，通常有很多。
输出层：这是给出模型预测的最终层。正如我们在第1章：分类任务配置（二分类 vs. 多分类）中学到的，其配置取决于我们是进行二分类（1个神经元，sigmoid激活）还是多分类（N个神经元，softmax激活）。

3. 激活函数：添加非线性

在神经元计算其输入的加权和加上偏置后，“激活函数”决定是否以及如何“激活”（产生输出）。

relu（修正线性单元）：这是隐藏层中非常常见的激活函数。它很简单：如果输入为正，则直接输出；如果为负，则输出零。这种非线性对于DNN学习复杂模式至关重要，而不仅仅是简单的直线。
sigmoid / softmax：如第1章所述，这些是专门用于分类任务的输出层的激活函数。

4. Dropout层：防止过拟合

想象一下，我们的安全警卫变得过于擅长记住训练中的特定面孔，但在面对稍有不同新面孔时却无法识别。这就是过拟合——模型对训练数据记忆得太好，失去了对新数据的泛化能力。

Dropout层是一个聪明的技巧，可以防止这种情况。在训练过程中，Dropout层会随机“关闭”一层中一定比例的神经元。这迫使剩余的神经元学习更鲁棒的特征，并防止任何单个神经元过度依赖其他神经元。这就像强制不同的安全警卫轮流休息，确保整个团队都具备能力，而不是只有一个明星。

如何构建用于入侵检测的DNN

我们将使用Keras（一个用户友好的神经网络构建库）来构建我们的DNN。基本步骤如下：

启动一个Sequential模型：这是一个简单的层堆叠。
添加Dense层：这些是我们的隐藏层，使用relu激活。
添加Dropout层：防止过拟合。
添加Dense输出层：根据第1章配置为二分类或多分类。
编译模型：告诉它如何学习（优化器）以及测量什么（损失函数、指标）。
训练模型：输入准备好的数据。

让我们看一个简化示例。假设X_train包含我们归一化的网络特征，y_train包含标签，如第2章和第1章所述。

示例代码：用于二分类的简单DNN

以下是如何构建一个带有一个隐藏层的基本DNN用于二分类入侵检测：

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
import numpy as np # 用于数据创建示例# --- 假设 X_train 和 y_train 已从第2章准备好 ---
# 为了演示，我们创建一些虚拟数据：
# 1000个样本，每个样本41个特征
X_train_dummy = np.random.rand(1000, 41)
# 1000个二分类标签（0或1）
y_train_dummy = np.random.randint(0, 2, 1000)# 1. 开始定义网络（层的堆叠）
model = Sequential()# 2. 添加第一个（也是唯一的）隐藏层：一个Dense层
#    - 1024个神经元（可以自行选择数量）
#    - input_dim=41：告诉模型输入有41个特征
#    - activation='relu'：隐藏层的激活函数
model.add(Dense(1024, input_dim=41, activation='relu'))# 3. 添加一个Dropout层
#    - 0.01表示训练期间随机“关闭”1%的神经元
model.add(Dropout(0.01))# 4. 添加输出层（用于二分类，如第1章所述）
#    - 1个神经元用于二分类输出
#    - activation='sigmoid'：将输出压缩为0到1之间的概率
model.add(Dense(1, activation='sigmoid'))# 5. 编译模型
#    - loss='binary_crossentropy'：用于二分类
#    - optimizer='adam'：一种流行且有效的优化算法
#    - metrics=['accuracy']：训练期间跟踪性能
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])print("DNN模型创建并编译完成！")
model.summary() # 打印模型层的摘要

解释：

Sequential()：这为我们的神经网络创建了一个空白画布，可以一层一层地堆叠。
Dense(1024, input_dim=41, activation='relu')：这是我们的第一个主要处理层。它有1024个神经元。input_dim=41对于第一层至关重要，告诉Keras输入特征的大小。我们使用relu来学习非线性模式。
Dropout(0.01)：该层通过随机丢弃1%的神经元连接来防止过拟合。
Dense(1, activation='sigmoid')：这是最终的决策层。如第1章所述，对于二分类，我们使用1个神经元和sigmoid激活来输出概率（0到1）。
model.compile(...)：这为训练准备模型。loss='binary_crossentropy'测量预测与真实标签的差距。optimizer='adam'是调整权重以最小化损失的“引擎”。metrics=['accuracy']是我们跟踪模型表现的指标。

扩展到多层和多分类

为了使DNN“更深”（更多隐藏层），只需添加更多的Dense和Dropout层：

from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
# ...（数据准备如前所述）...# 多分类示例：假设 num_classes = 5（正常、DoS、Probe、R2L、U2R）
num_classes = 5
# y_train_dummy 应为 one-hot 编码，例如 to_categorical(y_train_raw, num_classes=5)model_deep = Sequential()
model_deep.add(Dense(1024, input_dim=41, activation='relu'))
model_deep.add(Dropout(0.01))
model_deep.add(Dense(768, activation='relu')) # 第二个隐藏层
model_deep.add(Dropout(0.01))
model_deep.add(Dense(512, activation='relu')) # 第三个隐藏层
model_deep.add(Dropout(0.01))
# ... 可以添加更多层 ...
model_deep.add(Dense(256, activation='relu')) # 第四个隐藏层
model_deep.add(Dropout(0.01))
model_deep.add(Dense(128, activation='relu')) # 第五个隐藏层
model_deep.add(Dropout(0.01))# 对于多分类（如第1章所述）：
model_deep.add(Dense(num_classes, activation='softmax'))model_deep.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])print("\n用于多分类的深度DNN模型创建并编译完成！")
model_deep.summary()

多分类的关键区别：

Dense(num_classes, activation='softmax')：输出层现在有num_classes（例如5）个神经元，softmax激活确保输出是每个类的概率，总和为1。
loss='categorical_crossentropy'：当标签是one-hot编码时（多分类问题中应该如此，如第1章所述），这是合适的损失函数。

幕后：DNN如何做决策

将DNN想象为一个流水线，信息（网络流量数据）在最终决策前经过多个阶段的精炼和处理。

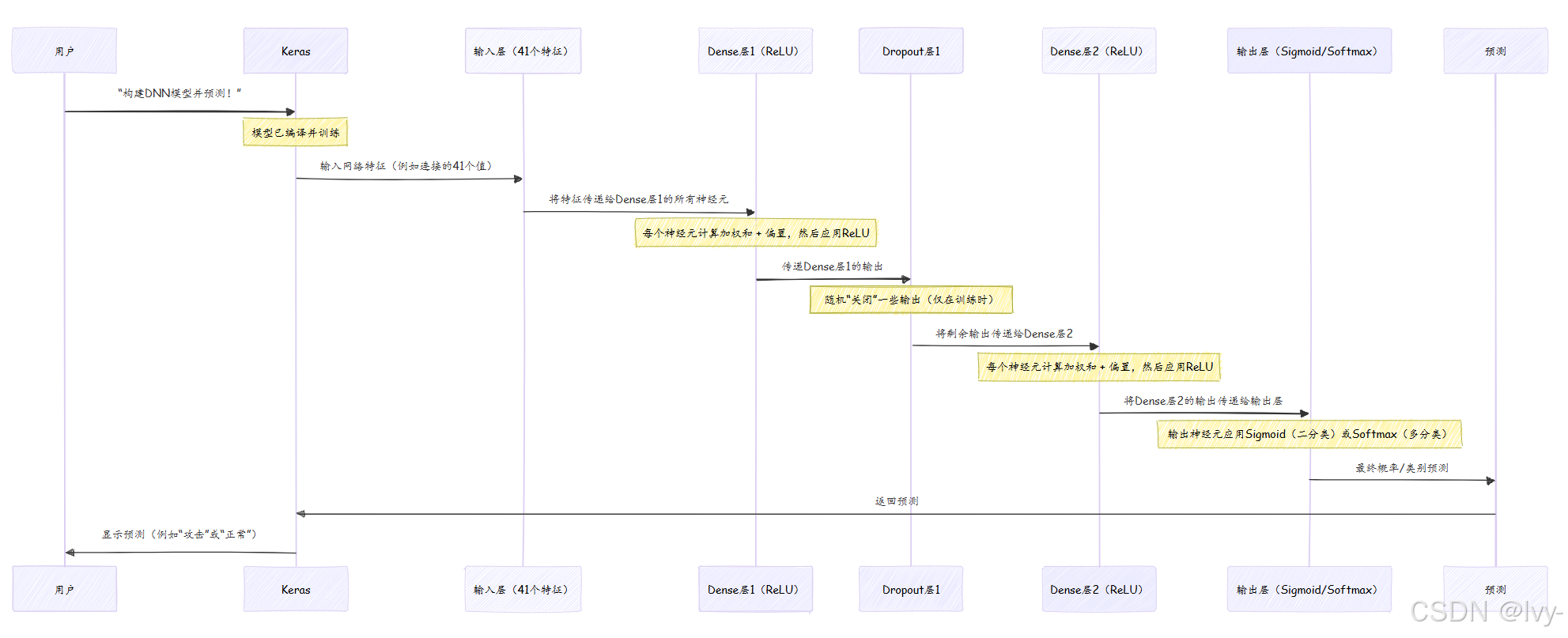
在这里插入图片描述

在训练期间（我们将在第8章：模型训练生命周期（Keras）中介绍），这个过程会反复进行。每次传递后，模型将其预测与真实标签进行比较，计算loss，然后微妙地调整每个Dense层中的所有权重和偏置，以减少下一次的loss。这种迭代调整就是模型“学习”的方式。

深入项目代码参考

让我们看看实际项目代码文件，了解DNN是如何实现的。你可以在KDDCup 99/dnn/文件夹（以及NSL-KDD、UNSW-NB15等其他数据集的类似文件夹）中找到这些内容。

1. 基本DNN（1个隐藏层）- 二分类

查看KDDCup 99/dnn/binary/dnn1.py或NSL-KDD/dnn/binary/dnn1.py。在数据加载和归一化步骤（类似于第2章）之后：

# 来自 KDDCup 99/dnn/binary/dnn1.py（简化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation# ...（X_train, y_train, X_test, y_test 已在此处准备好）...model = Sequential()
# 输入层（由第一个Dense层的input_dim隐式处理）
# 第一个隐藏层（Dense层1）
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01)) # 隐藏层后的Dropout
# 输出层（二分类1个神经元，sigmoid激活）
model.add(Dense(1))
model.add(Activation('sigmoid')) # 单独应用的激活函数model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（训练时的model.fit调用）...

观察：

input_dim=41用于指定数据集中的特征数量。
一个Dense层后跟一个Dropout层构成隐藏部分。
输出层使用Dense(1)和Activation('sigmoid')，与第1章中的二分类配置匹配。
binary_crossentropy是损失函数。

2. 更深DNN（5个隐藏层）- 二分类

现在，我们来看KDDCup 99/dnn/binary/dnn5.py。关键区别在于堆叠了多个Dense和Dropout层，使网络“更深”：

# 来自 KDDCup 99/dnn/binary/dnn5.py（简化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation# ...（X_train, y_train, X_test, y_test 已在此处准备好）...model = Sequential()
# 隐藏层1
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01))
# 隐藏层2
model.add(Dense(768, activation='relu'))
model.add(Dropout(0.01))
# 隐藏层3
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.01))
# 隐藏层4
model.add(Dense(256, activation='relu'))
model.add(Dropout(0.01))
# 隐藏层5
model.add(Dense(128, activation='relu'))
model.add(Dropout(0.01))
# 输出层
model.add(Dense(1))
model.add(Activation('sigmoid'))model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（训练时的model.fit调用）...

观察：

注意Dense和Dropout层的序列，每层的神经元数量比前一层少。这是一种常见的模式，逐步精炼特征。
输出层和编译（binary_crossentropy、sigmoid）保持不变，因为它仍然是二分类任务。

3. 多分类DNN（1个隐藏层）

最后，我们来看KDDCup 99/dnn/multiclass/dnn1.py。它使用与简单二分类DNN相同的网络结构，但适应了多分类：

# 来自 KDDCup 99/dnn/multiclass/dnn1.py（简化版）
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.utils.np_utils import to_categorical # 用于标签准备# ...（X_train, y_train1, X_test, y_test1 已在此处准备好）...
# 数据准备：对多分类标签进行one-hot编码
y_train = to_categorical(y_train1)
y_test = to_categorical(y_test1)model = Sequential()
# 隐藏层1
model.add(Dense(1024, input_dim=41, activation='relu'))
model.add(Dropout(0.01))
# 输出层（N个神经元对应N个类别，softmax激活）
# 假设5个类别（正常、DoS、Probe、R2L、U2R）
model.add(Dense(5)) # 5个神经元对应5个类别
model.add(Activation('softmax'))model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# ...（训练时的model.fit调用）...