深入理解算法效率——时间和空间复杂度详解

目录

一、引言：为什么我们需要分析算法效率？

二、算法效率的维度

2.1 时间复杂度（Time Complexity）

2.2 空间复杂度（Space Complexity）

三、深入理解算法时间复杂度

3.1 时间复杂度的基础概念

3.2 大O表示法 (Big O Notation)

3.3 最好、最坏与平均情况

四、常见时间复杂度计算与示例

4.1 O(1) - 常数时间复杂度

4.2 O(N) - 线性时间复杂度

4.3 O(N²) - 平方时间复杂度

4.4 O(logN) - 对数时间复杂度

4.5 O(2ᴺ) - 指数时间复杂度

五、空间复杂度分析

5.1 O(1) - 常数空间复杂度

5.2 O(N) - 线性空间复杂度

5.3 递归调用的空间复杂度

六、常见复杂度对比与可视化

七、总结

---

一、引言：为什么我们需要分析算法效率？

        在编程的世界中，我们常常需要用多种算法来解决同一个问题。例如，计算斐波那契数列可以使用递归方法

public static long Fib(int N) {if (N <= 2) return 1;return Fib(N - 1) + Fib(N - 2);
}

        这段代码虽然简洁，但是效率极低。当N的值较大时，程序运行时间程指数级增长，甚至可能导致栈溢出。

        为了科学衡量算法的优劣，我们引入了时间复杂度和空间复杂度的概念。

二、算法效率的维度

2.1 时间复杂度（Time Complexity）

衡量算法执行所需的时间，通常表示为输入规模的函数。我们关注的是随着输入规模的增大，算法执行时间的增长趋势，而非具体的执行时间。

2.2 空间复杂度（Space Complexity）

衡量算法执行过程中所需的额外内存空间。同样表示为输入规模的函数，关注内存使用量的增长趋势。

随着硬件技术的发展，存储空间成本大幅降低，时间复杂度往往成为我们更关注的指标。但在嵌入式系统或大数据处理场景中，空间复杂度仍然至关重要。

三、深入理解算法时间复杂度

3.1 时间复杂度的基础概念

算法的时间复杂度不是测量具体的执行时间，而是计算基本操作的执行次数。这是因为：

• 不同的硬件环境执行时间不同
• 不同的编程语言执行效率不同
• 不同的编译器优化程度不同

通过计算基本操作次数，我们可以得到与环境无关的算法效率衡量标准。

3.2 大O表示法 (Big O Notation)

大O表示法描述了算法的渐进行为，提供了复杂度分析的上界。推导方法为：

1. 用常数1取代运行时间中的所有加法常数
2. 在修改后的运行次数函数中，只保留最高阶项
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数

实际案例分析：

void func1(int N) {int count = 0;//第一个嵌套循环：N x N 次for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++:}}//第二个循环：2 x N 次for (int k = 0; k < 2*N; k++) {count++;}//第三个循环：10次int M = 10;while (M > 0) {count++;M--;}
}

该函数的总执行次数为：F(N) = N² + 2N + 10

使用大O表示法：

• 去除常数项：N² + 2N
• 只保留最高阶项：N²
• 去除系数：N²

因此，时间复杂度为 O(N²)

3.3 最好、最坏与平均情况

算法性能可能因输入数据的不同而变化：

• 最好情况：最小运行次数（下界）
• 最坏情况：最大运行次数（上界，通常我们关注这个）
• 平均情况：期望运行次数
   

示例：数组中查找元素

int findElement(int[] array, int target) {for (int i = 0; i < array.length; i++) {if (array[i] == target) {return i;}}return -1;
}

• 最好情况：目标元素在第一个位置 → O(1)
• 最坏情况：目标元素在最后或不存在 → O(N)
• 平均情况：目标元素在中间某位置 → O(N/2) → 简化为 O(N)
   

在实际分析中，我们通常关注最坏情况，因为这提供了算法性能的保证。

四、常见时间复杂度计算与示例

4.1 O(1) - 常数时间复杂度

void func1(int N) {int count = 0;for (int i = 0; i < 100; i++) {count++;}System.out.println(count);
}

无论输入规模N多大，执行次数都是100次，因此是O(1)

4.2 O(N) - 线性时间复杂度

void func2(int N) {int count = 0;for (int i = 0; i < 2*N; i++) {count++;}int M = 10;while (M > 0) {count++;M--;}System.out.println(count);
}

执行次数是2N+10，简化后是O(N)

4.3 O(N²) - 平方时间复杂度

void bubbleSort(int[] array) {for (int i = 0; i < array.length-1; i++) {boolean sorted = true;for (int j = 0; j < array.length-1-i; j++) {if (array[j] > array[i]) {int temp = array[j];array[j] = array[i];array[i] = temp;sorted = false;}}if (sorted == true) {break;}}
}

最坏情况下需要执行 (N-1) + (N-2) + ... + 1 = N(N-1)/2 次操作，简化后为 O(N²)。

4.4 O(logN) - 对数时间复杂度

int binarySearch(int[] array, int val) {int left = 0;int right = array.length - 1;while (left <= right) {int mid = (left+right) / 2;if (array[mid] > val) {right = mid - 1;} else if (array[mid] < val) {left = mid + 1;} else {return mid;}}return -1;
}

二分查找每次将搜索范围减半，因此时间复杂度是 O(logN)。

直观理解对数复杂度：假设有一张纸，每次将其对折，问对折多少次后厚度会超过一定高度？这就是对数函数的增长模式。

4.5 O(2ᴺ) - 指数时间复杂度

int fibanacci(int N) {return N<2 ? N : fibanacci(N-1)+fibanacci(N-2);
}

递归计算斐波那契数列会形成一颗深度为N的二叉树，节点数约为2ᴺ，因此时间复杂度为 O(2ᴺ)。

五、空间复杂度分析

空间复杂度衡量算法运行过程中临时占用的存储空间大小（不包括输入数据本身占用的空间）。

5.1 O(1) - 常数空间复杂度

void bubbleSort(int[] array) {    //仅使用常数个额外变量：i、j和sortedfor (int i = 0; i < array.length-1; i++) {boolean sorted = true;for (int j = 0; j < array.length-1-i; j++) {if (array[j] > array[i]) {int temp = array[j];array[j] = array[i];array[i] = temp;sorted = false;}}if (sorted == true) {break;}}
}

只使用了end、sorted、i等常数个变量，空间复杂度为 O(1)。

5.2 O(N) - 线性空间复杂度

int[] fibonacci(int N) {int[] fibArray = new long int[N+1];fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= N; i++) {fibArray[i] = fibArray[i-1] + fibArray[i-2];}return fibArray;
}

创建了长度为n+1的数组，空间复杂度为 O(N)。

5.3 递归调用的空间复杂度

long factorial(int N) {return N<2 ? N : factorial(N-1)*N;
}

每次递归调用都会在调用栈上创建一个新的栈帧，递归深度为N，因此空间复杂度为 O(N)。

注意：递归算法的空间复杂度与递归深度相关，这可能成为限制算法实用性的因素。

六、常见复杂度对比与可视化

复杂度	增长趋势
O(1)	恒定
O(logN)	缓慢增长
O(N)	线性增长
O(NlogN)	接近线性
O(N²)	快速增长
O(2ᴺ)	爆发式增长

以下图片可直观体现各个复杂度的优劣：

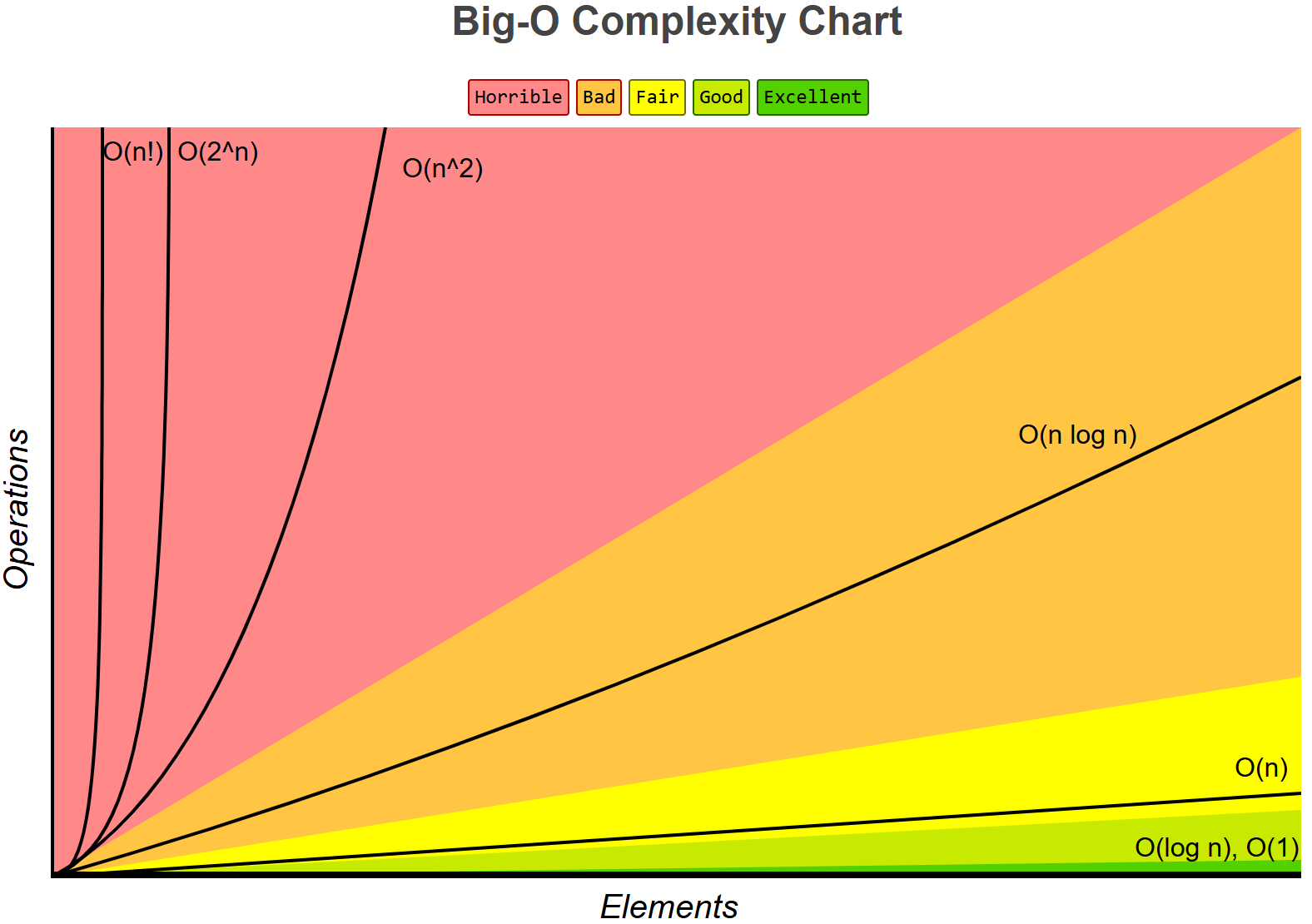
七、总结

时间复杂度和空间复杂度是算法分析的核心概念，它们帮助我们：

1. 客观评价算法效率，不受具体硬件环境影响
2. 预测算法在不同规模输入下的性能表现
3. 在算法设计中做出合理的权衡决策
4. 为算法优化提供方向和目标

掌握复杂度分析不仅有助于编写高效代码，也是技术面试中必备的技能。通过理解各种常见算法的复杂度特征，我们能够更好地选择和应用合适的算法解决实际问题。

---

完