人工智能中的线性代数总结--简单篇

numpy库中的dot函数来计算矩阵和向量的点积

def matrix_vector_dot_product(a, b):import numpy as npif (len(a[0]) != len(b)):return -1# 使用tolist()将结果转换为列表return np.dot(a, b).tolist()

原始方法

def matrix_vector_dot_product(matrix, vector):if len(matrix[0]) != len(vector):return -1l = []for i in matrix:num = 0for j in range(len(i)):num += (i[j]*vector[j])l.append(num)return l# 主程序
if __name__ == "__main__":# 输入矩阵和向量matrix_input = input()vector_input = input()# 处理输入import astmatrix = ast.literal_eval(matrix_input)vector = ast.literal_eval(vector_input)# 调用函数计算点积output = matrix_vector_dot_product(matrix, vector)# 输出结果print(output)

numpy库中给定的矩阵 A，其转置矩阵表示为 A^T

def transpose_matrix(a: List[List[Union[int, float]]]) -> List[List[Union[int, float]]]:import numpy as npreturn np.array(a).T.tolist()

使用numpy库的reshape方法矩阵重塑

矩阵重塑是将一个矩阵转换为另一个形状的过程，前提是新形状的元素总数与原矩阵相同

def reshape_matrix(a: List[List[Union[int, float]]], new_shape: Tuple[int, int]) -> List[List[Union[int, float]]]:import numpy as npif len(a) * len(a[0]) != new_shape[0] * new_shape[1]:return -1return np.array(a).reshape(new_shape).tolist()

使用numpy库的mean方法按行或列计算平均值

def calculate_matrix_mean(matrix: List[List[Union[int, float]]], mode: str) -> List[float]:import numpy as npif mode == 'column':return np.mean(matrix, axis=0).tolist()elif mode == 'row':return np.mean(matrix, axis=1).tolist()else:raise ValueError("Mode must be 'row' or 'column'")

使用python的广播机制进行标量的矩阵乘法

def scalar_multiply(matrix: List[List[Union[int, float]]], scalar: Union[int, float]) -> List[List[Union[int, float]]]:import numpy as npreturn (np.array(matrix) * scalar).tolist()

使用numpy库的cov方法计算协方差矩阵

协方差矩阵是一种描述两个随机变量之间关系的矩阵，其计算公式为：

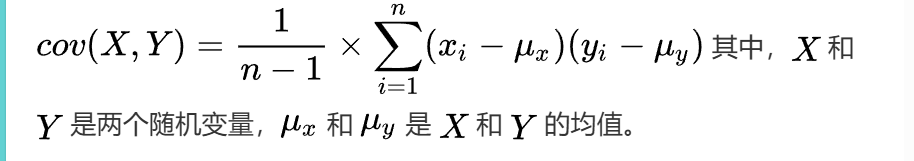
import numpy as npdef jia(vectors, a):return [i + a for i in vectors]def dianji(a,b):if len(a) != len(b):return -1s = 0for j in range(len(a)):s += a[j] * b[j]return sdef cov(x,y):return dianji(jia(x, -sum(x)/len(x)),jia(y, -sum(y)/len(y))) / (len(x)-1)def calculate_covariance_matrix(vectors):# 补全代码return [[cov(x,y) for x in vectors] for y in vectors]# 主程序
if __name__ == "__main__":# 输入ndarrayA = input()# 处理输入import astA = ast.literal_eval(ndarrayA)# 调用函数计算output = calculate_covariance_matrix(A)# 输出结果print(output)

原始方法

import numpy as npdef calculate_covariance_matrix(vectors):n_features = len(vectors)n_observations = len(vectors[0])covariance_matrix = np.zeros([n_features, n_features])means = [sum(feature) / n_observations for feature in vectors]for i in range(n_features):for j in range(i, n_features):covariance = sum((vectors[i][k] - means[i]) * (vectors[j][k] - means[j])for k in range(n_observations)) / (n_observations - 1)covariance_matrix[i][j] = covariance_matrix[j][i] = covariancereturn covariance_matrix.tolist()
# 主程序
if __name__ == "__main__":# 输入ndarrayA = input()# 处理输入import astA = ast.literal_eval(ndarrayA)# 调用函数计算output = calculate_covariance_matrix(A)# 输出结果print(output)

基向量变换矩阵

基向量变换矩阵（Basis Vector Transformation Matrix）是一种常用的矩阵，用于将基向量变换为另一个基向量。

import numpy as npdef transform_basis(B, C):B = np.array(B)C = np.array(C)C = np.linalg.inv(C)P = B@Creturn P.tolist()if __name__ == "__main__":B = np.array(eval(input()))C = np.array(eval(input()))print(transform_basis(B, C))

 将向量转换为对角矩阵

def make_diagonal(x):identity_matrix = np.identity(np.size(x))return (identity_matrix*x)

原始方法

def make_diagonal(x):x = np.array(x)zeros = np.zeros((len(x),len(x)),dtype=np.float16)for i in range(len(x)):zeros[i,i]=x[i]return zerosif __name__ == "__main__":x = np.array(eval(input()))print(make_diagonal(x))

实现压缩行稀疏矩阵（CSR）格式转换

压缩行稀疏矩阵（CSR）格式是一种特殊的矩阵存储格式，其特点是只存储非零元素的值、行号和列指针。本质上是一种三元组表示法。

输入

[[1, 0, 0], [2, 3, 0], [0, 4, 5]]

输出

[1, 2, 3, 4, 5]
[0, 0, 1, 1, 2]
[0, 1, 3, 5]

def compressed_row_sparse_matrix(dense_matrix):vals = []col_idx = []row_ptr=[0]for x in dense_matrix:for i,y in enumerate(x):if y!=0:vals.append(y)col_idx.append(i)row_ptr.append(len(vals))return vals, col_idx, row_ptrif __name__ == "__main__":dense_matrix = eval(input())vals, col_idx, row_ptr = compressed_row_sparse_matrix(dense_matrix)print(vals)print(col_idx)print(row_ptr)

实现向量到直线的正交投影

def orthogonal_projection(v, L):import numpy as npv = np.array(v)L = np.array(L)a = (((v@L)/np.dot(L,L))*L)a = a.tolist()return aif __name__ == "__main__":v = eval(input())L = eval(input())print(orthogonal_projection(v, L))

实现压缩列稀疏矩阵

def compressed_col_sparse_matrix(dense_matrix):from scipy.sparse import csc_matrixsparse = csc_matrix(dense_matrix)return sparse.data.tolist(), sparse.indices.tolist(), sparse.indptr.tolist()

原始方法

def compressed_col_sparse_matrix(dense_matrix):vals, row_idx, col_ptr = [],[],[0]import numpy as npdense_matrix = np.array(dense_matrix)dense_matrix = dense_matrix.Tfor i in dense_matrix:for j,x in enumerate(i):if x!=0:vals.append(x)row_idx.append(j)col_ptr.append(len(vals))return vals, row_idx, col_ptrif __name__ == "__main__":dense_matrix = eval(input())vals, row_idx, col_ptr = compressed_col_sparse_matrix(dense_matrix)print(vals)print(row_idx)print(col_ptr)

计算向量之间的余弦相似度

import numpy as npdef cosine_similarity(v1, v2):# Implement your code hereif v1.shape != v2.shape:raise ValueError("Arrays must have the same shape")if v1.size == 0:raise ValueError("Arrays cannot be empty")v1 = v1.flatten()v2 = v2.flatten()val= (v1@v2)/(np.sqrt(np.dot(v1,v1))*np.sqrt(np.dot(v2,v2)))return round(val, 3)if __name__ == "__main__":v1 = np.array(eval(input()))v2 = np.array(eval(input()))print(cosine_similarity(v1, v2))

泊松分布概率计算器

泊松分布是一种描述随机事件发生次数的概率分布，其计算公式为：

import mathdef poisson_probability(k, lam):# Your code hereo=(math.exp(-lam))*(lam**k)u=math.factorial(k)val=o/ureturn round(val, 5)if __name__ == "__main__":k, lam = map(int, input().split())print(poisson_probability(k, lam))