磁共振成像原理（理论）：信号产生和探测（3）

下面是磁共振成像原理（理论）部分的主要内容，请按照顺序阅读

1. [[信号产生和探测]]，包括基本物理原理
2. [[信号的特征]]，包括自由感应衰减FID，射频回波，梯度回波等
3. [[信号定位]]，包括选层，频率编码，相位编码以及K空间
4. [[图像重建]]
5. [[图像对比度]]
6. [[图像分辨率，噪声和伪影]]
7. [[快速扫描成像介绍]]

本篇主要介绍信号的产生和探测。这是第三部分，布洛赫方程。

布洛赫方程 （Bloch Equation）

布洛赫方程的一般形式如下：
$$\frac{d\vec{M}}{dt}=\gamma \vec{M}\times \vec{B}-\frac{M_x\vec{i}+M_y\vec{j}}{T_2}-\frac{(M_z-M_z^0)\vec{k}}{T_1}\text{\hspace{1em}(3.69)}$$
上式中，$M_z^0$ 是宏观磁化强度$\vec{M}$ 在外磁场$B_0$ 的作用下的热平衡态幅值，请参考式子（3.39）， 分别是横向和纵向弛豫时间，表示被扰动后恢复热平衡态的时间常数；一般来说射频脉冲时间远小于 $T_1,T_2$ ，所以在射频脉冲作用期间，我们忽略弛豫的影响，所以式子（3.69）可以进一步被简化：
$$\frac{d\vec{M}}{dt}=\gamma \vec{M}\times \vec{B}\text{\hspace{1em}(3.70)}$$
大家可能会注意到，这个式子和式子（3.15）$\frac{d\vec{\mu }}{dt}=\gamma \vec{\mu }\times B_0\vec{k}$ 很接近，在这里将式子（3.67）代入到（3.70）中，可以得到：
$$\frac{\partial {\vec{M}}_{\text{rot}}}{\partial t}=\gamma {\vec{M}}_{\text{rot}}\times {\vec{B}}_{\text{eff}}\text{\hspace{1em}(3.72)}$$
其中
$${\vec{B}}_{\text{eff}}={\vec{B}}_{\text{rot}}+\frac{\vec{\omega }}{\gamma }\text{\hspace{1em}(3.73)}$$
有效磁场${\vec{B}}_{\text{eff}}$ 表示宏观磁化强度在旋转坐标系下“感受到”的磁场。当$\vec{B}=B_0\vec{k}$ ，同时 $\vec{\omega }=-\gamma B_0\vec{k}$ ，所以在仅有$B_0$时，系统终会恢复到热平衡态，此时宏观磁化强度的变化率为0.
$${\vec{B}}_{\text{eff}}={\vec{B}}_{\text{rot}}-\frac{\gamma B_0\vec{k}}{\gamma }=B_0\vec{k}-B_0\vec{k}=0\text{\hspace{1em}(3.74)}$$

共振激发 On-Resonance Excitations

回顾式子（3.50）${\vec{B}}_1(t)=B_1^e(t)[\cos ({\omega }_{\mathrm{rf}}t+\phi )\vec{i}-\sin ({\omega }_{\mathrm{rf}}t+\phi )\vec{j}]$，此时的射频频率时$w_{rf}$ ，设初始相位为0，对其应用旋转变换(3.63)
$${\vec{B}}_{1,rot}=\left[\begin{array}{cc}\cos \omega t& -\sin \omega t\\ \sin \omega t& \cos \omega t\end{array}\right]{\vec{B}}_1(t)=B_1^e(t)\left[\begin{array}{cc}\cos \omega t& -\sin \omega t\\ \sin \omega t& \cos \omega t\end{array}\right]\left[\begin{array}{c}\cos ({\omega }_{\mathrm{rf}})\\ -\sin ({\omega }_{\mathrm{rf}}t)\end{array}\right]$$
化简可得
$${\vec{B}}_{1,rot}=B_1^e(t)\left[\begin{array}{c}1\\ 0\end{array}\right]$$
即
$${\vec{B}}_{1,rot}=B_1^e(t)\overrightarrow{i^{\prime }}\text{\hspace{1em}(3.76)}$$

式子（3.73）可得旋转坐标下等效磁场，将射频场页考虑在里面后，得到：
$${\vec{B}}_{eff}=B_0\overrightarrow{k^{\prime }}+B_1^e(t)\overrightarrow{i^{\prime }}+\frac{{\vec{\omega }}_{rf}}{\gamma }$$
$${\vec{B}}_{eff}=\left(B_0-\frac{{\omega }_{\text{rf}}}{\gamma }\right){\vec{k}}^{\prime }+B_1^e(t){\vec{i}}^{\prime }\text{\hspace{1em}(3.77)}$$
这里近一步引入共振激发条件，
$$w_{rf}=w_0=\gamma B_0\text{\hspace{1em}(3.78)}$$
然后得到：
$${\vec{B}}_{\text{eff}}=B_1^e(t){\vec{i}}^{\prime }\text{\hspace{1em}(3.79)}$$
将其代入式子（3.72），得：
$$\frac{\partial {\vec{M}}_{\text{rot}}}{\partial t}=\gamma {\vec{M}}_{\text{rot}}\times {\vec{B}}_{\text{eff}}=\gamma {\vec{M}}_{\text{rot}}\times B_1^e(t){\vec{i}}^{\prime }\text{\hspace{1em}(3.72)}$$
矢量的外积，满足
$$\{\begin{array}{l}\vec{j}\times \vec{k}=\vec{i}\\ \vec{i}\times \vec{k}=-\vec{j}\\ \vec{k}\times \vec{k}=\vec{0}\end{array}$$
分别对 ${\vec{i}}^{\prime },{\vec{j}}^{\prime },{\vec{k}}^{\prime }$ 三个方向单独求解，可得
$$\{\begin{array}{l}\frac{d{M}_{x^{\prime }}}{dt}=0\\ \frac{d{M}_{y^{\prime }}}{dt}=\gamma B_1^e(t)M_{z^{\prime }}\\ \frac{d{M}_{z^{\prime }}}{dt}=-\gamma B_1^e(t)M_{y^{\prime }}\end{array}\text{\hspace{1em}(3.81)}$$
引入初始化条件 $M_{x^{\prime }}=M_{y^{\prime }}=0,M_{z^{\prime }}=M_z^0$ ，可解得：
$$\{\begin{array}{l}{M}_{x^{\prime }}(t)=0\\ M_{y^{\prime }}(t)=M_z^0\sin \left({\int }_0^t\gamma B_1^e(\hat{t})d\hat{t}\right)\\ M_{z^{\prime }}(t)=M_z^0\cos \left({\int }_0^t\gamma B_1^e(\hat{t})d\hat{t}\right)\end{array}(0\le t\le {\tau }_p)\text{\hspace{1em}(3.82)}$$

可以看到，沿着实验室坐标系 $x$ 方向的线性偏振射频场(3.48)，它可以等效成一个圆偏振（3.50）。它在旋转坐标系下的等效磁场(3.76)，是 $x^{\prime }$方向的，因此它不会对$x^{\prime }$方向的宏观磁化分量 $M_{x^{\prime }}$有影响（同向矢量外积为0），而是对$M_{y^{\prime }}，M_{z^{\prime }}$有影响。

当射频信号的包络是矩形波时：
$$B_1^e(t)=B_1\Pi \left(\frac{t-{\tau }_p/2}{{\tau }_p}\right)\text{\hspace{1em}(3.83)}$$
此时 (3.82) 变成：

$$\{\begin{array}{rl}{M}_{x^{\prime }}(t)& =0\\ M_{y^{\prime }}(t)& =M_z^0\sin ({\omega }_{1}t)0\le t\le {\tau }_p\\ M_{z^{\prime }}(t)& =M_z^0\cos ({\omega }_{1}t)\end{array}\text{\hspace{1em}(3.84)}$$

此时
$${\vec{\omega }}_1=-\gamma {\vec{B}}_1\text{\hspace{1em}(3.85)}$$

可以看到，在此射频场的激发下：

1. 如果在旋转坐标下下去观察，${\vec{M}}_{rot}$ 是以$x^{\prime }$为轴在旋转，下图左。这也是为什么，我们需要建立旋转坐标系，因为在旋转坐标系下，很多现象会变得直接直观容易理解。
2. 如果在实验室坐标下去观察，$\vec{M}$ 是以绕着$z$ 轴旋转的同时，也绕着$x$为轴在进动（precession），下图右
   

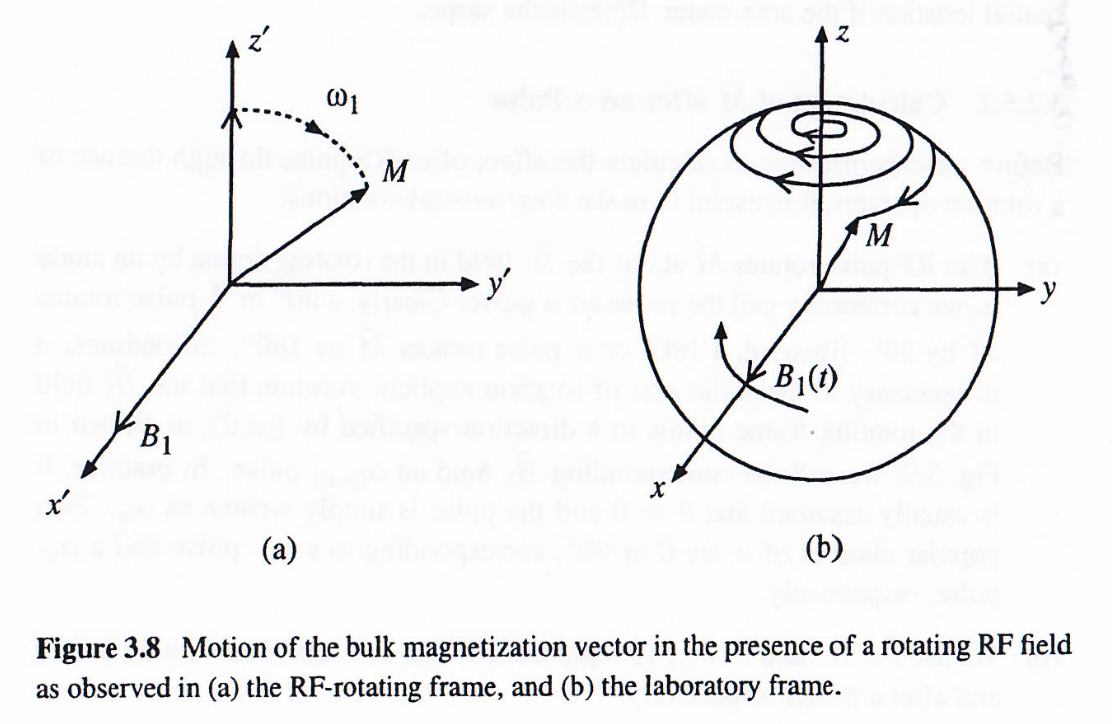
在仅有外部静态磁场${\vec{B}}_0$时，且当系统处于热平衡时，宏观磁化强度$\vec{M}$在 $x,y$上的相互抵消，仅表现出$z$方向的分量。即使在旋转坐标系中中去观察，${\vec{M}}_{rot}$ 也仅余下$z^{\prime }$ 方向的分量。当存在外部的射频场时，且满足共振条件，就会使得宏观磁化${\vec{M}}_{rot}$ 绕着 $x^{\prime }$ 旋转。这使得${\vec{M}}_{rot}$ 的$z^{\prime }$ 方向的分量逐渐翻转到$x^{\prime }{y}^{\prime }$平面（见式（3.84））。这个翻转角度 $\alpha$ 决定了翻转量：
$$\alpha ={\int }_0^{{\tau }_p}{\omega }_1(t)dt={\int }_0^{{\tau }_p}\gamma B_1^e(t)dt\text{\hspace{1em}(3.86)}$$

对于矩形波而言，翻转角度和射频激发时间时线性关系的：
$$\alpha ={\omega }_1{\tau }_p=\gamma B_1{\tau }_p\text{\hspace{1em}(3.87)}$$
举个例子，对质子而言，当${\tau }_p=0.1ms,B_1=0.6G$ 时，翻转角度 $\alpha =\frac{\pi }{2}$， 此时恰好可以把$M_z^0$ 全部翻转为 $M_{y^{\prime }}(t)$ (将$\alpha =\frac{\pi }{2}$ 代入式3.84)。

积分复现性初涉 （Reproducibility）

同时我们也需要注意到，翻转角度 $\alpha$ 同时取决于射频场的幅度以及激发持续时间， 同时需要注意到（见式3.86），$B_1^e(t)$ 包络的形状并不重要，重要的是包络下的面积。也就是说，不同的包络会让上述翻转有不同的轨迹，但是当脉冲结束后的停留位置（翻转角度）是一样的，只要包络面积相同。这就是功放设备对射频场和梯度场的一个重要的需求，也就是积分复现性，即要求在扫描期间，让射频场和梯度场的包络面积具备一定的重复性。

下面看一下，射频场 $\alpha$ 脉冲激发后的宏观强化矢量 $\vec{M}$ 如何计算。开始前，我们介绍一套符号：

1. 用 ${\alpha }_{x^{\prime }}$ 表示沿着旋转坐标系 $x^{\prime }$ 方向的射频脉冲， ${\alpha }_{y^{\prime }}$，${\alpha }_{z^{\prime }}$ 表示 $y^{\prime },z^{\prime }$ 方向的射频脉冲。
2. 用 $t=0_{-},t=0_{+}$ 表示射频脉冲前后时刻
3. 用 $\to$ 表示通用的自旋进动操作

下面举个例子：
$$M_{x^{\prime }}(0_{-})\stackrel{{\alpha }_{x^{\prime }}}{\to }{M}_{x^{\prime }}(0_{+})\text{\hspace{1em}(3.88)}$$
它表示，一个 ${\alpha }_{x^{\prime }}$ 脉冲让$M_{x^{\prime }}(0_{-})$ 变成 $M_{x^{\prime }}(0_{+})$

基于公式（3.82），用$\alpha$ 来代替积分后，得到热平衡后的变换关系，此时$M_{x^{\prime }}(0_{-})=0$，$M_{y^{\prime }}(0_{-})=0$
$$\{\begin{array}{l}{M}_{x^{\prime }}(0_{+})=0\\ M_{y^{\prime }}(0_{+})=M_z^0\sin \alpha \\ M_{z^{\prime }}(0_{+})=M_z^0\cos \alpha \end{array}\text{\hspace{1em}(3.89)}$$
而更通用的是非热平衡下的射频激发引入的变换
$$\{\begin{array}{l}{M}_{x^{\prime }}(0_{+})=M_{x^{\prime }}(0_{-})\\ M_{y^{\prime }}(0_{+})=M_{y^{\prime }}(0_{-})\cos \alpha +M_{z^{\prime }}(0_{-})\sin \alpha \\ M_{z^{\prime }}(0_{+})=-M_{y^{\prime }}(0_{-})\sin \alpha +M_{z^{\prime }}(0_{-})\cos \alpha \end{array}\text{\hspace{1em}(3.90)}$$
之前定义的都是$x^{\prime }$方向的，我们用更加紧凑的旋转操作矩阵形式来表示变换关系，不同轴分别是：
$x^{\prime }$方向：
$$R_{x^{\prime }}(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& -\sin \alpha & \cos \alpha \end{array}\right]\text{\hspace{1em}(3.91)}$$
$y^{\prime }$方向
$$R_{y^{\prime }}(\alpha )=\left[\begin{array}{ccc}\cos \alpha & 0& -\sin \alpha \\ 0& 1& 0\\ \sin \alpha & 0& \cos \alpha \end{array}\right]\text{\hspace{1em}(3.92)}$$
$z^{\prime }$方向
$$R_{z^{\prime }}(\alpha )=\left[\begin{array}{ccc}\cos \alpha & \sin \alpha & 0\\ -\sin \alpha & \cos \alpha & 0\\ 0& 0& 1\end{array}\right]\text{\hspace{1em}(3.93)}$$

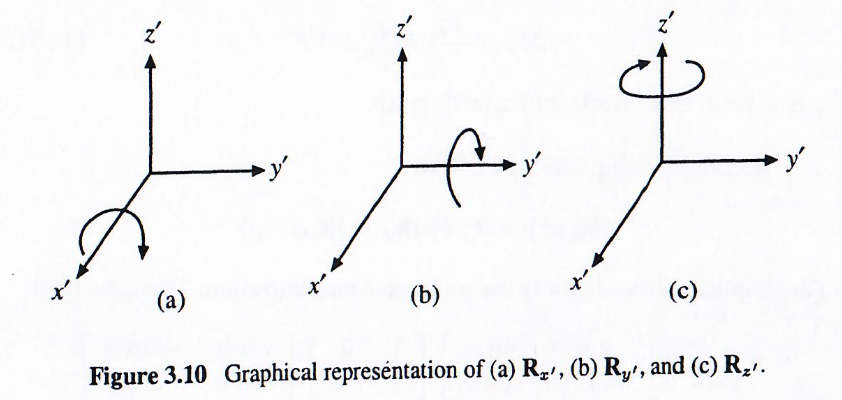
下面用矩阵来展示沿着 $x^{\prime },y^{\prime }$ 方向的射频脉冲对宏观磁化矢量的变换计算，注意是旋转坐标系下。
$${\vec{M}}_{\text{rot}}\left(0_{+}\right)\stackrel{{\alpha }_{x^{\prime }}}{\to }{\mathbf{R}}_{x^{\prime }}(\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)\text{\hspace{1em}(3.94a)}$$
$${\vec{M}}_{\text{rot}}\left(0_{+}\right)\stackrel{{\alpha }_{-x^{\prime }}}{\to }{\mathbf{R}}_{-x^{\prime }}(\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)={\mathbf{R}}_{x^{\prime }}(-\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)\text{\hspace{1em}(3.94b)}$$
$${\vec{M}}_{\text{rot}}\left(0_{+}\right)\stackrel{{\alpha }_{y^{\prime }}}{\to }{\mathbf{R}}_{y^{\prime }}(\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)\text{\hspace{1em}(3.94c)}$$
$${\vec{M}}_{\text{rot}}\left(0_{+}\right)\stackrel{{\alpha }_{-y^{\prime }}}{\to }{\mathbf{R}}_{-y^{\prime }}(\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)={\mathbf{R}}_{y^{\prime }}(-\alpha ){\vec{M}}_{\text{rot}}\left(0_{-}\right)\text{\hspace{1em}(3.94d)}$$
而沿着$x^{\prime }{y}^{\prime }$ 平面（和$x^{\prime }$的夹角为$\phi$）的任意射频脉冲，则不能直接把它分解成$x^{\prime },y^{\prime }$ 两个变换的叠加。而应该用：

1. 将旋转坐标系的$x^{\prime }$轴，沿着$z^{\prime }$轴旋转$-\phi$，旋转后使得$x^{\prime }$轴和射频同向------$R_{z^{\prime }}(-\phi )$
2. 此时再利用${\alpha }_{x^{\prime }}$完成激发变换------$R_{x^{\prime }}(\alpha )$
3. 将旋转坐标系的$x^{\prime }$轴，沿着$z^{\prime }$轴旋转$\phi$恢复第一步的变换------$R_{z^{\prime }}(\phi )$
   $${\vec{M}}_{\text{rot}}(0_{+})=R_{z^{\prime }}(\phi )R_{x^{\prime }}(\alpha )R_{z^{\prime }}(-\phi ){\vec{M}}_{\text{rot}}(0_{-})\text{\hspace{1em}(3.95)}$$