运筹学——对偶问题的建模，以及它的基本性质

对偶问题的建模

例如，一个资源配置型线性规划问题，A厂要向B厂租设备，A希望价格越低越好，B希望越高越好，这个是一个贴合生活的实际问题，那么租金应该是至少要高于B厂自己使用时的获利。
从A的角度列目标函数是求min，并且约束方程是≤决策变量，从B的角度列目标函数就是求max，并且约束方程是≥决策变量，这两组方程就构成了一个对偶问题。

例如，一个线性规划问题如下所示：

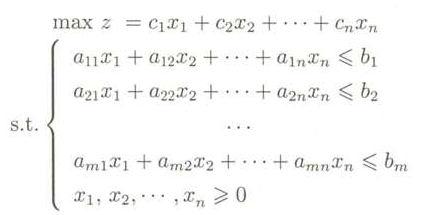
它的对偶问题：

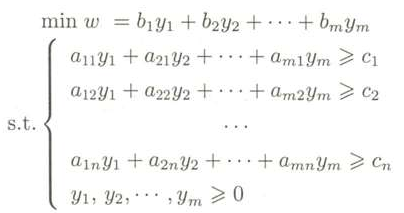
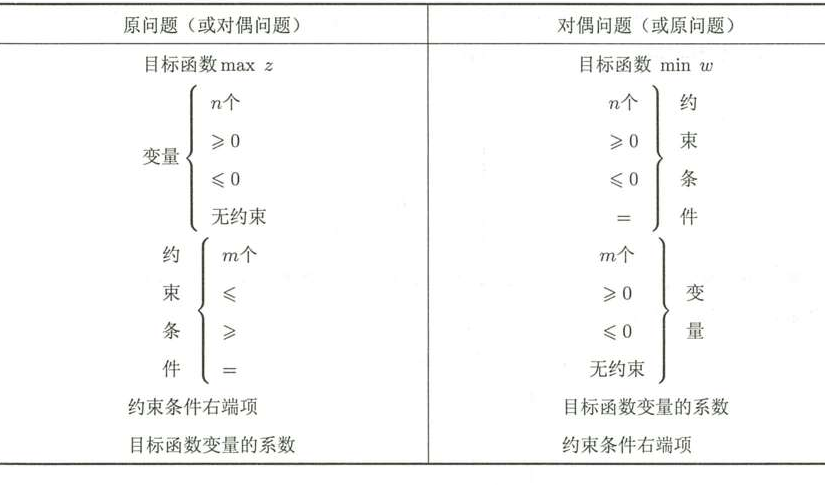
仔细观察他们之间的关系就会发现以下几个特点：

1，原问题目标函数中的c_i变成了对偶问题的决策项，相应的原问题的决策项变为了对偶问题目标函数中的c_i，是互相变的，因此，原问题决策变量的个数决定对偶问题的约束条件个数。
2，原问题的系数矩阵A在经过转置之后变为对偶问题的系数矩阵A’，就是A’ =A^T。
3，原问题求max，对偶问题求min。
4，原问题中的约束条件若是≤，对偶问题中的约束条件就是≥。

用矩阵形式表示原问题与对偶问题：

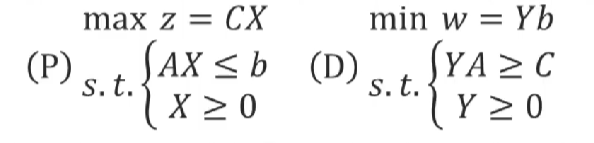
原问题中X为一个列向量，对偶问题中Y是一个行向量

特殊情况

当约束条件有等号时，如下图所示的这种线性规划问题：

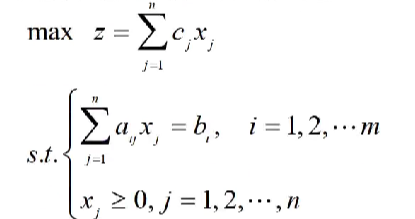
由于ax=b——>ax≥b，且 ax≤b
因此，可以把等式拆分为两个不等式同时成立。
又由于这是求max的问题，所以把≥转换为≤号，也就是两边同时乘以 -1 即可，此时就有以下这样的约束条件：

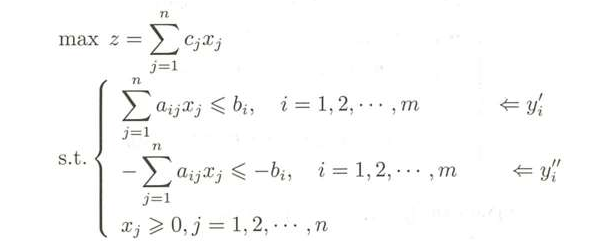
假设y’ 对应第一组约束的对偶变量，y"对应第二组对偶变量，那么该线性规划问题的对偶问题就是：

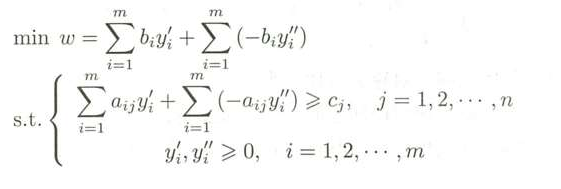
整理就得：

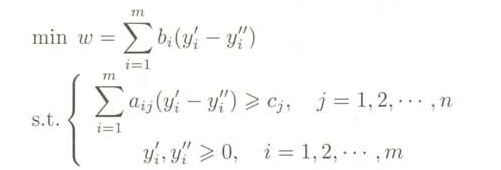
此时，令 y=y’- y"， y’，y" ≥0，就有：

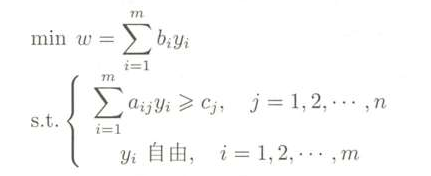
若原问题的约束条件是等号，那么对应的对偶问题的决策条件就是自由变量。

对比这组对偶问题的不等式符号，原问题中约束条件的符号与对偶问题决策变量的符号相反，原问题的决策变量的符号与对偶问题的约束条件符号相同。

举个栗子🌰练一下手
如下图所示的线性规划问题，写出它的对偶问题。

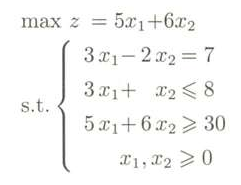
先自己尝试着写一遍哦~~

解析：

因为约束条件中包含等式和≥，所以先将约束条件进行变换：

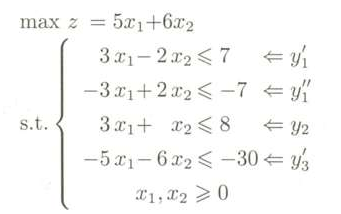
将每个对应的对偶问题记为y₁’,y₁",y₂,y₃,写出对偶变量：

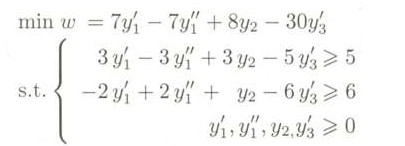
令y₁=y₁’ - y₁",y₃=- y₃’,整理就得：

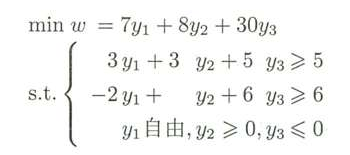
结论

对偶问题的基本性质

1，对称性：
对偶问题的对偶是原问题。
2，弱对偶性：
原问题是求max，对偶问题是求min时，若X是原问题的可行解，Y是对偶问题的可行解，那么存在CX≤Yb.
3，最优性：
若X,Y是原问题和对偶问题的可行解，且有CX=Yb，那么它们分别是原问题和对偶问题的最优解。
4，最优对偶解;
若B是原问题的最优基，那么Y=C_B ✖️ B^-1，也就是Y为对偶问题的最优解。

也就是说Y对应的就是在初始单纯形表中，单位矩阵的位置所对应的决策变量在最优单纯形表中检验系数的相反数。
看图理解

5，互补松弛性
若X,Y分别是原问题和对偶问题的可行解，

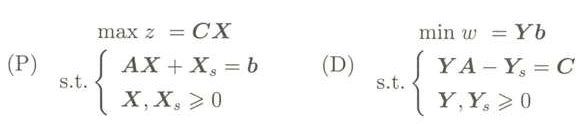
那么X,Y是这两个问题的最优解的充分必要条件是：

这个性质表明在资源配置问题中，当资源有剩余时，它的对偶解一定是0。反之，若某个资源对应的对偶解取值为正时，该资源一定对应与系统的瓶颈资源。

未完待更~~~

：）