从零开始构建图注意力网络:GAT算法原理与数值实现详解
图数据在机器学习中的地位越来越重要。社交网络的用户关系、论文引用网络、分子结构,这些都不是传统的表格或序列数据能很好处理的。现实世界中实体之间的连接往往承载着关键信息。
图神经网络(GNN)的出现解决了这个问题,它让每个节点可以从邻居那里获取信息来更新自己的表示。图卷积网络(GCN)是其中的经典代表,但GCN有个明显的限制:所有邻居节点的贡献都是相等的(在归一化之后)。
这个假设在很多情况下并不合理。比如在社交网络中,不同朋友对你的影响程度肯定不一样;在分子中,也不是所有原子对化学性质的贡献都相同。
图注意力网络(GAT)就是为了解决这个问题而设计的。它引入注意力机制,让模型自己学会给不同邻居分配不同的权重,而不是简单地平均处理。用一个比喻来说,GCN像是"听取所有朋友的建议然后求平均",而GAT更像是"重点听那些真正懂行的朋友的话"。
本文文会详细拆解GAT的工作机制,用一个具体的4节点图例来演示整个计算过程。如果你读过原论文觉得数学公式比较抽象,这里的数值例子应该能让你看清楚GAT到底是怎么运作的。
GAT的核心思想
GAT的设计目标很直接:让每个节点能够智能地选择从哪些邻居那里获取信息,以及获取多少信息。
任何图都包含三个基本要素:节点(V)代表图中的实体,边(E)表示实体间的关系,特征(X)是每个节点的属性向量。
GAT层的工作流程可以概括为:输入节点特征,通过线性变换投影到新的特征空间,计算节点间的注意力分数,用softmax进行归一化,最后按注意力权重聚合邻居信息得到新的节点表示。
我们用一个简单的4节点图来演示这个过程。节点A、B、C、D的连接关系如下图所示:
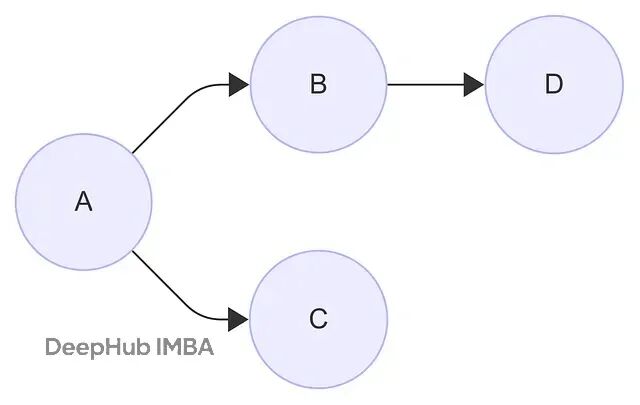
为了便于手工计算,我们设定每个节点的特征维度为3:
- 节点A:[1.0, 0.5, 0.2]
- 节点B:[0.9, 0.1, 0.3]
- 节点C:[0.4, 0.7, 0.8]
- 节点D:[0.2, 0.3, 0.9]
把这些特征向量按行排列,就得到了特征矩阵 X ∈ ℝ⁴ˣ³:

矩阵的每一行对应一个节点,每一列对应一个特征维度。我们有4个节点,每个节点3个特征,所以是4×3的矩阵。
线性变换:特征投影
GAT计算注意力之前,需要先对节点特征进行线性变换。这一步用共享的权重矩阵W将原始特征投影到新的特征空间。
线性变换的作用有两个:一是让模型能学到更好的特征表示,二是可以调整特征维度来适应不同任务的需要。数学表达式是:
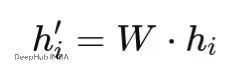

我们设定原始特征维度F=3,变换后的维度F′=2,权重矩阵W的值为(实际应用中这些权重是随机初始化然后训练得到的):

以节点A为例,它的原始特征向量是:
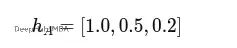
与权重矩阵W相乘得到:
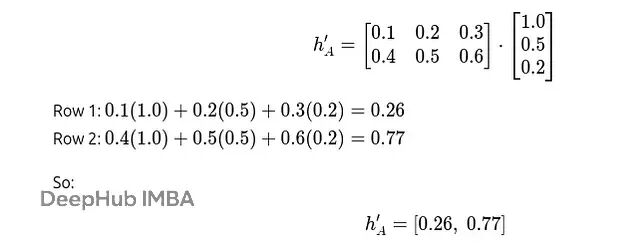
对所有节点进行同样的变换:
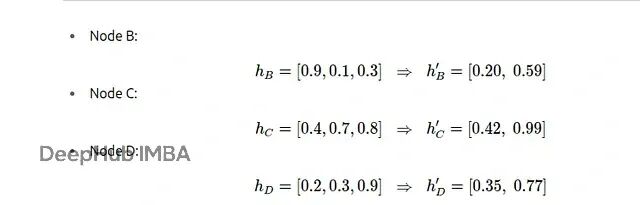
变换后的特征矩阵是:
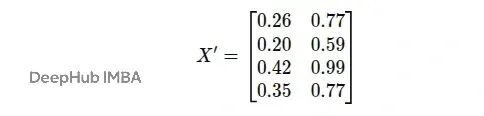
现在每个节点都从3维特征变成了2维特征。
注意力分数计算
有了变换后的特征,接下来要计算注意力分数。这些分数反映了在信息聚合时,一个节点对另一个节点的重要程度。
对于边(i,j),注意力分数的计算公式是:
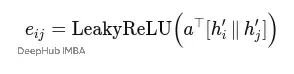

这里eij可以理解为邻居j对节点i的"原始重要性分数"。
设定变换后的特征维度F′=2,注意力向量a为(实际中这个向量也是训练学习得到的):
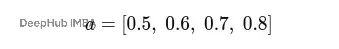
使用前面得到的变换特征:
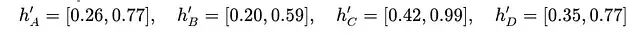
计算边A→B的注意力分数。首先将节点A和B的特征连接起来:
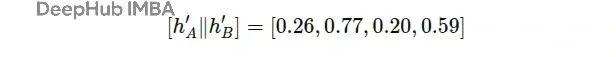
然后与注意力向量a做点积:
0.5(0.26) + 0.6(0.77) + 0.7(0.20) + 0.8(0.59) = 1.204
应用LeakyReLU激活函数(由于结果是正数,值保持不变):
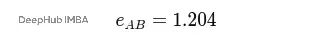
用同样的方法计算其他边的注意力分数:
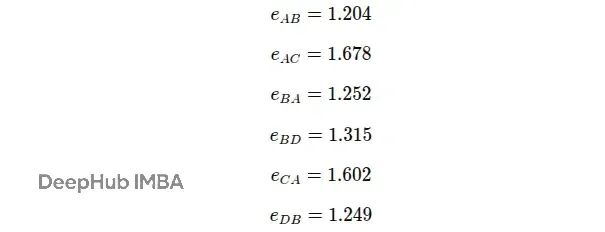
到这里得到的是未归一化的注意力分数,它们可以是任意实数。下一步需要用softmax对这些分数进行归一化,让它们变成类似概率的形式,便于比较和使用。
Softmax归一化:注意力权重分配
现在有了每条边的未归一化注意力分数eij,但这些原始分数的数值范围不一致,没法直接比较。一个节点的分数可能在1.0左右,另一个节点的分数可能在5.0左右。
Softmax函数能够解决这个问题,它将每个节点的所有邻居注意力分数转换为概率分布:
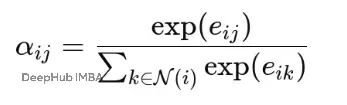
其中:
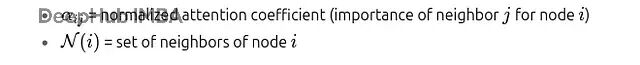
Softmax确保每个节点对其所有邻居的注意力系数加起来等于1。
以节点A为例进行计算:

结果显示节点A给B分配38.3%的注意力,给C分配61.6%的注意力。
所有节点的归一化注意力系数如下表:
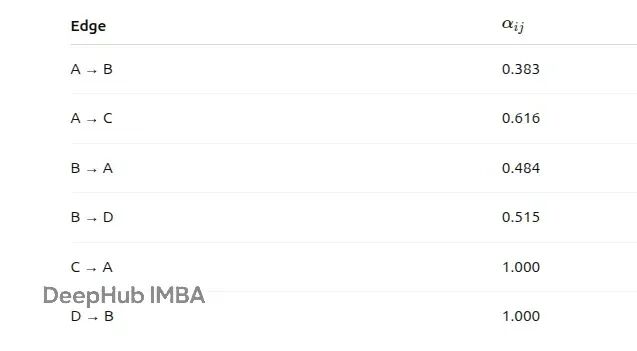
从这些结果可以看出:节点A更偏向于关注节点C而不是B;节点B在A和D之间的注意力分配比较均匀;节点C和D各自只有一个邻居,所以所有注意力都分配给了那个邻居。
特征聚合:生成新的节点表示
有了注意力系数αij,每个节点就可以通过聚合邻居的特征来更新自己的表示了:
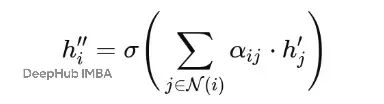

简单说就是:用重要性权重对每个邻居的特征进行加权,求和后再应用激活函数。
节点A的聚合计算过程:

所有节点聚合后的特征:
- 节点A:[0.335, 0.836]
- 节点B:[0.306, 0.769]
- 节点C:[0.260, 0.770]
- 节点D:[0.200, 0.590]
激活函数σ通常使用ELU(Exponential Linear Unit)。对于正数ELU直接保持原值;对于负数ELU会进行平滑处理而不是像ReLU那样直接置零,这种设计让模型能够学习到比线性组合更复杂的模式。
注意力机制决定了邻居的重要性,聚合过程则产生了融合邻居信息的新节点表示。
多头注意力:多视角信息融合
前面介绍的是单个注意力头的工作方式:变换特征→计算注意力→softmax归一化→聚合邻居信息。
实际应用中,GAT会同时使用多个注意力头,这个设计借鉴了Transformer架构。
多头机制的好处很明显。单个注意力头可能会过度偏向某个邻居(比如节点A对C的偏好过强),多个头可以提供不同的视角来平衡这种偏向。每个头都有自己的权重矩阵Wk和注意力向量ak,它们关注邻域的不同方面。在中间层不同头的输出通常会被拼接起来;在最终层则通常取平均值来产生最终预测。
对于K个注意力头,节点i的更新表示为:
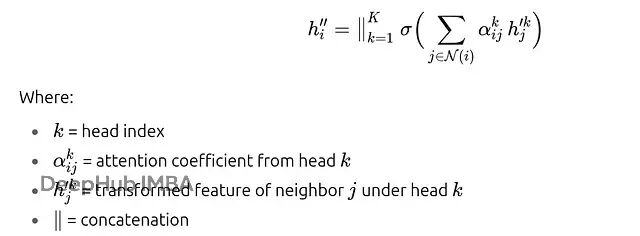
假设我们用2个头处理4节点图。头1可能学会让节点A给C分配70%权重,给B分配30%权重;头2可能学会相反的分配策略,给C分配40%权重,给B分配60%权重。当我们把两个头的结果拼接起来时,节点A的最终嵌入就包含了两种不同的邻居关系视角。
这种多样性让模型的表达能力更强,避免陷入单一的注意力模式。
GAT的训练过程
GAT layer本身只是前向计算的一部分,训练的目标是调整权重矩阵W^k 和注意力向量a^k,让网络在具体任务(比如节点分类)上表现更好。这些参数一开始是随机初始化的,然后通过反向传播不断优化。
训练流程比较标准:输入包括图G=(V,E)、节点特征矩阵X ∈ ℝ^{N×F},以及部分节点的标签。前向传播让特征通过各个GAT层,每层都进行特征变换、注意力计算和邻居聚合,最终层用softmax输出每个节点的类别概率。
损失计算通常用交叉熵,但只针对有标签的节点。反向传播计算损失对参数的梯度,这些梯度会流经注意力机制,更新邻居权重的分配策略。
优化器一般选Adam,学习率设在0.001到0.01之间。为了防止过拟合,会在节点特征和注意力系数上应用dropout,同时对权重W加上L2正则化。
多头训练让每个注意力头学习各自的参数,专注于邻域的不同特性。根据任务需要,头的输出要么拼接(捕获多个视角),要么取平均(稳定预测)。
总结
GAT的整个工作流程可以用一句话概括:线性变换→注意力计算→softmax归一化→特征聚合=上下文感知的节点嵌入。
这套机制自动解决了很多实际问题。在社交网络中谁对你影响更大,最好的朋友还是普通熟人?在分子结构中哪些原子主导了化合物的性质?在论文引用网络中经典研究和普通引用的权重应该如何分配?GAT通过学习关系的相对重要性来回答这些问题。
当然GAT也有局限性。在超大规模图上,注意力计算的开销比较高;在小数据集上,模型容易过拟合。但它已经成为图学习领域最受欢迎的工具之一,广泛应用于社交媒体分析、推荐系统、药物发现等领域。
如果你理解了GAT的数学原理和计算过程,就可以考虑在自己的领域里尝试这个方法。不管是社交网络、知识图谱还是分子生物学,GAT都有很大的应用潜力。
https://avoid.overfit.cn/post/b1c7efd4b1004512a98ebf3fcecce8e7
作者:Adarsha Pandey
