当前位置：首页 > news >正文

【论文阅读】解耦大脑与计算机视觉模型趋同的因素

news 2025/9/8 7:00:01

文章链接：https://arxiv.org/pdf/2508.18226

AI 的发展能帮助我们了解大脑吗？为什么大模型「看世界」越来越像人脑？——来自 Meta AI 的新研究。
这项研究告诉我们：

模型变大、训练时间变长、数据更贴近人类经验 → 更像人脑。
模型学会「看世界」的顺序，和人类从婴儿到成人的成长历程惊人相似。
AI 和人脑不是互相模仿，而是在相似的环境和目标下，自然收敛到了一种类似的「看图方式」。

解耦大脑与计算机视觉模型趋同的因素

Joséphine Raugel, Marc Szafraniec, Huy V. Vo, Camille Couprie, Patrick Labatut, Piotr Bojanowski, Valentin Wyart, Jean- Rémi King¹

Meta AI, ²Ecole Normale Supérieure - PSL 大学

许多在自然图像上训练的AI模型发展出了与人类大脑相似的表征。然而，驱动这种大脑- 模型相似性的确切因素仍然知之甚少。为了解耦模型架构、训练方法和数据类型如何独立地引导神经网络发展出大脑样表征，我们训练了一系列自监督视觉Transformer（DINOV3），系统地改变了这些不同因素。我们将它们的自然图像表征与使用超高频功能磁共振成像（fMRI）和脑磁图（MEG）记录的人类大脑表征进行比较，在空间和时间分析中提供高分辨率。我们使用三个互补指标评估大脑- 模型相似性，重点关注整体表征相似性、拓扑组织和时间动态。我们发现所有三个因素——模型大小、训练量以及图像类型——都独立地且交互地影响这些大脑相似性指标。特别是，使用最大量以人为中心的图像训练的最大DINOV3模型达到了最高的脑相似性分数。重要的是，AI模型中大脑样表征的出现遵循着训练过程中的特定时间顺序：模型首先与感觉皮层的早期表征对齐，并且只有在获得大量训练数据后才会与大脑的晚期和前额叶表征对齐。最后，这种发展轨迹由人类皮层的结构和功能特性所索引：模型最后获得的表征与发育扩展最大、最厚、髓鞘化最少、时间尺度最慢的皮层区域特别对齐。总体而言，这些发现解耦了架构和经验在塑造人工神经网络如何像人类一样感知世界之间的相互作用，从而提供了一个有前景的框架来理解人类大脑如何表征其视觉世界。

对应：{josephiner,jeanremi}@meta.com Meta

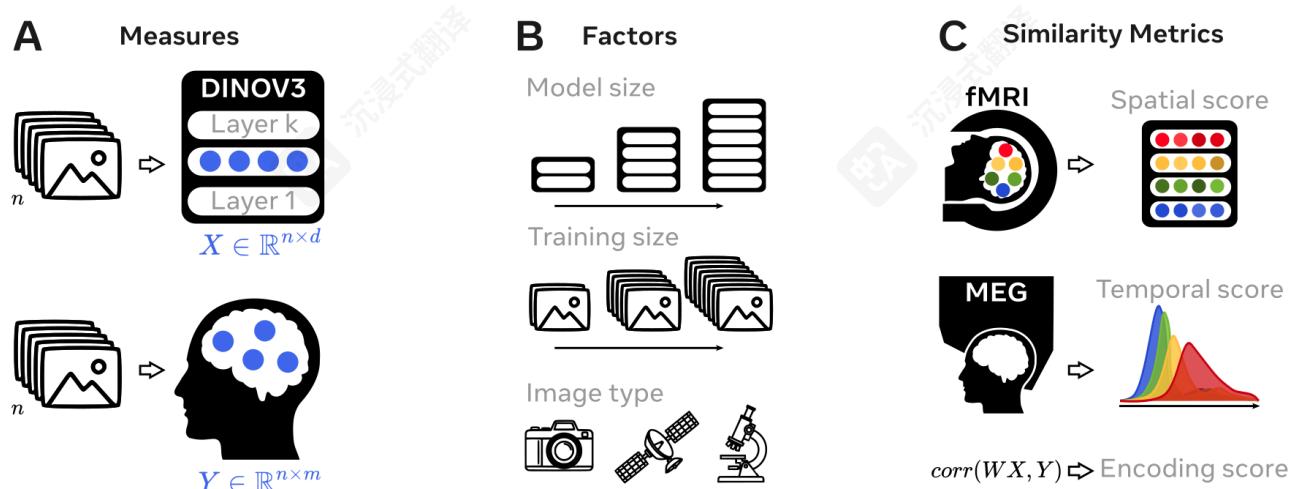
A.我们将一种在自然图像上训练的最先进的自监督计算机视觉模型DINOV3的激活与人类大脑对相同图像的响应进行比较。B.为了了解使DINOV3与大脑相似或不太相似的因素，我们在不同的图像域（人类中心相机图片、卫星图像或生物数据）上，以及使用不同数量的数据，训练了各种模型。从scratchC.我们通过计算它们表示的整体线性相似性（编码分数）以及它们层次组织的相似性（空间和时序分数），将每个模型与功能性磁共振成像（fMRI，具有高空间分辨率）和脑磁图（MEG，具有高时序分辨率）进行比较。1

1引言

1 引言脑- 人工智能相似性。深度学习在过去十年中彻底改变了计算机视觉。最先进的深度网络现在在各种任务上实现了人类水平或更优越的性能，包括分类（Siméoni 等人。,2025;Tschannen 等人。，2025），目标检测（Redmon 等人。，2016），语义分割（Cheng 等人。，2022），以及医学图像分析（Esteva 等人。，2017；Lorenci 等人。，2025）。令人惊讶的是，这些深度学习模型的内部表示似乎与人类大脑的表示相关：多种电生理学（Yamins 等人，2014a；Yamins 和 DiCarlo，2016；Schrimpf 等人，2018；Zhuang 等人，2021），功能性磁共振成像（Eickenberg 等人，2017；Millet 等人，2023；Doerig 等人，2025；Tang 等人，2023；Niko- 1aus 等人，2024），脑磁图研究（Cichy 等人，2016；Seeliger 等人，2018；Caucheteux 和 King，2022；Banville 等人，2025）现在已一致表明，这些模型的激活模式在响应相同图像时线性地映射到皮层上。

理论重要性。理解AI模型与人类大脑之间这种表示相似性的起源原理具有首要重要性，以理解可能在神经网络中普遍共享的信息处理定律。实际上，几条研究线（Hasson 等人，2020；Huh 等人,2024；van Rossem 和 Saxe,2024；Cagnetta等人，2024;Mehrer 等人,2020；Mah- ner 等人，2025；Simkova 等人，2025）表明，存在制约神经网络中表征结构和涌现的普遍原理。

挑战：原因不明确。然而，计算机视觉模型与人类之间代表相似性的精确因素目前仍不明确。这种知识差距部分是由于先前研究主要关注预训练网络，这些网络在训练目标、架构和数据机制（Conwell 等人，2021;Rajesh 等人,2024）方面同时存在差异。这些因素如何独立地以及相互作用地导致模型收敛到类似大脑的表征，目前仍不明确。

为解决此问题，我们系统地训练了多种DINOv3模型（Siméoni 等人。，2025），同时独立地改变它们的大小、数据类型和训练数量。DINOv3的优点是自监督，因此可以在不同的

类型的自然主义但非人类中心和非标记数据上，例如卫星图像（Siméoni 等人。，2025)和生物图像（Lorenci 等人。，2025）。

在这里，我们将各种DINOv3模型与通过超高频（7T）功能性磁共振成像和脑磁图（MEG）记录的大脑对图像的反应进行比较，以分别获得皮质表征的高空间和时间分辨率。为此，我们实现了三种相似性度量。首先，我们使用一种标准的线性映射度量，通常称为编码分数（Naselaris 等人，2011)，它评估两个系统表征之间的线性对应关系。其次，我们使用fMRI评估这种线性映射是否遵循类似的空间组织，其中模型的第一个和最后一个层将分别与感觉视觉皮层和前额叶皮层最佳匹配。最后，我们使用MEG评估这种映射是否遵循类似的时间组织，其中模型的第一个和最后一个层将分别与早期和晚期MEG反应最佳匹配。

2方法

2.1方法

2 方法我们旨在识别使现代计算机视觉模型处理和表示自然图像类似于人脑的因素。基于先前工作（Kriegeskorte 等人,2008；DiCarlo 等人，2012;King 和 Dehaene，2014)，我们依赖于“表征”的定义为“线性可读信息”。我们采用Naselaris等人(2011)提出的编码分析程序来评估人工智能模型与脑记录之间的表征相似性。该线性模型试图寻找是否存在一个线性映射 $W∈Rm×dW\in \mathbb{R}^{m\times d}$ 可以可靠地预测 $m$ 维度的脑活动 $(Y∈Rn×m)(Y\in \mathbb{R}^{n\times m})$ ，给定 $d$ 维度的模型激活 $(X∈Rn×d)(X\in \mathbb{R}^{n\times d})$ ，该激活是在 $n$ 图像刺激下产生的：

$\underset {W}{\arg \min}\left\{\| Y - XW\| _2^2 +\lambda \| W\| _2^2\right\}$

使用 $λ\lambda$ 作为岭正则化参数。

对于这一点，我们使用scikit- learn的RidgeCV(Pedregosa等人。，2011)并在 $λ\lambda$ 之间 $10^{0}$ 和 $10^{8}$ 之间使用5折交叉验证。

2.2指标

编码分数给定两个表示 $X$ 和 $Y$ ，我们通过分别计算每个拆分并然后取平均值，来量化它们的整体表示相似性，使用皮尔逊相关分数 $R∈[−1,1]R\in [- 1,1]$ 计算编码分数：

$R^{(d)} = corr(WX_{test},y_{test}^{(d)})$

为了清晰起见，我们可以总结跨脑维度的平均R分数，或者将它们分别绘制出来，以获取有关大脑活动是否可以从模型中线性预测的信息。在一些分析中，我们使用 $R~=R/max⁡(R)\tilde{R} = R / \max (R)$ ，即归一化编码分数，它在1处达到峰值。

空间分数为了评估模型是否像具有空间分数的大脑那样组织其处理层次结构，我们按四个步骤进行。首先，我们评估每个脑维度的编码分数 $d$ ，以及模型中的22层 $k∈[0,1]k\in [0,1]$ ，其中0是第一层，1是最后一层。其次，我们识别最佳预测这种脑反应的层： $k^{*}$ 。第三，我们近似每个脑区的层次位置 $d^{*}$ ，作为其在标准化MNI空间中与V1的欧几里得距离，单位为毫米。请注意，这是一种粗略的近似，因为实际皮质层次结构并不严格遵循这种距离，并且可能要复杂得多（Felleman andVanEssen,1991）。最后，我们将空间分数计算为 $d^{*}$ 和 $k^{*}$ 之间的相关性。为了清晰起见，我们将这些分析限制在感兴趣的区域。

时间分数为了评估来自MEG记录的类似指标，我们估计一个时间分数：即模型层 $k$ 和 $t^*$ 之间的相关性一一模型每一层在多大程度上能最大程度预测大脑活动的时间点。为了限制噪声估计，我们对 $Rˉk≥95%\bar{R}^k\geq 95\%$ 进行平均，其中 $Rˉk\bar{R}^k$ 是模型层 $k$ 的归一化脑分数。

2.3模型

架构。DINOv3是一个在1.7亿张自然图像上训练的最先进的自监督学习视觉Transformer模型（Simeoni等人，2025）。我们从零开始训练了DINOv3模型的八个变体，以确保在架构、训练规模和数据类型方面进行全面评估。

首先，我们利用经过 $1e^{7}$ checkpoints训练的DINOv3- 7B。我们比较性地分析了DINOSmall、

Base、Large和Giant，在相同配置下对1.7B图像进行 $5e^6$ training steps训练后此外，我们还训练并比较分析了DINO大型架构的三个版本：DINO人类、DINO细胞和DINO卫星。这些模型配置相似，并在10M张图像上从零开始训练；它们仅在训练图像类型上有所不同。

2.4数据集。

图片。DINOv3- 7B和DinoHuman在相同的人类中心数据上进行了训练。该数据集是从大量的网络图片中构建的，这些图片来自公开的Instagram帖子、街景和ImageNet（Deng等人。，2009)。这些图片经过了平台级的内容审核，以防止有害内容，从而获得一个约170亿张图片的数据池。该数据池按照（Simeoni等人。,2025)中的程序进行筛选，以获得一个包含17亿张图片的大规模预训练数据集。为了比较使用不同类型图片训练的模型，我们使用三种类型的自然图片（人类中心、细胞和卫星图片）中的一种重新训练了三个不同的DINOv3大型模型，这些图片在数量上是一致的（每种类型1000万张）。人类中心图片对应于用于训练原始DINOv3模型的数据集。为了对我们的人类中心、细胞和卫星图片进行比较分析，我们从这个包含17亿张图片的数据集中随机选择了1000万张图片的子集。

细胞图像对应于ExtendedCHAMMI数据集，该数据集由荧光显微细胞图像组成，揭示了细胞结构在不同通道中的表现（例如：细胞核、线粒体、微管等）（Lorenci等人，2025).

卫星图像对应于SAT- 493M数据集的一个随机子集，该数据集由从MaxarRGB正射校正影像中随机采样的约5亿个样本组成，分辨率为0.6米（Simeoni等人，2025).

脑磁图(MEG)。我们使用THINGS- MEG数据集（Hebart等人。，2023a），该数据集包含四名健康受试者观看22,500张自然图像的MEG录制，代表总共1,800个物体概念（Hebart等人。，2023b）。图像在1.5秒内呈现，同时受试者保持注视。为了限制噪声的影响，我们在0.1到 $20Hz20\mathrm{Hz}$ 之间应用带通滤波器，以 $30Hz30\mathrm{Hz}$ 对信号进行降采样，将大脑反应与单个单词进行时间锁，并对

Table1DINOV3模型变体的规格说明

模型	参数	层	批大小	图像
DINov3	7B	40	4096	以人为本 1.7B
DINov3 Giant	1.1B	32	4096	以人为本 1.7B
DINov3 Large	300M	24	4096	以人为本 1.7B
DINov3 Base	86M	12	4096	Human centric 1.7B
DINov3 Small	21M	12	4096	Human centric 1.7B
DINov3 Human	300M	24	2048	Human centric 10M
DINov3 Cellular	300M	24	2048	Cellular 10M
DINov3 Satellite	300M	24	2048	Satellite 10M

相应的神经数据在单词出现前- 0.5秒到 $+ 3$ 秒之间相对单词出现使用MNE- Python（Gramfort等人。2013）。最后，我们对每个MEG通道和每个时间点的MEG信号进行z分数。

时间ROIs。我们研究图像处理过程中三个5秒长的时间ROIs，以研究每个层在认知过程中相对影响。这些时间窗口跨越.08- .13s、.13- .18s和.5- .55s。

$T_{max}^{layer}$ 。为了研究每一层的动态，我们计算 $TmaxlayerT_{\mathrm{max}}^{layer}$ 即时间窗口的平均值，在此期间 $R^layer≥95%\hat{R}^{layer}\geq 95\%$ ，其中 $R^layer\hat{R}^{layer}$ 是每一层的归一化脑分数。

功能磁共振成像(fMRI).我们利用了自然场景数据集(Allen等人.,2022)，一个7特斯拉fMRI数据集，其中包含来自八个受试者的记录，每个受试者在4秒内观察总共10000个自然场景，同时执行持续识别任务。我们在图像出现后的5.5秒对fsaverage表面上的BOLD信号进行编码。这个时间点对应于从BOLD信号解码图像的峰值。

感兴趣区域(ROIs)。为了清晰起见，我们选择了一组代表性的15个感兴趣区域(ROIs)，这些区域跨越了皮层解剖结构，在平均FDR校正的t检验p值 $< 0.01$ 的区域中，这些区域由形成ROIs的体素编码）。这些ROIs从后枕叶分布到前额叶皮层。为了研究索引表征相似性的皮层特性，我们根据四个皮层图谱分析我们的结果，这些图谱通过Neuromaps（Markello等人.，2022)提供：皮质扩张(Hill等人，2010)反映了婴儿和成人皮质表面积的差异。

髓鞘浓度是根据HCCPS1200数据集中的T1w/T2w比率估计的（VanEssen等人，2013）。

固有时间尺度是从电磁网络（通过MEG测量）映射到

血流动力学网络（通过fMRI测量）并对每个区域的时序积分窗口进行索引（Shafiei等人，2021）。

皮质厚度是通过测量人类连接组计划（Fischl,2012）结构MRI中"白质"和"软脑膜"表面之间的距离来估计的（VanEssen等人，2013）。

2.5统计学

fMRI体素。我们仅绘制和分析在FDR校正的t检验后 $p<0.01\mathrm{p}< 0.01$ 阈值化的体素。跨受试者。为了评估跨受试者的统计估计，我们使用scipy（Virtanen等人，2020）执行Wilcoxon检验。为了校正多重比较，我们应用了MNE- Python（Gramfort等人，2013）中实现的假发现率校正。

半次。为了分析DINO模型在训练过程中的收敛速度，我们估计了“半次’：相似度指标达到其最终值一半的相对训练步数。

3结果

3.1DINOV3-大脑相似度

编码分数。为了验证DINOV3生成的自然图像表示是否与大脑的相似，我们通过评估DINOV3和大脑对相同图像的激活之间的线性映射，进行交叉验证的编码分析。功能磁共振成像结果显示，DINOV3的表示主要在视觉通路（ $R=.45±.039\mathrm{R} = .45\pm .039$ - 受试者间SEM），主要在外侧枕瓣叶（MT: $R=.34±.026)\mathrm{R} = .34\pm .026)$ 和腹内侧视觉皮层（VMV2: $R=.28±.025)\mathrm{R} = .28\pm .025)$ ，图2A。

MEG结果显示，这种相似性在图像呈现后约70毫秒时上升 $(R=.09±.017\mathrm{(R = .09\pm .017}$ ，图2B)并重新

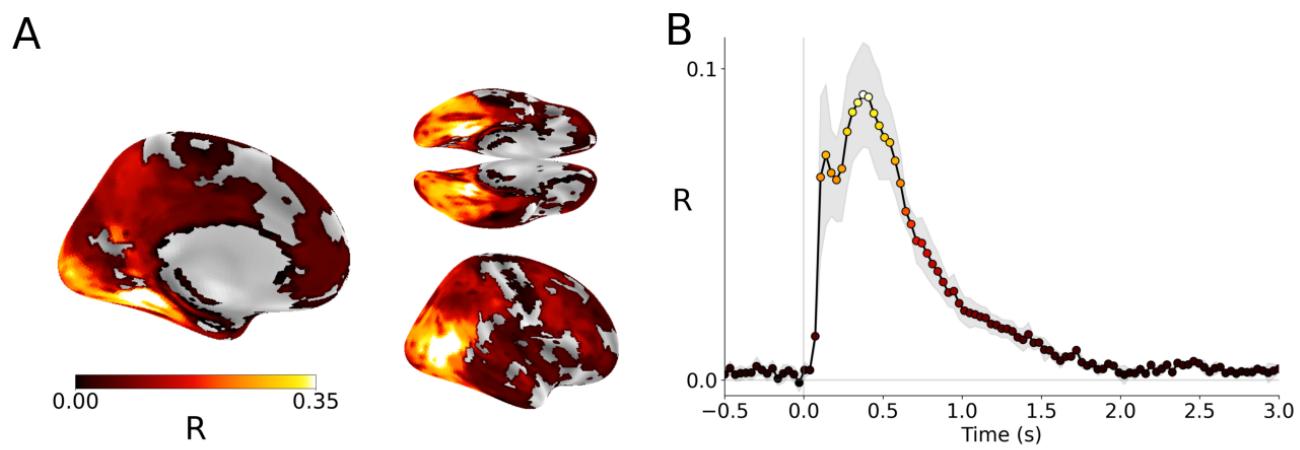
图2 大脑-DINOV3相似性。A. DINOv3嵌入与对应图像的fMRI响应之间的相似性，使用Pearson大脑分数估计，并在 $p<0.01\mathrm{p}< 0.01$ 上fdr校正阈值化（左侧：左半球的内侧视图，右上：底部视图；右下：右半球的侧视图）。B. DINOv3嵌入与对应图像的MEG响应之间的相似性。误差线表示在观看静态图像的4名受试者之间平均值的标准误差。

显著高于随机水平，直到图像呈现后3秒 $(p<1e−4)(\mathrm{p}< 1\mathrm{e}^{- 4})$ 。

这些结果与过去的研究（Eickenberg等人，2017；Schrimpf等人，2018；Tang等人，2025）一致，并且额外表明通常从视觉通路中丢弃的区域，例如前额叶区域BA44、BA45、IFSa和IFSp，也表现出可以线性预测自AI嵌入的激活。

空间分数。DINOv3的表示层次结构是否与人类大脑的视觉层次结构相对应？为了回答这个问题，我们估计了“空间分数”。fMRI结果证实，DINOv3的最低层倾向于最好预测低级感觉区域（如V1），而最高层则倾向于最好预测大脑的高级区域（如前额叶皮层（图3A、C、E）。大脑每个区域与V1之间的欧几里得距离（i）与最佳编码层（ii）之间的皮尔逊相关性高度显著， $R=0\mathrm{R} = 0$ 。38， $p<1e−6\mathrm{p}< 1e^{- 6}$ （图3E）。

时间分数。为了补充这个fMRI"空间分数"，我们评估了一个MEG"时间分数"。为此，我们识别了在MEG中相对于图像开始时间预测每个时间ROI的最佳层（图3B）。结果表明， $TmaxlayerT_{\mathrm{max}}^{layer}$ 与层之间存在显著相关性，此处称为时间分数（图3B，D，F）。时间分数 $R=0.96\mathrm{R} = 0.96$ $p<1e−12\mathrm{p}< 1e^{- 12}$ ，表明DINOv3的第一层和最后一层分别与最早和

最新的MEG响应一致。

3.2 什么因素导致DINOv3变得像大脑？

训练的影响。为了阐明DINOv3中大脑样过程的涌现，我们评估了DINOv3每个选定训练步骤的编码分数、空间分数和时间分数，然后使用“半时间”总结它们的发展速度：即达到最终分数一半的训练步骤。

首先，在编码分数达到 $R=.03±2e−4\mathrm{R} = .03\pm 2e^{- 4}$ 之前训练，之后训练最终收敛到 $R=.09±5e−4\mathrm{R} = .09\pm 5e^{- 4}$ 。这些R分数在体素上平均——最佳体素在 $R=.45±.038\mathrm{R} = .45\pm .038$ （图4A，B，E）。编码分数的半衰期发生在训练的 $2%2\%$ 左右，大约是 $10^{5}$ 训练步数（即80亿张图像）。其次，时间分数比脑分数出现得更快：半衰期约为训练的 $0.7%0.7\%$ ，并在 $R=0.96\mathrm{R} = 0.96$ $(p<1e−12)(\mathrm{p}< 1e^{- 12})$ 收敛。最后，空间分数在训练的 $4%4\%$ 时达到半衰期，并收敛到 $R=0\mathrm{R} = 0$ 。4 $(p<1e−6)(\mathrm{p}< 1e^{- 6})$ 。这些发育轨迹在感兴趣的时间和脑区中是否相同？为了解决这个问题，我们在感兴趣的具体区域或时间窗口上评估相同的分析。功能磁共振成像结果表明，低级视觉区域（例如V1、V2）的半衰期低于高级前额叶皮层（例如IFSp、IFSa；图5A,C）。半衰期与解剖位置（粗略定义为到V1的欧几里得距离）之间的相关性为 $R=0\mathrm{R} = 0$ 。91， $p<1e−5\mathrm{p}< 1e^{- 5}$ 。Sim-

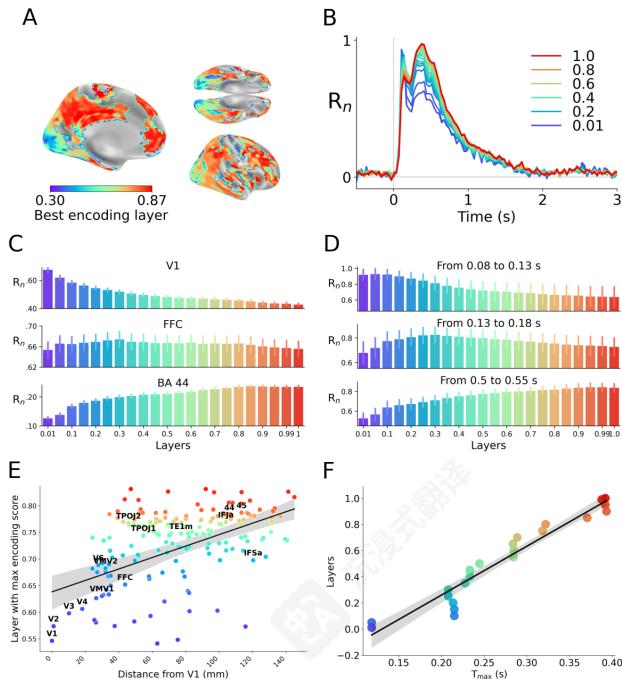
图3 DINOv3的表征层次结构与大脑的A. 体素最佳编码层（DINOv3），经FDR校正并阈值化于 $p<0.01\mathrm{p}< 0.01$ （左：左侧大脑半球内侧视图，右上：底部视图；右下：右侧大脑半球外侧视图）。B.DINOv3每一层与对应静息图像的MEG响应之间的动态脑分数随时间变化。C. 皮质三个感兴趣区域（V1（上）、梭状回（中）和Broadmann 44（下））的层间缩放脑分数。编码分数按每层的最大编码分数缩放，该分数是15个研究ROI中该层的最大编码分数。D. 图像处理过程中三个时间窗口（.08- .12s（上），.13- .18s（中）和5. - .55s（下））的层间缩放脑分数。编码分数按每层的最大时间编码分数缩放。E. 绘制每个区域最佳编码层与该区域到V1的欧几里得距离（毫米）之间的相关性。Pearson相关系数为 $r=0.38\mathrm{r} = 0.38$ ， $p<1e−6\mathrm{p}< 1\mathrm{e} - 6$ 。绘制区域经FDR校正并阈值化于 $p<0.01\mathrm{p}< 0.01$ 。F. 绘制每个时间步最佳编码层与 $TmaxlayerT_{\mathrm{max}}^{\mathrm{layer}}$ （秒）之间的相关性。Pearson相关系数为 $r=0.84\mathrm{r} = 0.84$ ， $p<1e−5\mathrm{p}< 1\mathrm{e} - 5$ 。绘制区域经FDR校正并阈值化于 $p<0.01\mathrm{p}< 0.01$ 。

类似地，对于MEG，早期窗口（例如 $200\mathrm{ms}$ ）的半衰期低于晚期时间窗口（例如 $>1,500ms>1,500\mathrm{ms}$ ；图5B,D）。半衰期与时间峰值之间的相关性为 $R=0\mathrm{R} = 0$ 。84, $p<1e−5\mathrm{p}< 1e^{- 5}$ 。总的来说，这些结果表明，感觉和前额叶皮层的脑反应包含了在DINOv3的训练中相对较早和较晚获得的图像的表示。

模型大小的影响。更大规模的Dino模型似乎收敛更快，并且更准确地编码高级别的ROI。模型大小如何影响收敛？模型大小始终导致训练结束时更大的编码分数（ $RGiant=R_{\mathrm{Giant}} =$ $R_{\mathrm{Large}} = 0.105 > R_{\mathrm{Base}} = 0.101 > R_{\mathrm{Small}} = 0_{\circ}$ 096与 $p<1e−3\mathrm{p}< 1e^{- 3}$ )，图6B)。类似地，空间分数和时序分数也存在类似的、但更嘈杂的现象 $(p<1e−3)(\mathrm{p}< 1e^{- 3})$ ，图6A，B。

模型大小是否以类似的方式影响不同ROI的编码分数？对每个ROI分别应用相同的分析（图6C，D）表明，与视觉皮层（如V1，V2）相比，模型大小主要增加高级别皮层（如BA44和IFS）的编码。所有模型在高级别ROI中显著表现出这种与大小相关的编码增加，只有最小的模型在V1，V2 $(p<1e−3)(\mathrm{p}< 1e^{- 3})$ ，图6C，D。

图像类型的影响。为了评估图像类型如何影响模型中类脑表征的发展，我们从零开始训练了三个不同的DINO模型，每个模型使用一个自然图像数据集：卫星图像、细胞图像和经典（以人为中心）图像。我们专注于单个DINOv3架构（Dino Large），具有固定的训练长度和训练数据量（10M图像），并将数据类型作为唯一变化的因素。训练提高了所有图像类型的编码分数、空间分数和时间分数（图7A），表明这些模型学习了跨这些不同类型自然图像的通用视觉特征。然而，对于卫星图像和细胞图像，这些类脑相似性指标在编码、空间和时间分数方面低于以人为中心的图像。有趣的是，这种差异在大多数感兴趣区域都观察到：例如，V1 $(p<1e−3)(\mathrm{p}< 1e^{- 3})$ 和 $IFSa(p<1e−3)\mathrm{IFSa(p< 1e^{- 3})}$ 都由使用以人为中心的照片训练的模型更好地编码。在训练结束时，Dino Human在脑分数、时间和空间分数方面达到了显著更高的性能 $(p<1e−3)(\mathrm{p}< 1e^{- 3})$ ，图7B。这些结果可能源于以人为中心的图像反映了大脑接触到的视觉输入，而卫星图像和细胞图像是大脑未经过训练处理的图像。

3.3 与皮质特性的关联

大脑样表征的发展是否由皮质的机能、结构和发育特性所决定？为了探讨这一问题，我们评估了编码表征半衰期与皮质四个特性之间的相关性。

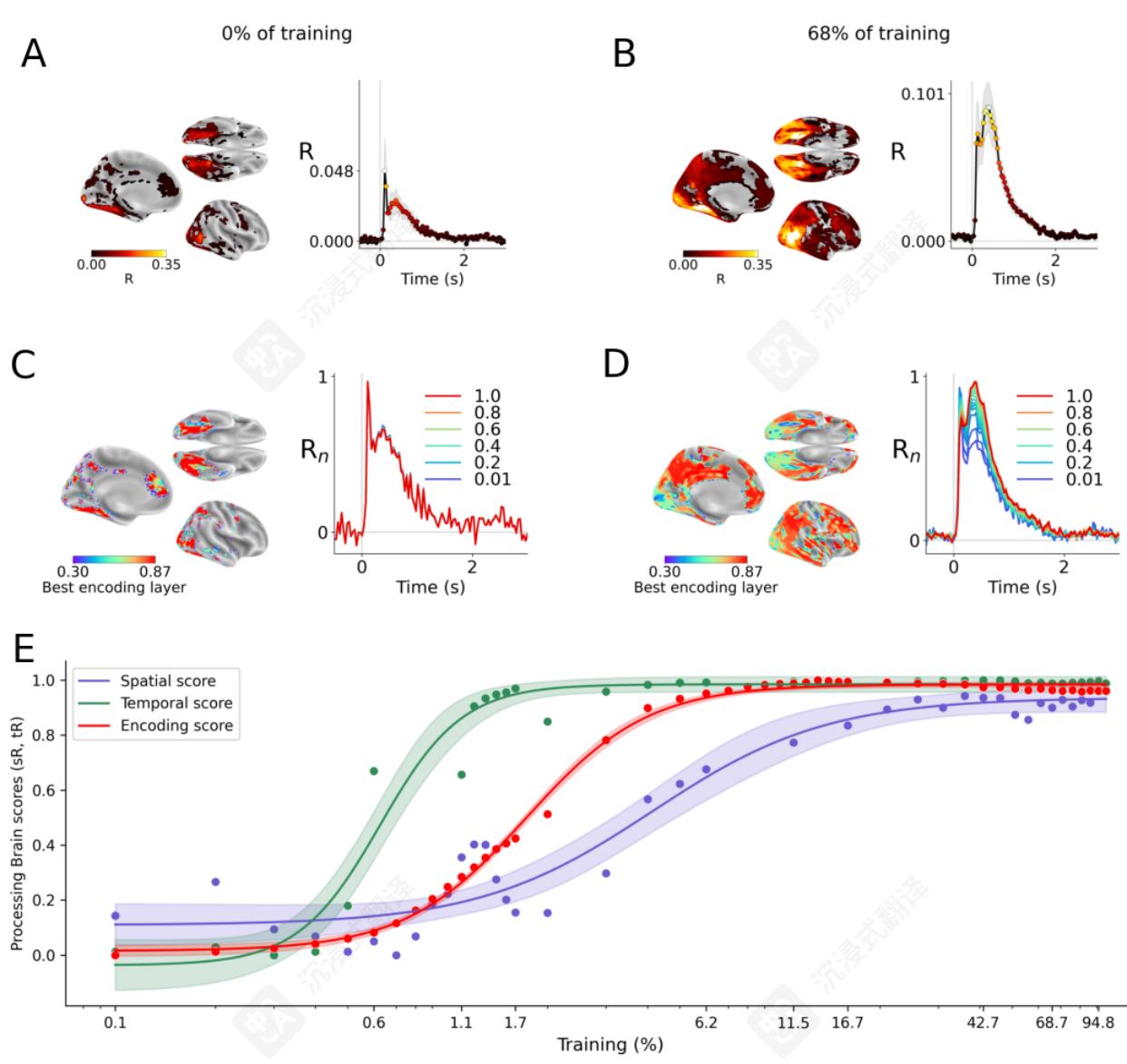
图4 A. fMRI和MEG编码分数来自一个未训练的DINOv3。B. $68%68\%$ 训练的DINOv3的编码分数。C. 未训练的DINOv3的分数。左。每个fMRI ROI的每个体素的最佳编码层。右。未训练的DINOv3的10个代表性层的相对编码分数（ $0 =$ 第一层， $1 =$ 最后一层）。D. C的相同内容，适用于 $68%68\%$ 训练的DINOv3。E. 时间、编码和空间分数随DINOv3训练变化的演变。

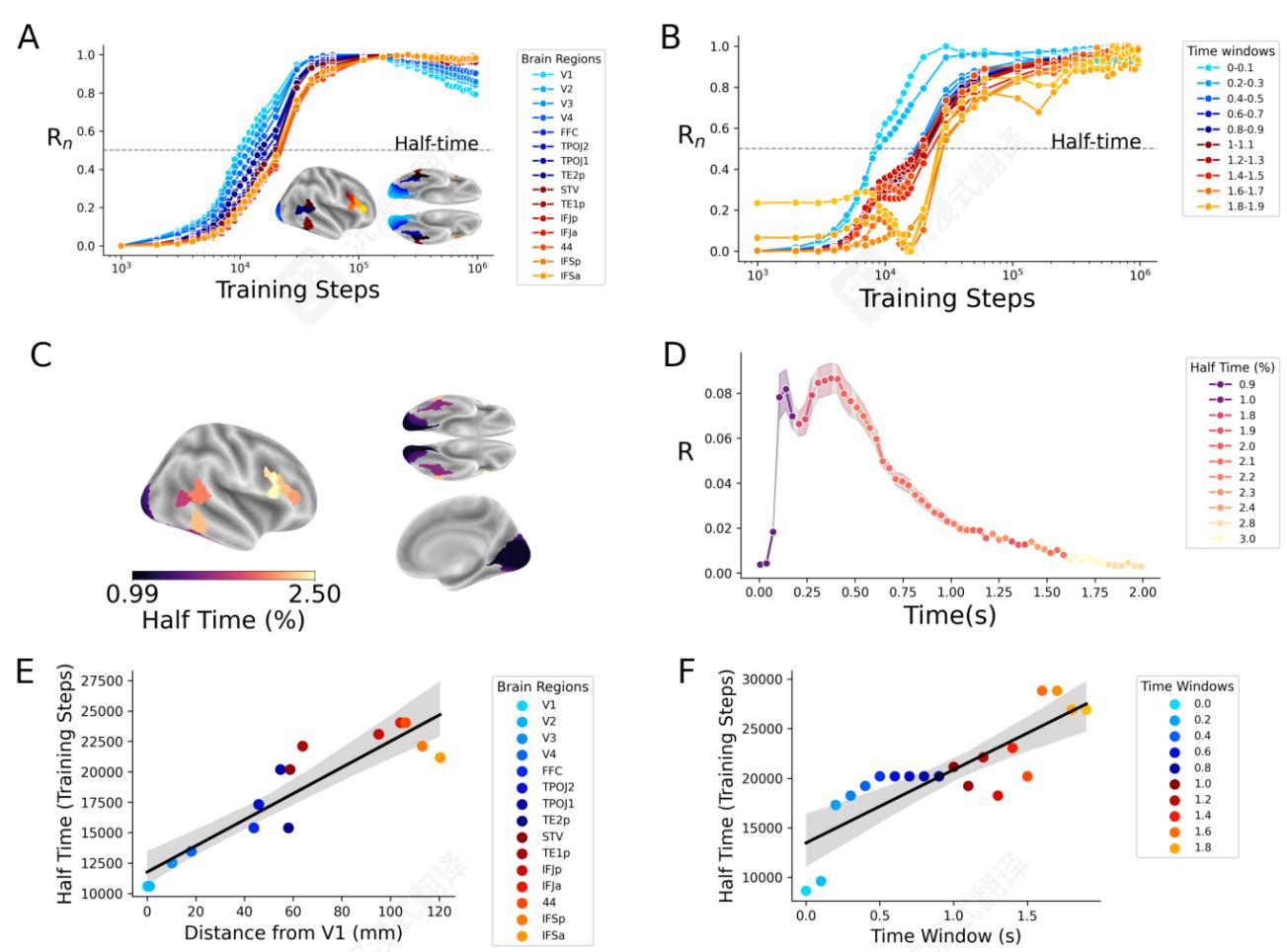
图5 脑样表征的出现。A. 每个脑ROI的归一化脑编码分数随训练的变化。虚线表示每个区域的 $50%50\%$ 最大编码分数。B. 与A相同，但为MEG时间区域感兴趣点。C. 每个脑区域感兴趣点的时间的一半。D. 每个时间区域感兴趣点的时间的一半。E. 编码分数随训练的时间的一半与每个ROI到V1的距离之间的相关性。F. 编码分数随训练的时间的一半与编码的认知过程的时间位置之间的相关性。

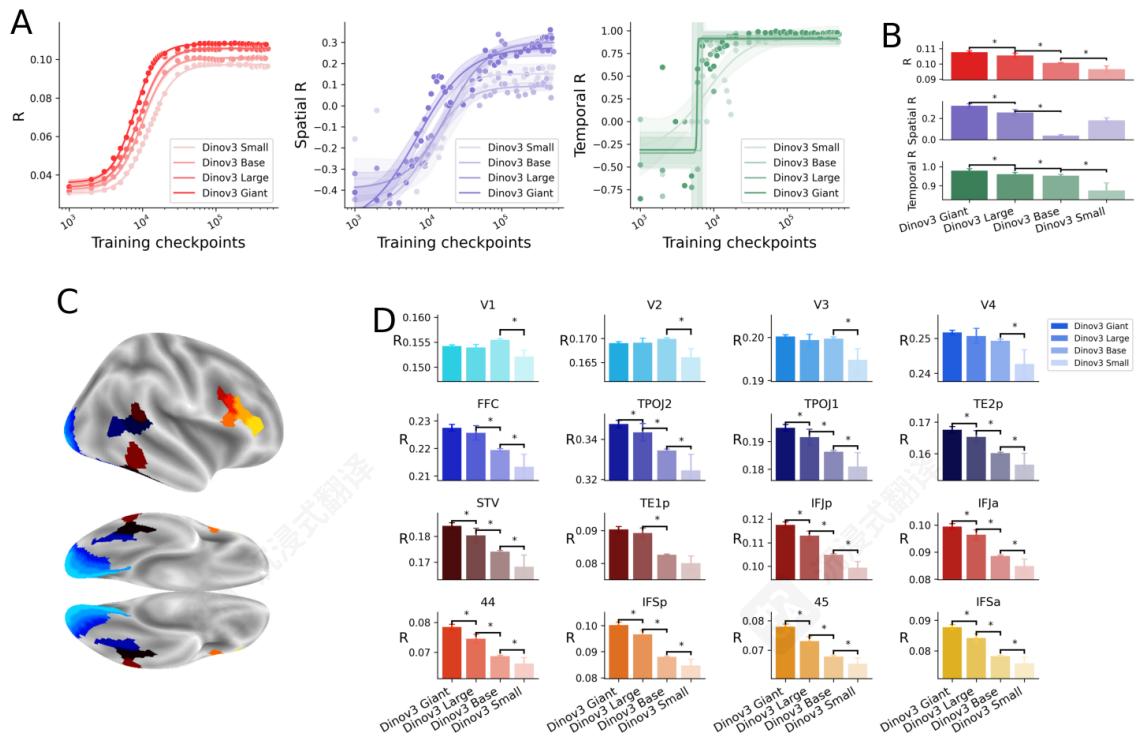
图6模型大小的影响。对于跨模型比较，显著性以 $p< 1e^{- 3}$ 表示，用星号 $∗^*$ 标注。A.编码（红色）、空间（紫色）和时间分数（绿色）随训练和模型大小的变化。训练中分数的对数拟合。B.在最终 $k = 4e^5$ 训练步骤上的分数。C.脑ROI。D.每个ROI在训练结束时的编码分数。

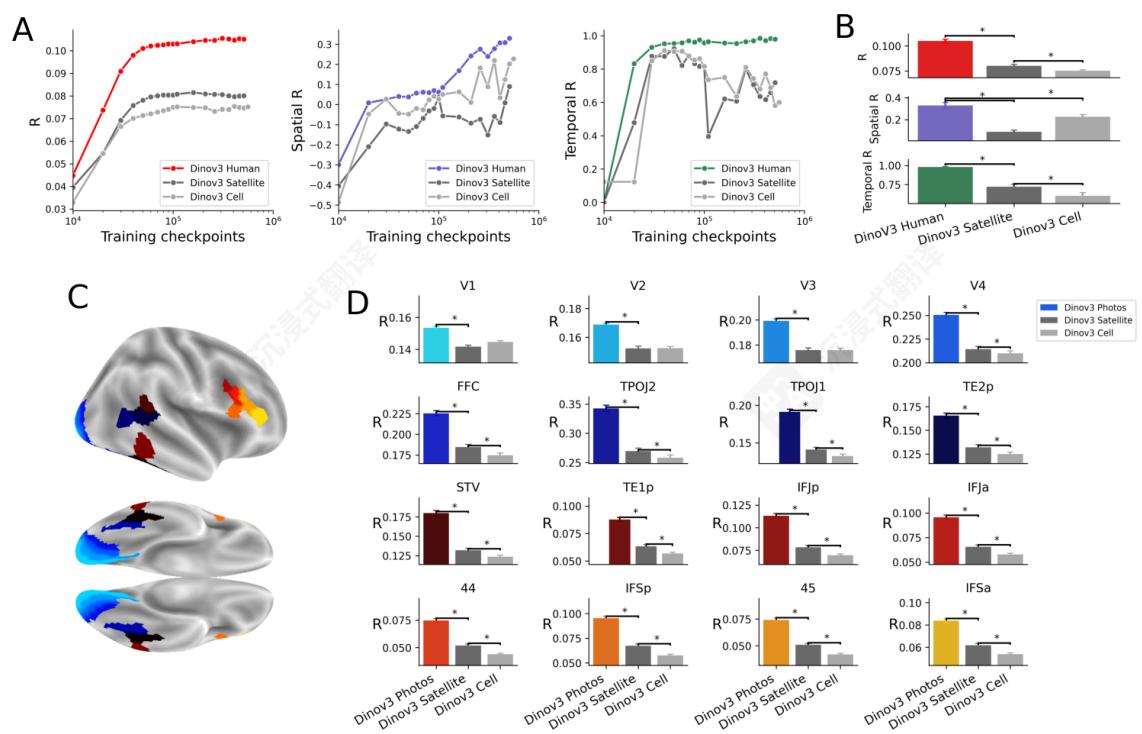
图7图像类型的影响。对于跨模型比较，显著性以 $p< 1e^{- 3}$ 表示，用星号 $∗^*$ 标注。A.编码（红色）、空间（紫色）和时间分数（绿色）随训练和图像类型的变化。B.在最终 $k = 4e^5$ 训练步骤上的分数。C.脑ROI。D.每个ROI在训练结束时的编码分数。

皮质扩张。首先，我们关注皮质区域的发育扩张。使用一个比较婴儿和成人皮质结构的图谱（Hill等人，2010），我们发现半时间与皮质扩张之间存在很强的正相关（ $R=0.88\mathrm{R} = 0.88$ ， $p<1e−3\mathrm{p}< 1e^{- 3}$ ）（图8A）。这表明皮质区域中发育增长更大的区域也是那些在AI模型中表征出现较晚的区域。

皮质厚度。其次，我们评估与皮质厚度的对应关系，利用HCPS12000估计值。我们的结果显示出显著的相关性（ $R=0.77\mathrm{R} = 0.77$ ， $p<1e−2\mathrm{p}< 1e^{- 2}$ ），表明皮质区域中皮质表面积较大的区域具有较长的半时间（图8B）。

皮质动力学。第三，从MEG活动的源重建估计的最慢内在动力学区域也是那些倾向于具有最长半时间的区域（ $R=0.71\mathrm{R} = 0.71$ ， $p=.022\mathrm{p} = .022$ ）。这一结果直接呼应了我们的MEG结果（图5），其中DINOv3的深层倾向于与较慢的大脑反应相关（图8C）。

皮质髓鞘。最后，这种动态特性似乎与髓鞘浓度（VanEssen等人，2013）相关。髓鞘，它促进了更快的神经元传输，与半衰期表现出强烈的负相关（ $R=−0.85\mathrm{R} = - 0.85$ ， $p\mathrm{p}$ - val $1e^{- 3}$ ）。这意味着较高的髓鞘浓度与较短的半衰期相关（图8D）。

总之，这些发现表明，在AI模型中脑类表征出现的速度与皮质在发展和成熟后的各种结构和功能特征之间存在强烈的预测关系。

4讨论

主要发现。理解人工神经网络为何发展出与人类大脑相似的表征，仍然是神经科学和AI（Huh等人，2024；Hasson等人，2020；Shen等人，2025；Caucheteux和King，2022）。尽管近期研究已记录到跨多种架构和训练范式的大脑- 模型相似性（Conwell等人，2022），但导致这种趋同的确切因素仍不明确。在此，我们独立操控三个独立因素——模型大小（从DINOv3小型到巨型）、训练长度（从0到 $1e^{7}$ 步，在多个包含10M和1.7B图像的训练集上进行）和图像类型（以人为中心、卫星图像和生物图像）来测试它们各自如何促成自然图像大脑样表征的出现。我们的发现表明，这三个因素都独立地且交互地影响着自监督模型趋同于大脑样视觉处理的程度。

原生论和经验论。特别是，模型- 大脑相似性随着更大的架构、更长的训练和更多生态上有效的数据而持续增加。这些结果与越来越多的研究一致，这些研究显示了自然图像的线性对齐表征（Yamins等人，2014b；Kriegeskorte，2015；Schrimpf等人，2018；Tang等人，2025；Thobani等人，2025），具有映射视觉皮质功能组织的层次结构（Eickenberg等人，2017；LaTour等人，2022），以及反映模型层排序的动态特性（Seeliger等人，2018；Cichy等人，2016；Caucheteux和King，2022）。

除此之外，我们的研究还提供了其他贡献。

首先，这种模型- 大脑对齐不仅局限于视觉通路（Eickenberg等人，2017；Schrimpf等人，2018；Tang等人，2025）而扩展到高级别——多模态——的大脑皮层区域，包括前额叶皮层（尽管例如Solomon等人（2024）在前额叶中识别出的一组低维图像特征）。

其次，我们对模型大小、训练时长和数据类型的独立操控进一步展示了这些因素如何相互作用：最大的架构与大脑活动最佳对齐，因为(1)它们被训练，以及(2)在生态相关的自然图像上。

第三，即使是非人类中心的数据集（卫星图像、生物图像）也支持早期视觉区域的局部收敛，这意味着跨环境共享的低级统计信息足以启动早期表征。总体而言，这些结果表明，虽然架构提供了潜力，但数据在使这些系统学习与大脑相似的表征方面仍然至关重要。架构、训练和数据之间的这种相互作用为认知科学中关于先天论与经验论的长期争论提供了一个经验框架，——展示了在认知发展中“先天”和“经验”如何相互作用。

走向视觉皮层发生学模型。该模型- 大脑对齐遵循一个令人惊讶的稳定发展轨迹。在训练早期，模块-

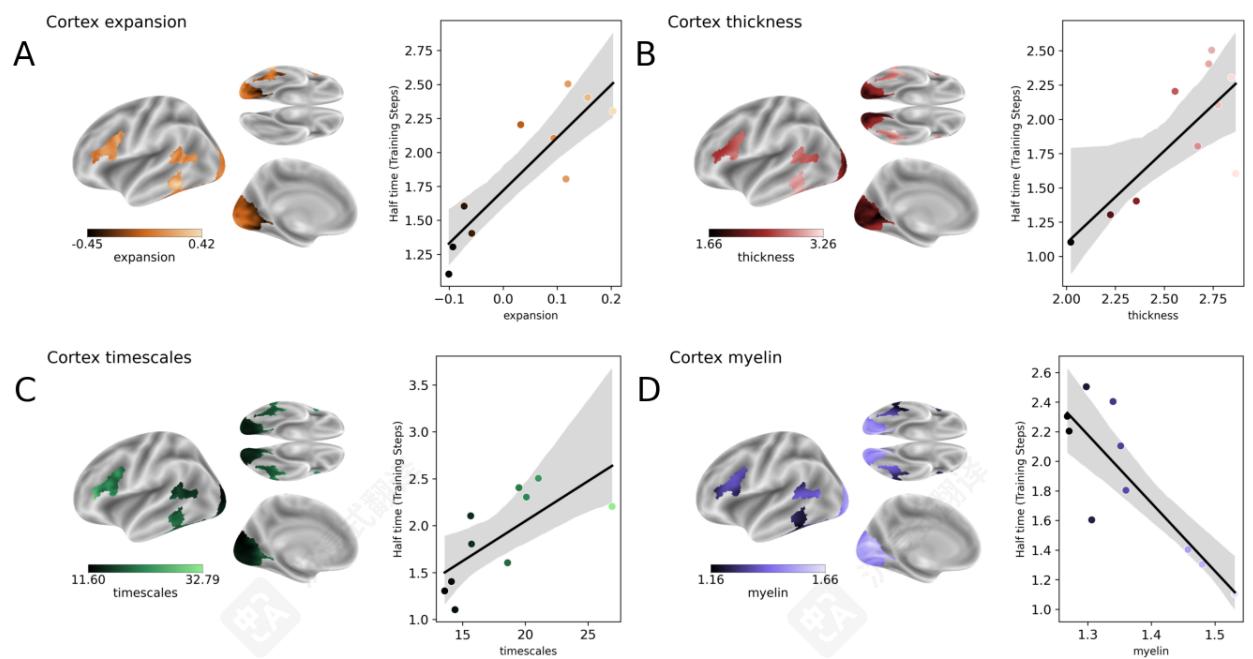
图8共享表征与皮质特性的关系。A.左。皮质扩张指数，根据成人脑和婴儿脑的差异估计，每个ROI（Hill等人，2010）。右。皮质扩张与半时间的相关性。每个点是一个ROI。B.与A相同，用于皮质厚度，根据（Van Essen等人，2013）。C.与A相同，用于皮质时间尺度，根据（Shafiei等人，2021）中的MEG源重建。D.与A相同，用于髓鞘浓度，根据（Van Essen等人，2013）。

迅速获取与感觉皮层快速、低层视觉反应相一致的表征。相比之下，慢速和高层表征的出现——特别是与前额叶皮层相一致的表征——似乎需要远超更多的训练数据。

这种发育轨迹反映了人类皮质的生命发育：AI模型在训练中最后对齐的大脑区域正是那些皮质厚度最大、内在时间尺度较慢、成熟时间延长和髓鞘化水平较低的区域——即那些在生命的头二十年缓慢发育的联合皮质区域（Dehaene，2021）。这一结果表明，人工神经网络中表征的顺序获取可能会自发地模拟大脑功能的一些发育轨迹。通过这种方式，它们最终可能提供一个新的计算框架来理解生物系统中视觉处理的阶段性成熟（Vogelsang等人，2024）。

遵循这种特定的顺序。其次，空间分数和时间分数在模型训练开始时最初为负值。这意味着随机DINOv3的最深层在训练的非常早期（但不是晚期）阶段倾向于最佳预测快速和低级的脑部反应。最后，这三个指标的一半时间是在 $1%1\%$ 和 $4%4\%$ 之间达到的——即仅 $n=1.6B\mathrm{n} = 1.6\mathrm{B}$ 张图像——的DINOv3训练数量。这表明，虽然类似脑部的低级表征非常快即可学习，但脑部的高级表征需要大量数据才能完全获取。

局限性。尽管这项研究对大脑- 模型收敛进行了受控分析，但仍有一些局限性值得考虑。首先，我们的研究结果仅基于一种自监督视觉模型系列（DINOv3），该系列在设计上是分层的。因此，尚不清楚在其他架构和训练目标下是否会出现类似的时空和编码分数（Conwell等人，2021）。其次，fMRI和MEG提供的分辨率有限，因此只能提供粗粒度的群体水平大脑活动，可能忽略精细的神经机制。第三，我们的分析仅限于成年大脑，而这些问题尚未解决这些对齐如何在发育过程中出现。

开放性问题。一些结果未被预期。首先，时间分数、编码分数和空间分数似乎不会同时出现——因此引出了一个新的问题：为什么这些指标

了解这些对应关系何时出现将需要婴儿、儿童或纵向队列的数据（Evanson等人，2025）。最后，虽然我们量化了模型和大脑之间表示的相似性，但这些神经元表示的确切性质和语义结构仍然是持续深入研究的主题（Gifford等人，2025；Graumann等人，2022）。缩小这种可解释性差距无疑仍然是神经科学和人工智能面临的重大挑战。

结论: 除了描述AI模型与大脑之间自发的收敛特性之外，这些发现还指明了利用AI模型作为工具来研究人类大脑中生物视觉组织原则的路径。通过展示机器如何能够像我们一样看见，我们的发现为人类大脑如何看见世界提供了线索。