当前位置：首页 > news >正文

五.贪心算法

news 2025/9/8 5:28:55

文章目录

- 应用场景—集合覆盖问题
- 贪心算法介绍
- 谈心算法最佳应用—集合覆盖
- - 思路分析图解
  - 代码实现
- 贪心算法注意事项和细节

应用场景—集合覆盖问题

假设存在下面需要付费的广播台，以及广播台信号可以覆盖的地区。如何选择最少的广播台(找一个最小集合的广播台)，让所有的地区都可以接收到信号

广播电台覆盖地区

K1 “北京”，“上海”，“天津”

K2 “广州”，“北京”，“深圳”

K3 “成都”，“上海”，“杭州”

K4 “上海”，“天津”

K5 “杭州”，“大连”

贪心算法介绍

1）贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法

2）贪婪算法所得到的结果不一定是最优的结果，比如说考虑到成本就不一定是最优解(有时候可能是最优解)，但是都是相对近似(接近)最优解的结果

谈心算法最佳应用—集合覆盖

1）有五个广播台，每个广播台覆盖的地区也告诉你了，现在要求你挑选最少的广播台的集合，能够覆盖所有的地区

2）为啥需要贪心算法

如何找出覆盖所有地区的广播台的集合呢？使用穷举法实现，列出每个可能的广播台的集合，这被称为幂集。假设总的有n个广播台，则广播台的组合总共有2^n-1个，假设每秒可以计算10个子集，如图

广播台数量n	子集总数2^n	需要的时间
5	32	3.2秒
10	1024	102.4秒
32	4294967296	13.6年

在进行组合的情况下，用穷举法，效率很低，因此我们需要贪心算法来解决

3）如何用贪心算法解决集合覆盖问题：

使用贪心算法效率高

目前并没有算法可以快速计算得到准确的值，使用贪心算法，则可以得到非常接近的解，并且效率高。选择策略上，因为需要覆盖全部地区的最小集合：

1）遍历所有的广播电台，找到一个覆盖了最多未覆盖地区的电台(此电台可能包含一些已覆盖的地区，但没有关系)

2）将这个电台加入到一个集合中(比如ArrayList)，想办法把该电台覆盖的地区在下次比较时去掉

3）重复第1步直到覆盖了全部的地区

思路分析图解

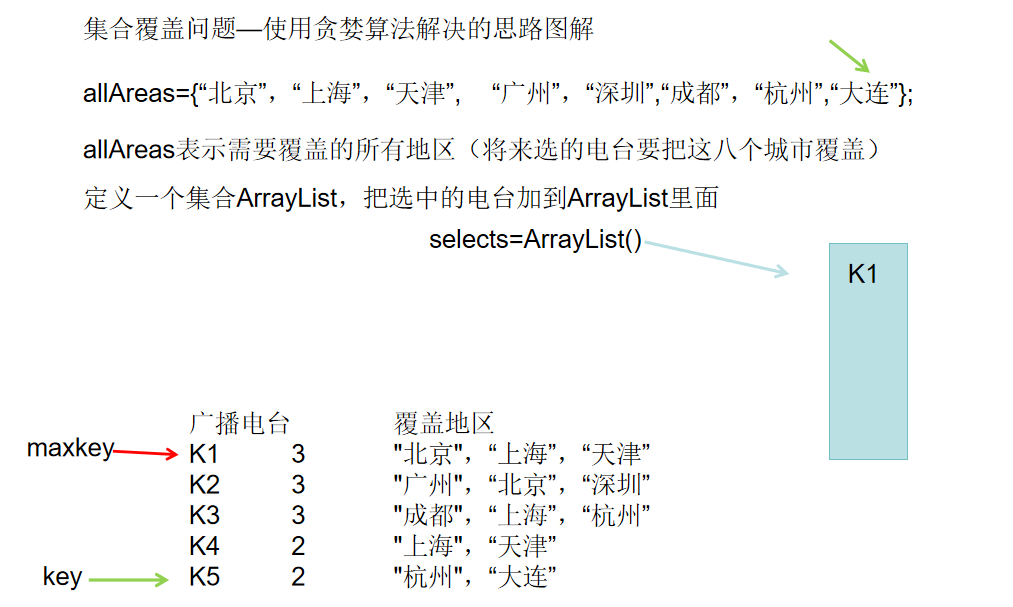
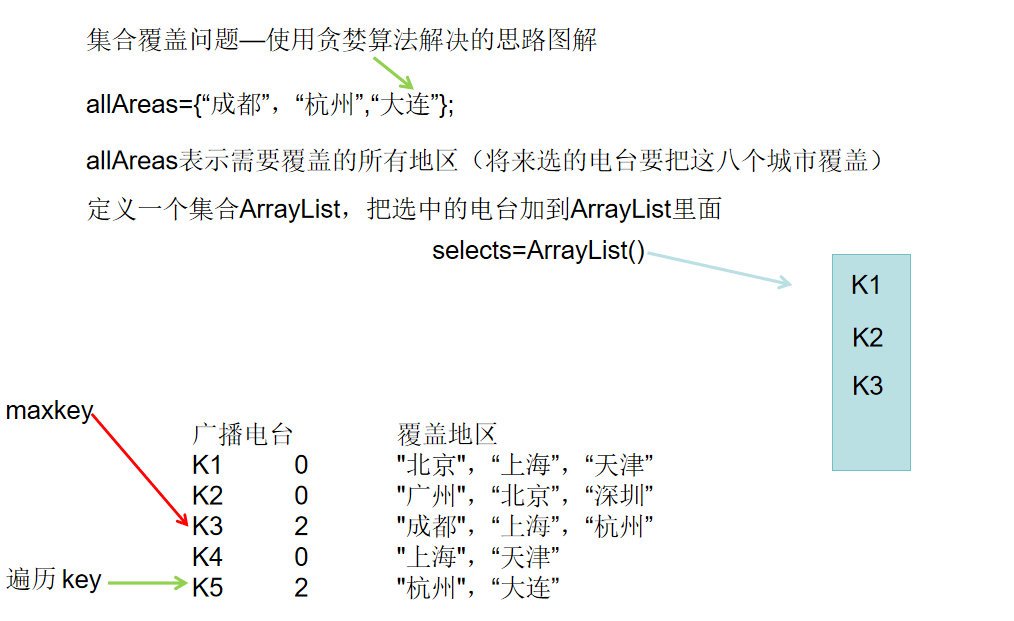
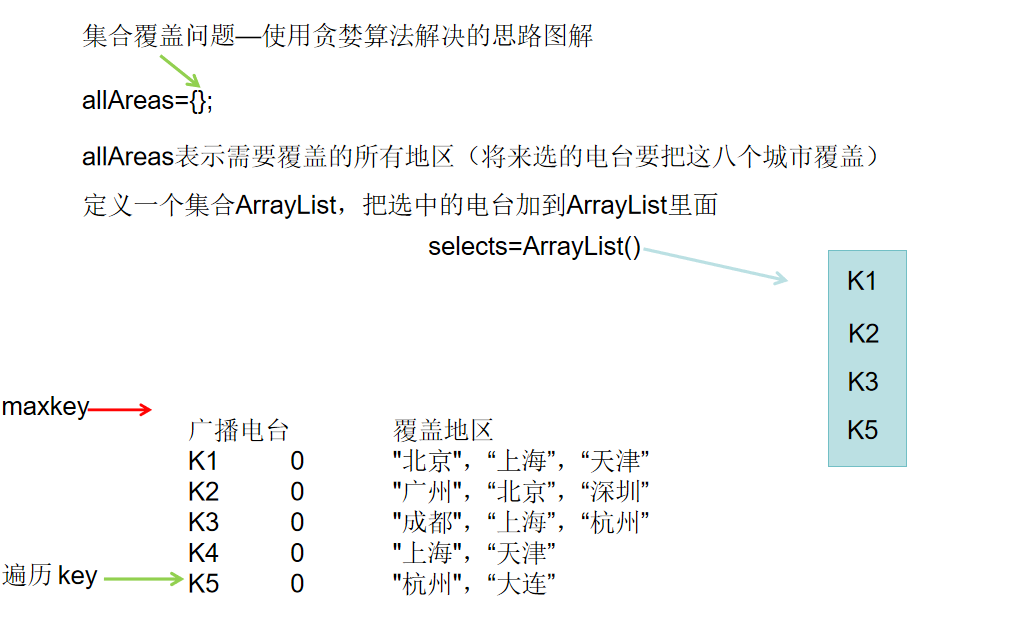
每次总是选一个能够覆盖最大未覆盖地区的电台，这就是贪心算法的体现（在遍历一轮的时候，我选最优的选择）

代码实现

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;namespace GreedyAlgorithm
{class Program{static void Main(string[] args){//创建存储广播电台的集合Dictionary<string, HashSet<string>> broadcasts = new Dictionary<string, HashSet<string>>();//创建广播电台和加入覆盖的地区HashSet<string> hashSet1 = new HashSet<string>();hashSet1.Add("北京");hashSet1.Add("上海");hashSet1.Add("天津");HashSet<string> hashSet2 = new HashSet<string>();hashSet2.Add("广州");hashSet2.Add("北京");hashSet2.Add("深圳");HashSet<string> hashSet3 = new HashSet<string>();hashSet3.Add("成都");hashSet3.Add("上海");hashSet3.Add("杭州");HashSet<string> hashSet4 = new HashSet<string>();hashSet4.Add("上海");hashSet4.Add("天津");HashSet<string> hashSet5 = new HashSet<string>();hashSet5.Add("杭州");hashSet5.Add("大连");//将各个电台放入到broadcastsbroadcasts.Add("K1", hashSet1);broadcasts.Add("K2", hashSet2);broadcasts.Add("K3", hashSet3);broadcasts.Add("K4", hashSet4);broadcasts.Add("K5", hashSet5);//allAreas存放所有的地区HashSet<string> allAreas = new HashSet<string>();allAreas.Add("北京");allAreas.Add("上海");allAreas.Add("天津");allAreas.Add("广州");allAreas.Add("深圳");allAreas.Add("成都");allAreas.Add("杭州");allAreas.Add("大连");//创建ArrayList,存放选择的电台集合ArrayList selects = new ArrayList();//定义一个临时的集合，在遍历的过程中，存放遍历过程中的电台覆盖的地区和当前还没有覆盖的地区的交集(key和allAreas的交集)HashSet<string> tempSet = new HashSet<string>();//定义maxKey,保存在一次遍历过程中，能覆盖最多未覆盖的地区的电台对应的key//如果maxKey不为null，则会加入到selectsstring maxKey = null;while (allAreas.Count != 0)  //如果allAreas不为0，则表示还没有覆盖到所有的地区，如果allArea为0，则表示selects里面选择的电台已经把所有的地区覆盖到了{//每进行一次while，需要将maxKey置空maxKey = null;//遍历broadcasts,取出电台对应的keyforeach (string key in broadcasts.Keys){//每进行一次for循环，需要将tempSet清空tempSet.Clear();//当前这个key能够覆盖的地区HashSet<string> areas = broadcasts[key];tempSet.UnionWith(areas);//求出tempSet和allAreas集合的交集,交集会赋给tempSettempSet.IntersectWith(allAreas);//如果当前这个集合包含的未覆盖地区的数量，比maxKey指向的集合还多//就需要重置maxKeyif (tempSet.Count>0 && (maxKey==null || tempSet.Count > broadcasts[maxKey].Count)){ //tempSet.Count>broadcasts[maxKey].Count 体现出贪心算法的特点，每次都选择最优的maxKey = key;}}// maxKey!=null,就应该将maxKey加入到selects集合中if (maxKey != null){selects.Add(maxKey);//将maxKey指向的广播电台覆盖的地区从allAreas中去掉//allAreas.Remove(Convert.ToString(broadcasts[maxKey])); allAreas.ExceptWith(broadcasts[maxKey]);}}foreach (var item in selects){Console.WriteLine(item.ToString());}}}
}