状压 dp --- TSP 问题

大家好，今天是 2025 年 9 月 5 日，我们继续开启状压 dp 的学习。

TSP 问题的题目问法和解决方案相对固定。

一：旅行商问题简介：

旅行商问题（Travelling salesman problem，TSP），是这样的一个问题：

给定 n 个城市以及每对城市之间的距离（完全图），求解访问每座城市一次且仅一次并回到起始位置城市的最短回路（哈密顿回路）（哈密顿图）。旅行商问题是一个 NP 完全问题，到目前为止没有多项式时间的高效算法。（不存在O（n），O（n * n），O（n * n * n）……等高效算法）。

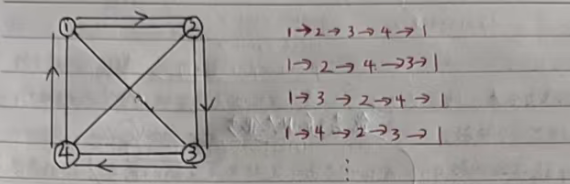
看到这个问题之后，我们首先肯定可以想到一个暴力解法：

我们可以暴力枚举 1~n 的全排列，根据每一种排列方式求出每一种路线的一个最短路。

但是，不幸的是，这样实现的话时间复杂度为 O（n * n!）n > 10 就会超时。

我们接下来的状压 dp 解法可以将时间复杂度优化到 O（n * n * 2^n）但是实际运行的时间是要远远小于这个数的，原因就是：我们在枚举状态的时候会有很多剪枝。因此 n > 20 才有可能超时。

二：旅行商问题模板题

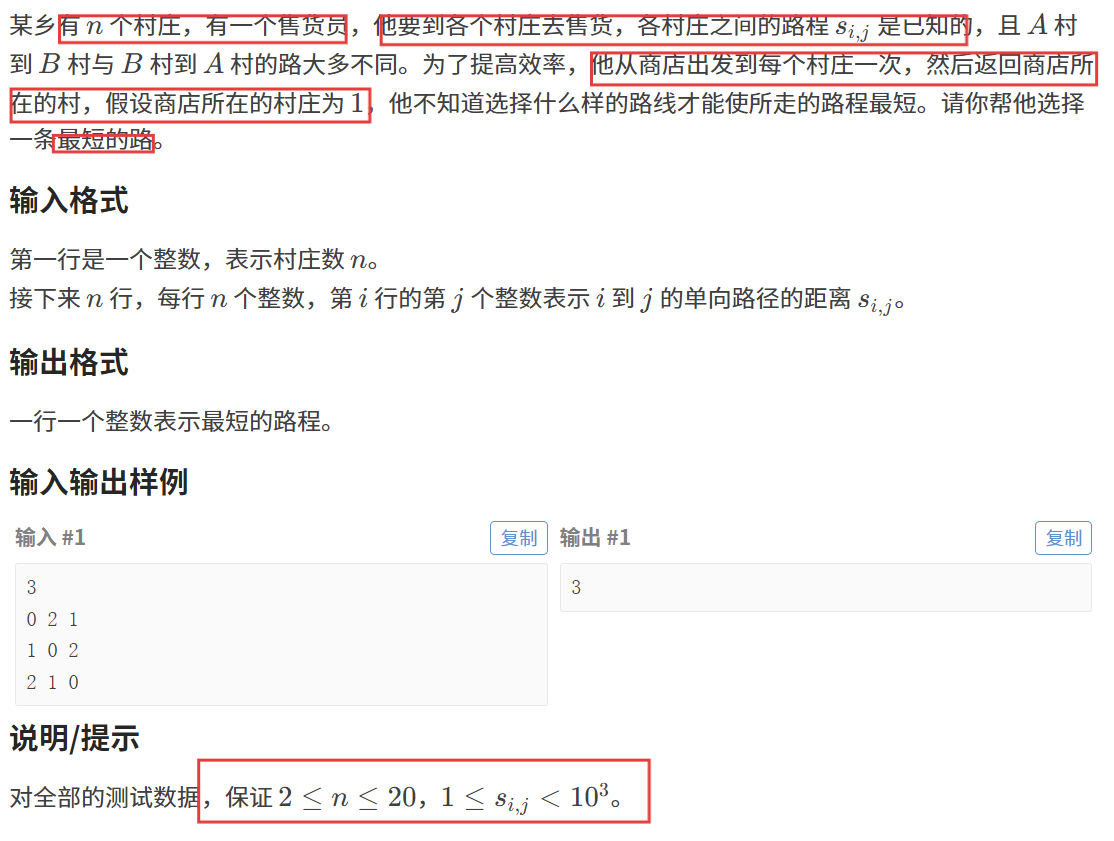
题目一：售货员的难题

题目链接：售货员的难题

【题目描述】

【算法原理】

通过读题，我们不难发现，这道题目就是给我们一个完全图，然后让我们求最短哈密顿回路。

扫一眼数据范围，显然我们可以尝试使用状压 dp 来解决这道问题。

我们首先先来暴力枚举一些路径，找一找规律：

我们发现，如果我们不考虑最后一步的话，其实就时从0号点出发，把所有的点都走一遍，此时的一个最短路。

1.状态表示

我们可以这样定义状态表示：

f[st][i]：表示从起点出发，每个点只能走一次，走过的点的状态为 st 时，最终落在 i 号点时的一个最短路。

2.最终结果

如果我们这样定义状态表示的话，结合题目要求，最终结果显然如下：

3.状态转移方程

推导状态转移方程时，我们要根据最近的一步来考虑问题：

假设我们现在在 i 号点位置，我们要枚举的是上一个点 j 的位置：

但是我们要保证走到 i 号点的路径中要包含 j 这个点：

那么我们就可以先走到 j 号点，再从 j 号点走向 i 号点。

4.初始化

因为我们要求的是最短路，因此所有的格子初始化为正无穷。

但是我们要从0号点开始出发，因此 f[1][0] = 0；

5.填表顺序

我们要从小到大枚举所有的状态，至于倒数第一个点和倒数第二个点的枚举顺序没有先后要求。

因为 st 中去除掉一个二进制中的 1 后，一定是小于 st 的。

【代码实现】

版本一：先枚举最后一个点，再枚举前面一个点

#include <iostream>
#include <cstring>using namespace std;const int N = 21;int n;
int e[N][N];int f[1 << N][N];int main()
{cin >> n;for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)cin >> e[i][j];memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int st = 2; st < (1 << n); st++)for(int i = 0; i < n; i++) // 枚举倒数第一个点 if((st >> i) & 1)for(int j = 0; j < n; j++) // 枚举倒数第二个点if((st >> j) & 1)f[st][i] = min(f[st][i], f[st ^ (1 << i)][j] + e[j][i]);int ret = 0x3f3f3f3f;for(int i = 1; i < n; i++) ret = min(ret, f[(1 << n) - 1][i] + e[i][0]);cout << ret << endl; return 0;
}

版本二：先枚举前面一个点，再枚举最后一个点

#include <iostream>
#include <cstring>using namespace std;const int N = 21;int n;
int e[N][N];int f[1 << N][N];int main()
{cin >> n;for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)cin >> e[i][j];memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int st = 2; st < (1 << n); st++)for(int j = 0; j < n; j++) // 枚举倒数第二个点if((st >> j) & 1)for(int i = 0; i < n; i++) // 枚举倒数第一个点 if((st >> i) & 1)f[st][i] = min(f[st][i], f[st ^ (1 << i)][j] + e[j][i]);int ret = 0x3f3f3f3f;for(int i = 1; i < n; i++) ret = min(ret, f[(1 << n) - 1][i] + e[i][0]);cout << ret << endl; return 0;
}

最后解释一个问题：上述代码中，是如何保证所有的点仅仅只走一次的？？？

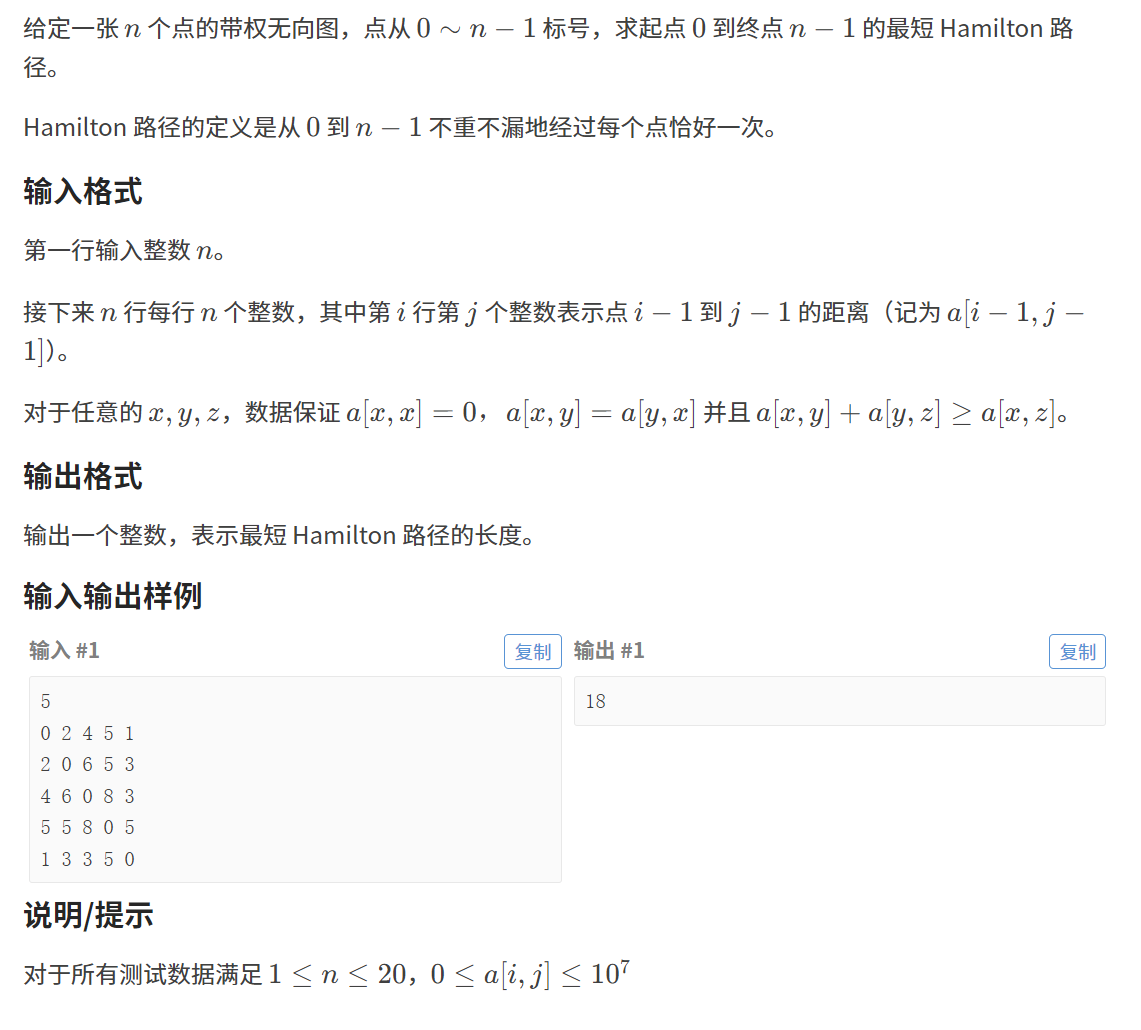
题目二：最短 Hamilton 路径

题目链接：最短 Hamilton 路径

本题是一个二倍经验的题目，题目和上一题几乎一模一样，因此这里只给出代码实现。

【代码实现】

#include <iostream>
#include <cstring>using namespace std;const int N = 21;int n;
int e[N][N];
int f[1 << N][N];int main()
{cin >> n;for(int i = 0; i < n; i++)for(int j = 0; j < n; j++)cin >> e[i][j];memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int st = 2; st < (1 << n); st++)for(int i = 0; i < n; i++)if((st >> i) & 1)for(int j = 0; j < n; j++)if((st >> j) & 1)f[st][i] = min(f[st][i], f[st ^ (1 << i)][j] + e[j][i]);cout << f[(1 << n) - 1][n - 1] << endl;return 0;
} 

好的，今天的分享就到这里了。谢谢大家！！！