数据结构堆树java版本实现（大顶堆）

堆的定义

1.满足完全二叉树的特性（除了最后一层外，每层节点都是满的；最后一层的节点从左到右连续排列。）
2.分为大顶堆和小顶堆（1）大顶堆：每个节点的值 ≥ 左右子节点的值 → 堆顶是最大值。（2）小顶堆：每个节点的值 ≤ 左右子节点的值 → 堆顶是最小值。

堆的建立过程

概述：
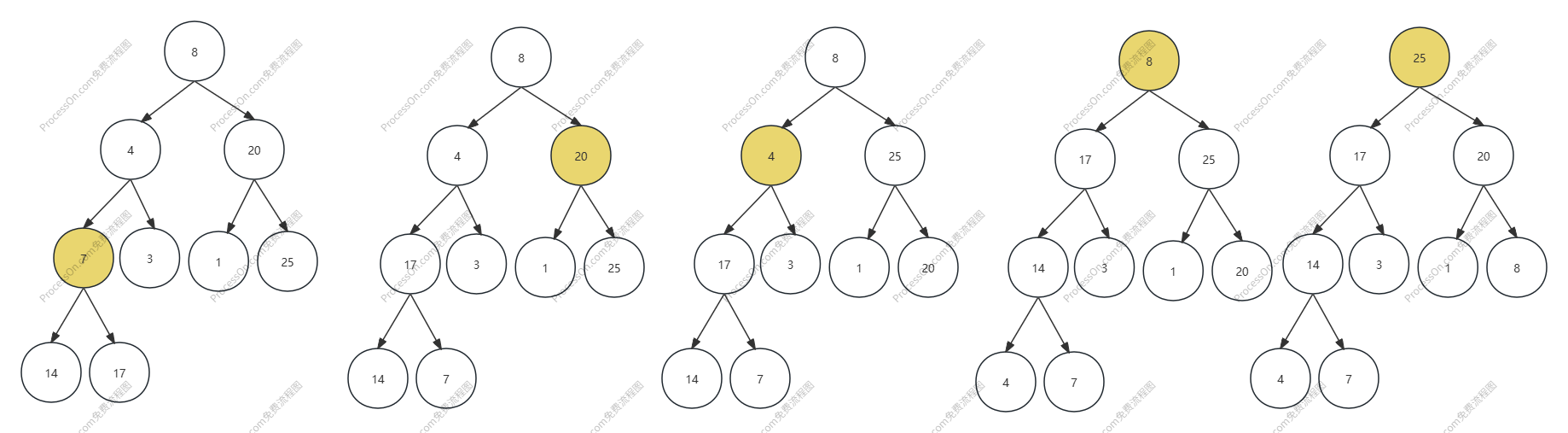
从最后一个非叶子节点开始堆化，从后往前，依次是7,20,4,8，为什么顺序看着是蛇形走位呢。
因为这是数组存储，8相当于索引0位置，4为索引1的位置，20相当于索引2的位置，
7相当于索引3的位置，依次类推.....,看着像是蛇形走位，其实就是从后面的索引往前比对

堆的排序过程

排序策略，将堆顶元素和最后一个元素交换，交换完成后进行一次下沉堆化操作，依次执行操作即可，
但是已经交换过的堆顶元素不需要再参与下沉堆化操作，因为默认堆顶元素就是最大的数字，
交换位置后本来就是最大的数字了，参与堆化无意义，也不能保证排序了。
（要明白在大顶堆中，堆顶的肯定是最大的，一次次结尾的与堆顶的交换，很显然顺序就出来了，
就跟小学课本高斯解1到100那个问题一样，只不过这块是交换，第一个与倒数第一个交换，
第二个与倒数第二个交换，以此类推，直到排序完成）

具体代码实现

package com.che.datajg;import java.util.Arrays;/*** @Author Cyh* @PackageName:com.che.datajg 堆树*/
public class HeapTree {public static void main(String[] args) {int[] a = {8, 4, 20, 7, 3, 1, 25, 14,17,2,100,54,67,89,32,8};heapSort(a);}/*** 创建大顶堆* 大顶堆的特点：每个节点的值都大于其左右子节点的值，满足完全二叉树的特性* 完全二叉树：除了最后一层外，其他层都是满的，最后一层的节点都靠左排列* @param data  数组元素* @param length 数组长度*/public static void maxHeap(int[] data, int length)  {for (int i = length / 2 - 1; i >= 0; i--) {//进行堆化操作heapify(data, i, length);}System.out.println("创建大顶堆："+Arrays.toString(data));}/*** 堆化操作* @param data   数组元素* @param index   要进行交换的元素索引* @param length  数组长度*/public static void heapify(int[] data, int index, int length) {int a = index;int temp = data[a]; // 先存下来，避免频繁交换int leftIndex = a * 2 + 1;// 这个判断是为了防止数组越界// 为什么不判断右节点呢？//1.完全二叉树特性，如果左节点越界，那么右节点肯定越界//2.判断右节点的话还有可能出现如果整棵树中最后一层只有一个左节点的话,// 由于判断的是右节点,不会进入循环,就会忽略这个左节点,导致堆化错误.while (leftIndex < length) {int rightIndex = leftIndex + 1;// 选出更大的子节点（相等时固定选右孩子）int biggerIndex = leftIndex;//判断右节点数组越界,同时又判断了右节点是否大于左节点,选出最大的子节点if (rightIndex < length && data[rightIndex] >= data[leftIndex]) {biggerIndex = rightIndex;}// 如果子节点比父节点大，则下沉if (data[biggerIndex] > temp) {data[a] = data[biggerIndex];// 更新父节点索引,继续while循环是否还需要继续下沉leftIndex = biggerIndex * 2 + 1;} else {break;}}data[a] = temp;}/*** 堆排序* @param data  数组元素*/public static void heapSort(int[] data) {//首先将数组构造成大顶堆，这样数组中最大的元素就会被放到数组的第一个位置maxHeap(data,data.length);//接下来就是交换顶节点和尾节点元素，将最大元素排在尾部（这就是最大的，这是大顶堆特性）//交换之后对新的顶节点进行堆下沉操作，使其满足大顶堆特性//循环以上两步操作，先顶节点和尾节点交换，再对顶节点进行堆下沉操作，直到所有元素都排好序int length = data.length;for (int i = length-1; i > 0; i--) {int max=data[0];int end=data[i];data[0]=end;data[i]=max;heapify(data,0, i);}System.out.println("最终排序结果："+Arrays.toString(data));}
}