数据结构初阶:树的相关性质总结
🔥个人主页:胡萝卜3.0
🎬作者简介:C++研发方向学习者
📖个人专栏: 《C语言》、《数据结构》 、《C++干货分享》、LeetCode&牛客代码强化刷题
⭐️人生格言:不试试怎么知道自己行不行


目录
一、通用性质
二、树形结构
三、二叉树的性质编辑
3.1 特殊的二叉树
3.1.1 满二叉树的性质
3.1.2 完全二叉树的性质
3.2 二叉树的顺序结构——堆的性质
3.2.1 二叉树的性质(堆中使用)
一、通用性质
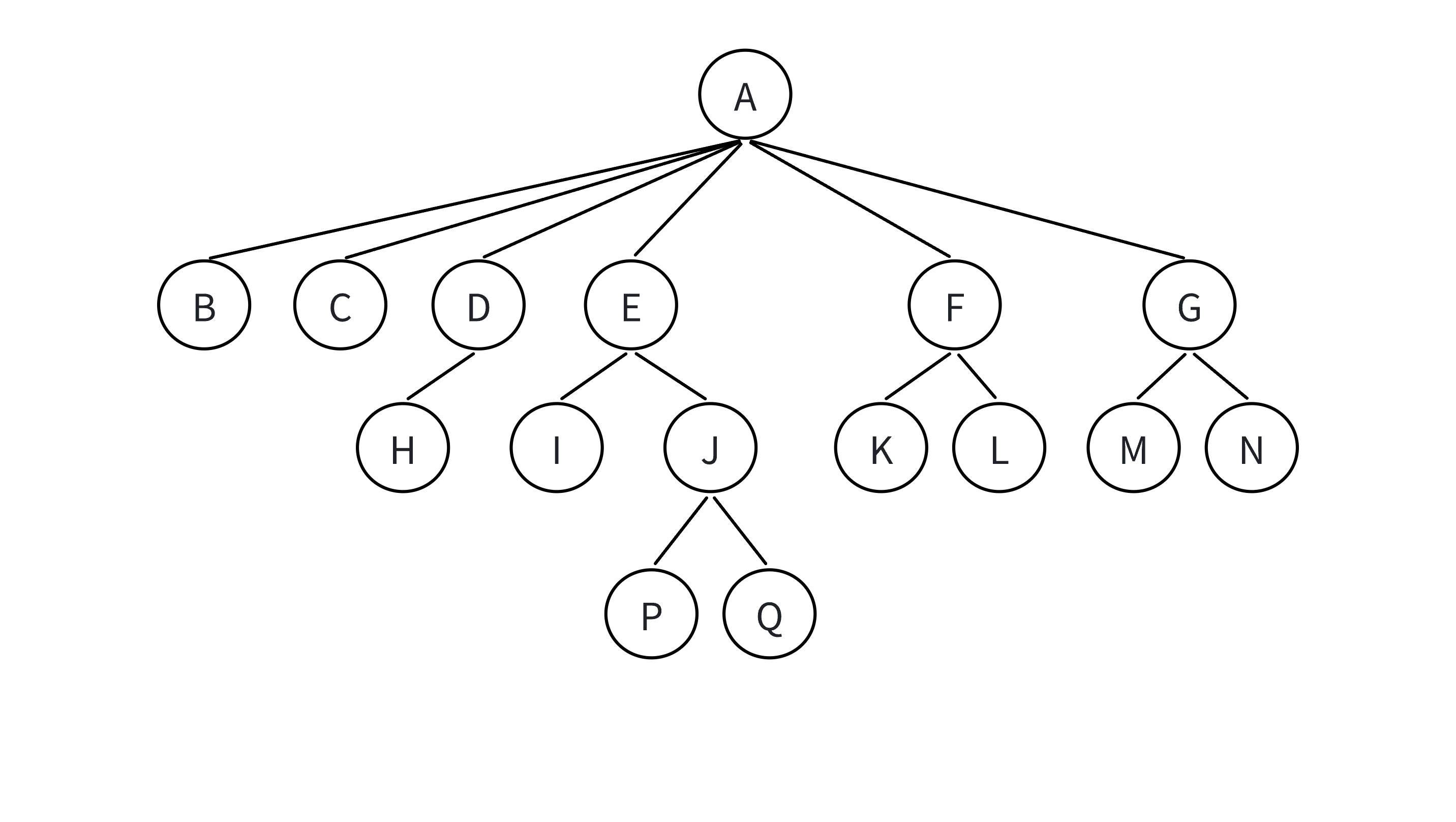
1、有且仅有一个根节点:根节点是树的最顶层结点。没有父节点
2、子节点与父节点:除了根节点外,其余每个节点都有且仅有一个父节点,一个父节点可以有0个或多个子节点。
3、兄弟节点:具有相同父节点的节点称为兄弟节点。
4、祖先和子孙:从根节点或该节点路径上所经过的所有节点都是其祖先,以某节点为根的子树中的所有节点都是其子孙。
5、度:
- 节点的度:一个节点拥有的子节点数目。
- 树的度:树中所有节点的度的最大值。
6、层次:根节点的层次为1,根节点的孩子节点的层次为2,……以此类推。
7、树的深度/高度:树中节点的最大层次。
8、叶子节点:度为0的节点。
9、分支节点:度不为0的节点。
10、子树:每个节点及其所有子孙组成一个树。树是由根节点和若干棵互不相交的子树构成。
二、树形结构
1、子树是不相交的(如果子树存在相交,就是图)
2、除了根节点,每个节点都仅有一个父节点
3、一棵树有N个节点,则有N-1条边。(2个节点,1条边)
三、二叉树的性质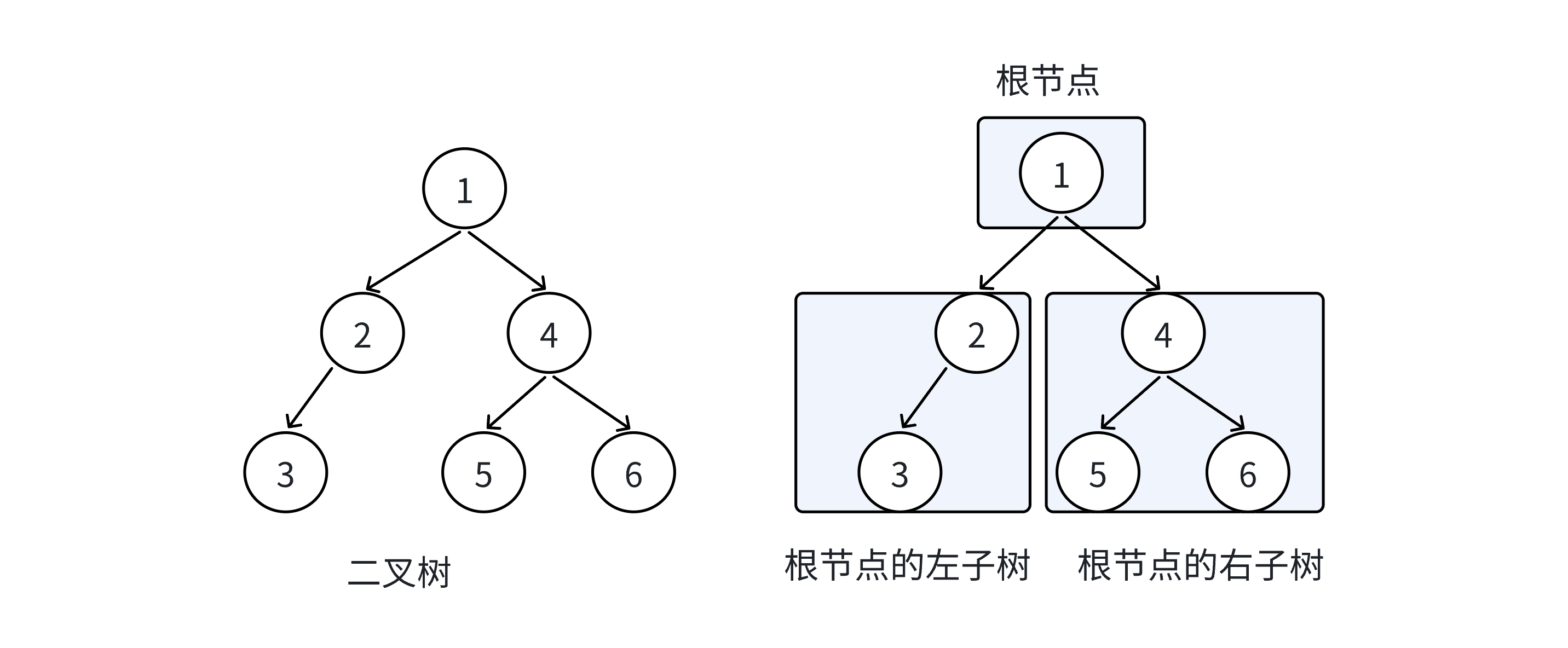
- 二叉树中不存在度大于2的节点。
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
- 对于任何一棵二叉树,如果度为0其叶子节点个数为n0,度为2的分支节点个数为n2,则有n0=n2+1。
3.1 特殊的二叉树
3.1.1 满二叉树的性质
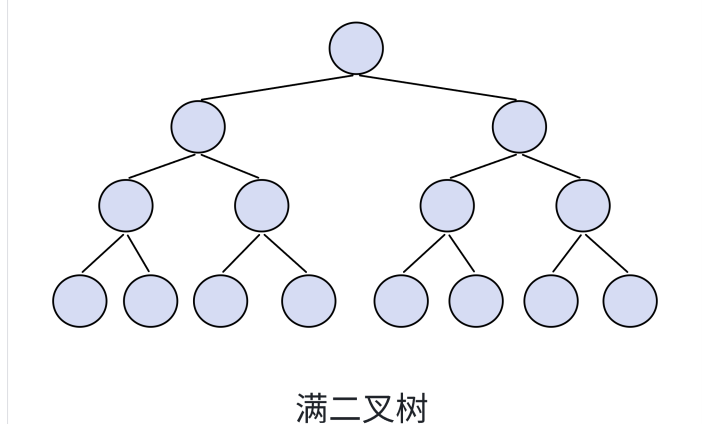
- 树的度为2,即最大节点个数为2。
- 每一层节点个数都达到最大,假设层数为k,则每层节点个数为2^(k-1),节点总数为2^k-1。
根据满二叉树的性质可知:
1、若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个节点。
2、若规定根节点的层数为1,则深度为h的二叉树的最大节点个数为2^h-1。
3、若规定根节点的层数为1,具有n个节点的满二叉树的深度为h=log2(n+1)(log以2为底,n+1的对数)。
3.1.2 完全二叉树的性质
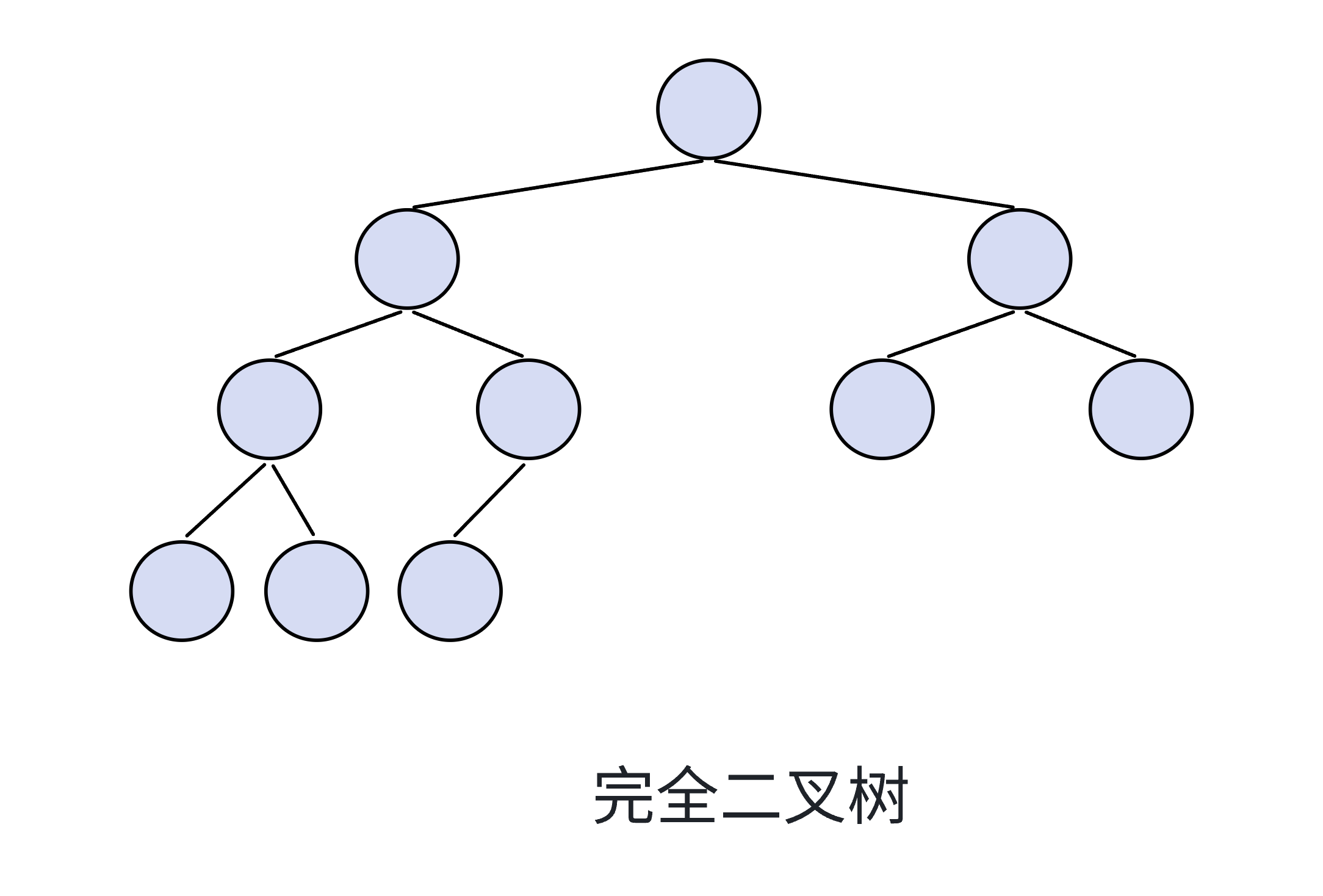
- 除了最后一层,其余每层节点个数都达到最大,最后一层节点个数不一定达到最大。
- 节点是从左往右依次排序的(先有左孩子,才有右孩子,否则就不是完全二叉树)。
- 在完全二叉树中,度为1的节点个数有1个或者0个。
- 完全二叉树的节点个数=度为0的节点个数+度为1的节点个数+度为2的节点个数。
根据完全二叉树和满二叉树的性质可知——
最后一层节点个数<=2^(h-1)。
3.2 二叉树的顺序结构——堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值(若堆中的某个节点的值总是不大于其父节点的值为大堆;若堆中的某个节点的值总是不小于其父节点的值为小堆)。
- 堆总是一棵完全二叉树
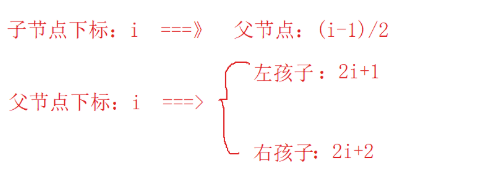
3.2.1 二叉树的性质(堆中使用)