直线与椭圆相交弦长计算公式
直线与椭圆相交弦长计算公式
说明:本文并非我原创,该定理为硬解定理,多参考书已有,只是我在学习写论文,以此为例而已。
文章目录
- 直线与椭圆相交弦长计算公式
- 摘要
- 计算任意直线与中心在原点的椭圆相交弦长
- 利用线性变换计算任意直线与任意椭圆相交弦长
- 更一般的二次曲线相交弦弦长公式
- 结果与结果分析
- 结果
- 结果分析
摘要
针对直线与椭圆相交弦长的计算问题,本文采用一元二次方程求根公式,推导得出标准椭圆与任意直线相交的弦长计算公式。研究进一步发现:其一,通过韦达定理可以减少一部分计算;其二,通过等距变换,可将该方法推广至一般二次曲线,得到其与直线相交的弦长计算公式。此外,本文研究存在一定局限性:结合仿射变换与二次型理论,可将高中阶段相关题型拓展至更普遍的二次型理论框架,进而推导得出相应通用定理。
计算任意直线与中心在原点的椭圆相交弦长
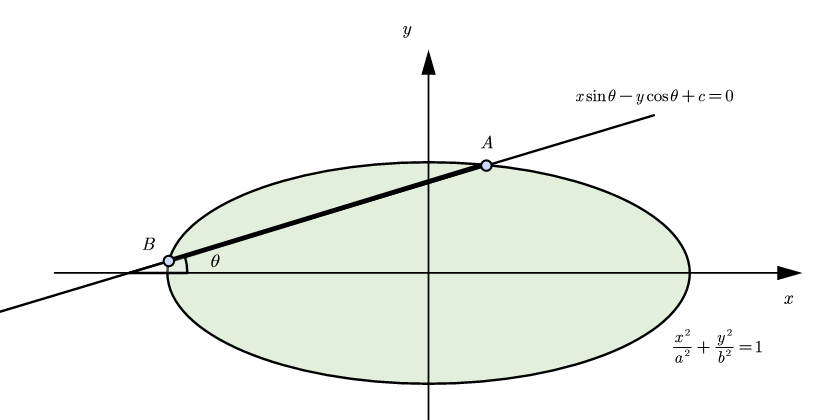
如图1,表示一个与xxx轴夹角为θ\thetaθ的直线:xsinθ−ycosθ+c=0x\sin \theta -y\cos \theta +c=0xsinθ−ycosθ+c=0
与焦点在xxx轴上的椭圆:x2a2+y2b2=1\frac{x^2}{a^2}+\frac{y^2}{b^2}=1a2x2+b2y2=1相交于A(xA,yA)A\left( x_A,y_A \right)A(xA,yA)、B(xB,yB)B\left( x_B,y_B \right)B(xB,yB)两点的示意图。
要求解相交弦的长度,首先要求出AAA、BBB两点的坐标。联立直线与椭圆的方程:
{xsinθ−ycosθ+c=0x2a2+y2b2=1\begin{cases} x\sin \theta -y\cos \theta +c=0\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \end{cases} {xsinθ−ycosθ+c=0a2x2+b2y2=1
消去yyy得到二元一次方程组:
(b2cos2θ+a2sin2θ)x2+2a2csinθ⋅x+(a2c2−a2b2cos2θ)=0(b^2\cos^2\theta + a^2\sin^2\theta)x^2 + 2a^2c\sin\theta \cdot x + (a^2c^2 - a^2b^2\cos^2\theta) = 0(b2cos2θ+a2sin2θ)x2+2a2csinθ⋅x+(a2c2−a2b2cos2θ)=0
当判别式大于000时,计算弦长为:
∣AB∣=(xA−xB)2+(yA−yB)2=1+tan2θ(xA+xB)2−4x1x2=2aba2sin2θ+b2cos2θ−c2b2cos2θ+a2sin2θ\begin{align*} |AB|&=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}\\ &=\sqrt{1+\tan^2\theta}\sqrt{\left(x_A+x_B\right)^2-4x_1x_2}\\ &=\frac{2ab\sqrt{a^2\sin^2\theta + b^2\cos^2\theta - c^2}}{b^2\cos^2\theta + a^2\sin^2\theta} \end{align*}∣AB∣=(xA−xB)2+(yA−yB)2=1+tan2θ(xA+xB)2−4x1x2=b2cos2θ+a2sin2θ2aba2sin2θ+b2cos2θ−c2
利用线性变换计算任意直线与任意椭圆相交弦长
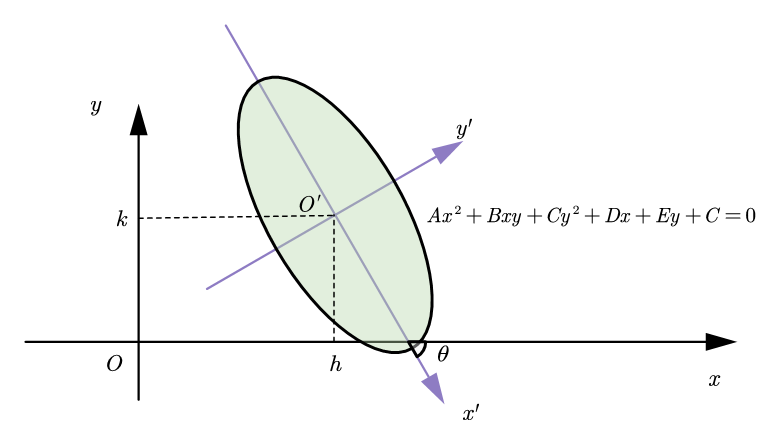
如图2展示了:对于一般的二次曲线Γ\GammaΓ:Ax2+Bxy+Cy2+Dx+Ey+C=0Ax^2+Bxy+Cy^2+Dx+Ey+C=0Ax2+Bxy+Cy2+Dx+Ey+C=0在坐标系中的情况,其长轴所在的直线与xxx轴的夹角为θ\thetaθ。由于标准二次曲线处理起来较为简单,由此考虑先绕中心坐标(h,k)(h,k)(h,k)逆时针旋转θ\thetaθ的角度然后平移到坐标原点得到中心落在坐标原点的标准二次曲线,变化矩阵如下:
(x′y′1)=(cosθ−sinθhsinθcosθk001)(xy1)\begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta & h \\ \sin\theta & \cos\theta & k \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} x′y′1=cosθsinθ0−sinθcosθ0hk1xy1
由此,只要分析中心落在坐标原点的标准二次曲线即可。
更一般的二次曲线相交弦弦长公式
对于直线LLL:Ax+By+C=0Ax+By+C=0Ax+By+C=0与二次曲线Γ\GammaΓ:x2m+y2n=1\frac{x^2}{m}+\frac{y^2}{n}=1mx2+ny2=1,
同理联立两个方程可以得到:
(nB2+mA2)x2+2mACx+m(C2−nB2)=0\left(nB^2+mA^2\right)x^2+2mACx+m\left(C^2-nB^2\right)=0 (nB2+mA2)x2+2mACx+m(C2−nB2)=0
不难得到,当4mn(nB2+mA2−C2B2)>04mn\left(nB^2+mA^2-C^2B^2\right)>04mn(nB2+mA2−C2B2)>0存在两个交点:
x1,2=−mAC±mn(nB2+mA2−C2)(nB2+mA2)x_{1,2}=\frac{- mAC\pm \sqrt{mn\left(nB^2+mA^2-C^2\right)}}{\left(nB^2+mA^2\right)}x1,2=(nB2+mA2)−mAC±mn(nB2+mA2−C2)
或由韦达定理:
{x1+x2=−2mACnB2+mA2x1x2=m(C2−nB2)nB2+mA2\begin{cases} x_1+x_2=-\frac{2mAC}{nB^2+mA^2}\\ x_1x_2=\frac{m\left(C^2-nB^2\right)}{nB^2+mA^2} \end{cases}{x1+x2=−nB2+mA22mACx1x2=nB2+mA2m(C2−nB2)
相交弦的长度为:
∣AB∣=1+(AB)2(−2mACnB2+mA2)2−4⋅m(C2−nB2)nB2+mA2|AB|=\sqrt{1+\left(\frac{A}{B}\right)^2}\sqrt{\left(-\frac{2mAC}{nB^2+mA^2}\right)^2-4\cdot\frac{m\left(C^2-nB^2\right)}{nB^2+mA^2}}∣AB∣=1+(BA)2(−nB2+mA22mAC)2−4⋅nB2+mA2m(C2−nB2)
化简得到:
∣AB∣=2mn(A2+B2)(mA2+nB2−C2)nB2+mA2\boxed{|AB| = \frac{2\sqrt{mn(A^2 + B^2)(mA^2 + nB^2 - C^2)}}{nB^2 + mA^2}}∣AB∣=nB2+mA22mn(A2+B2)(mA2+nB2−C2)
结果与结果分析
结果
| 项目 | 椭圆Γ:x2m+y2n=1\Gamma: \frac{x^2}{m} + \frac{y^2}{n} = 1Γ:mx2+ny2=1(m>0,n>0m > 0, n > 0m>0,n>0) | 双曲线Γ:x2m+y2n=1\Gamma: \frac{x^2}{m} + \frac{y^2}{n} = 1Γ:mx2+ny2=1(m>0,n<0m > 0, n < 0m>0,n<0 或 m<0,n>0m < 0, n > 0m<0,n>0) |
|---|---|---|
| x1+x2x_1 + x_2x1+x2 | −2mACnB2+mA2\boxed{-\dfrac{2mAC}{nB^2 + mA^2}}−nB2+mA22mAC | −2mACnB2+mA2\boxed{-\dfrac{2mAC}{nB^2 + mA^2}}−nB2+mA22mAC |
| x1x2x_1x_2x1x2 | m(C2−nB2)nB2+mA2\boxed{\dfrac{m(C^2 - nB^2)}{nB^2 + mA^2}}nB2+mA2m(C2−nB2) | m(C2−nB2)nB2+mA2\boxed{\dfrac{m(C^2 - nB^2)}{nB^2 + mA^2}}nB2+mA2m(C2−nB2) |
| 判别式Δ\DeltaΔ | 4mnB2(mA2+nB2−C2)\boxed{4mnB^2(mA^2 + nB^2 - C^2)}4mnB2(mA2+nB2−C2)(mn>0mn > 0mn>0) | 4mnB2(mA2+nB2−C2)\boxed{4mnB^2(mA^2 + nB^2 - C^2)}4mnB2(mA2+nB2−C2)(mn<0mn < 0mn<0) |
| 相交条件 | Δ>0⟹mA2+nB2>C2\Delta > 0 \implies mA^2 + nB^2 > C^2Δ>0⟹mA2+nB2>C2 | Δ>0⟹mA2+nB2−C2<0\Delta > 0 \implies mA^2 + nB^2 - C^2 < 0Δ>0⟹mA2+nB2−C2<0(因mn<0mn < 0mn<0,不等号方向反转) |
| 弦长 (|AB|) | 2mn(A2+B2)(mA2+nB2−C2)nB2+mA2\boxed{\dfrac{2\sqrt{mn(A^2 + B^2)(mA^2 + nB^2 - C^2)}}{nB^2 + mA^2}}nB2+mA22mn(A2+B2)(mA2+nB2−C2) | 2∣mn∣(A2+B2)(C2−mA2−nB2)nB2+mA2\boxed{\dfrac{2\sqrt{|mn|(A^2 + B^2)(C^2 - mA^2 - nB^2)}}{nB^2 + mA^2}}nB2+mA22∣mn∣(A2+B2)(C2−mA2−nB2) |
结果分析
令A=sinθA=\sin \thetaA=sinθ、$B=\cos \theta 、、、C=c、、、m=a2$和$n=b2$。代入推广结论得到:
∣AB∣=2aba2sin2θ+b2cos2θ−c2b2cos2θ+a2sin2θ|AB|=\frac{2ab\sqrt{a^2\sin^2\theta + b^2\cos^2\theta - c^2}}{b^2\cos^2\theta + a^2\sin^2\theta}∣AB∣=b2cos2θ+a2sin2θ2aba2sin2θ+b2cos2θ−c2
这与第一部分求解得到的结论是一样的,由此可验证结论的正确性。
