LeetCode 142.环形链表 II
目录
- 1 题目概述
- 2 题目解法
- 3 证明
原题链接
环形链表 II
前言
在做这道题目之前,应该先做一次 环形链表 I 和 相交链表,这样对这道题目中所使用的方法会有较深的理解
1 题目概述
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 不允许修改链表。
示例1:

使用指针来遍历这个链表的时候,指针会不断地在 2,0,-4 三个结点处打转,这就说明链表内是有环的,而我们要做的事情,就是返回环的第一个结点 2
示例2:

在遍历这个链表时,指针不会在结点中打转,因此它并不存在环,也不存在环的第一个结点,返回空即可
2 题目解法
在解这道题目时,我们需要进行两个操作,判断链表中是否有环和找出环内的第一个结点
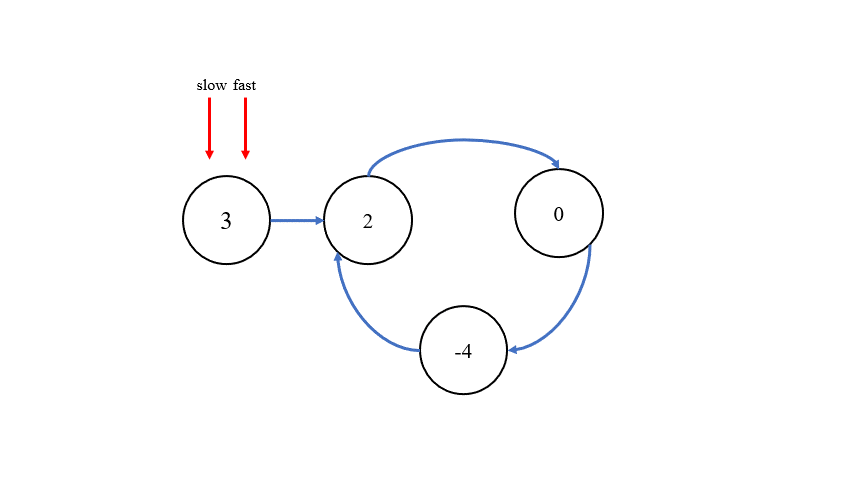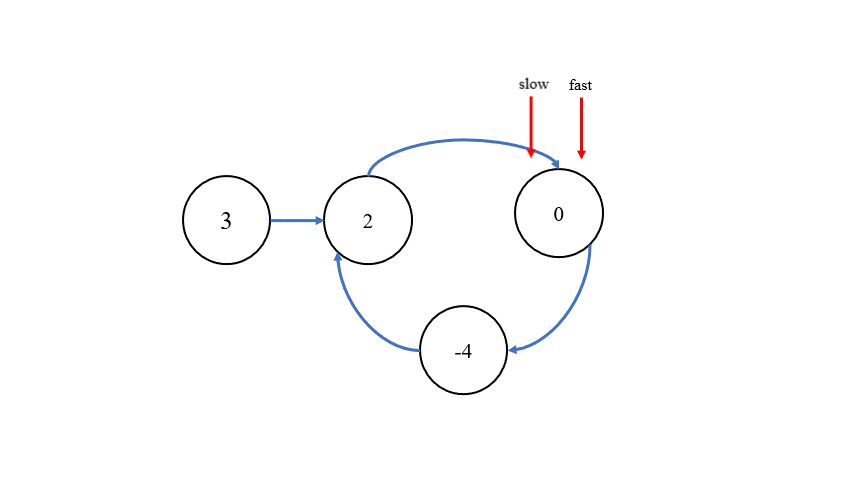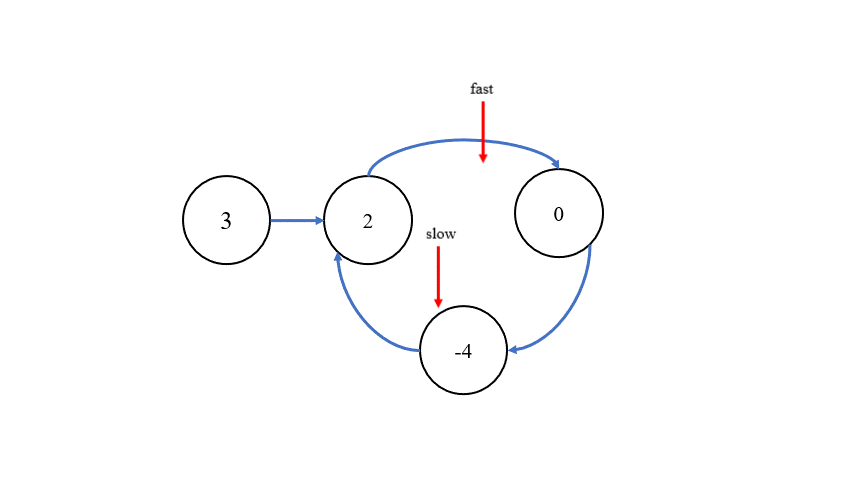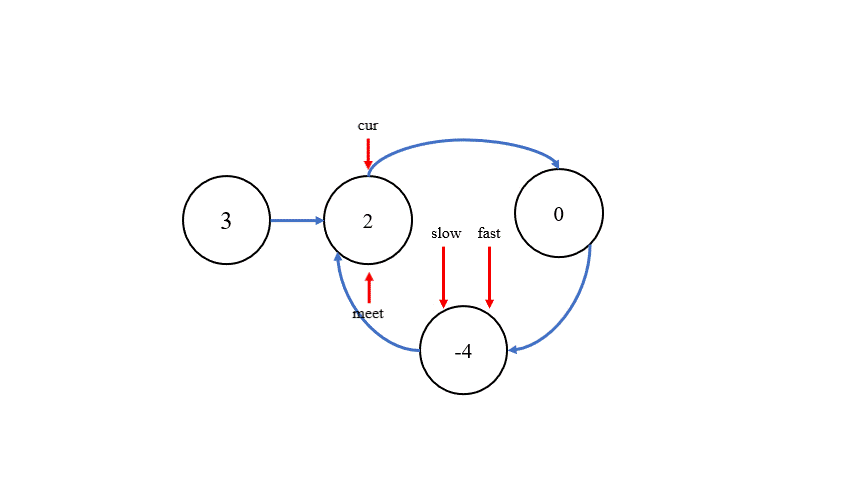
判断链表中是否有环的办法,与 环形链表 I 一致,采用快慢指针来判断,快指针一次走两步,慢指针一次走一步,当快慢指针相遇,则说明有环。
找出环内的第一个结点则有两种方法,第一种方法是,在快慢指针相遇的位置设定新指针 meet,在链表的头部设定指针 cur,让两个指针同时移动,每次移动一步,当它们相遇时,就可以找到环内的第一个结点。第二种方法则是,当快慢指针相遇时,将它们所指向的下一个结点记录为nextNode,将指向的本结点的 next 指针断开,构造出两个链表,再找两个链表公共部分的第一个结点即可。接下来,对两个方法进行图示说明:
第一种方法
第二种方法
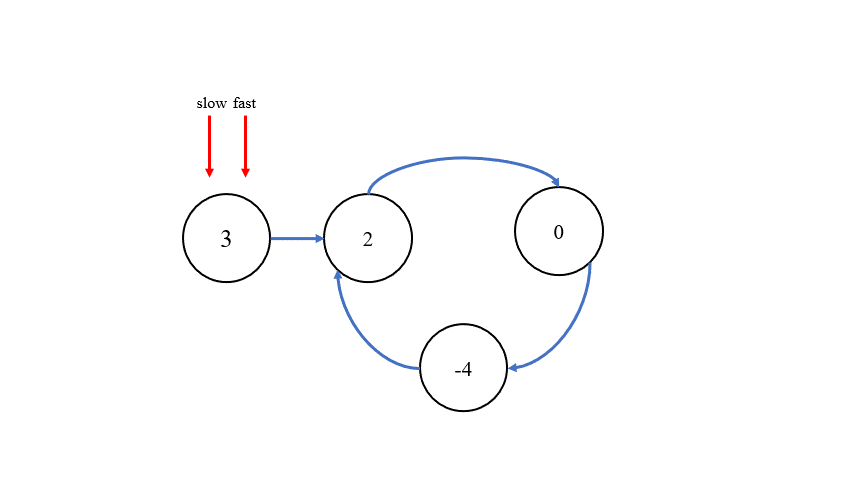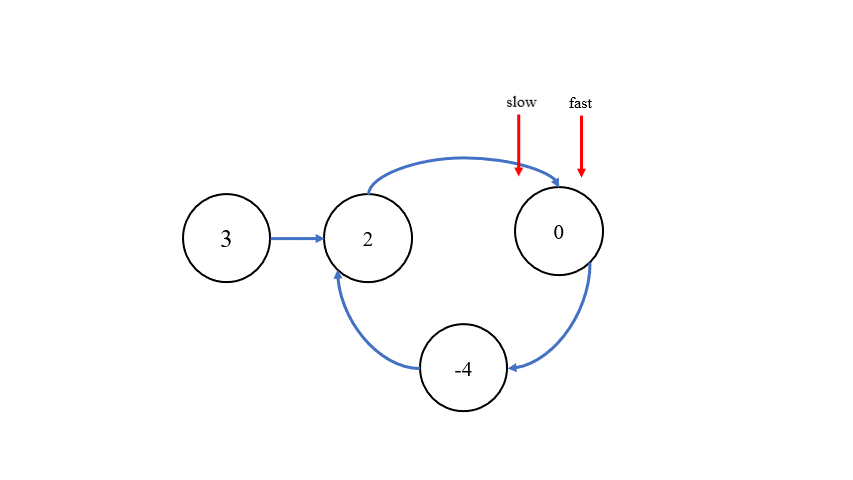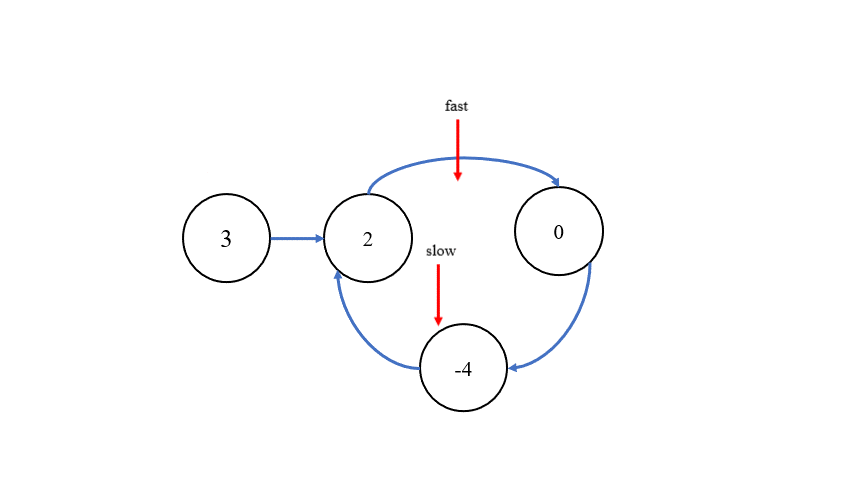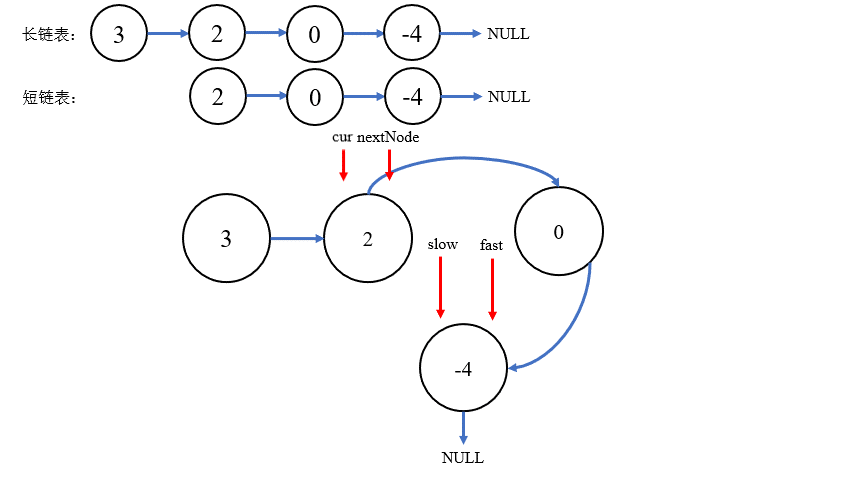
在断开并产生两个链表后,先遍历较长链表,使其剩下的长度等于短链表,再同时遍历,直到指针相遇,就可以找到相交的结点
代码如下
//方法1
struct ListNode* detectCycle(struct ListNode* head)
{ListNode* slow = head;ListNode* fast = head;//判断是否有环while (fast && fast->next){slow = slow->next;fast = fast->next->next;if (slow == fast){ListNode* cur = head;ListNode* meet = slow;//找入环第一个结点while (cur != meet){cur = cur->next;meet = meet->next;}return cur;}}return NULL;
}//方法2
ListNode* getCrossNode(ListNode* ListA, ListNode* ListB)
{ListNode* curA = ListA;ListNode* curB = ListB;int lenA = 0;int lenB = 0;while (curA){lenA++;curA = curA->next;}while (curB){lenB++;curB = curB->next;}//假设法int k = abs(lenA - lenB);ListNode* longList = ListA;ListNode* shortList = ListB;if (lenB > lenA){longList = ListB;shortList = ListA;}//部分遍历长链表while (k--){longList = longList->next;}//同时遍历while (shortList != longList){shortList = shortList->next;longList = longList->next;}return shortList;
}struct ListNode* detectCycle(struct ListNode* head)
{ListNode* slow = head;ListNode* fast = head;//判断是否有环while (fast && fast->next){slow = slow->next;fast = fast->next->next;//拆分链表if (slow == fast){ListNode* nextNode = slow->next;slow->next = NULL;return getCrossNode(head, nextNode);}}return NULL;
}
3 证明
为什么让 meet 指针从 slow 和 fast 相遇的位置开始走,让 cur 从头开始走一定能够相遇呢?
假设现在有一个链表,在这个链表中,slow 刚进入环,指向入环的第一个结点,而 fast 已经在环内走了一段距离
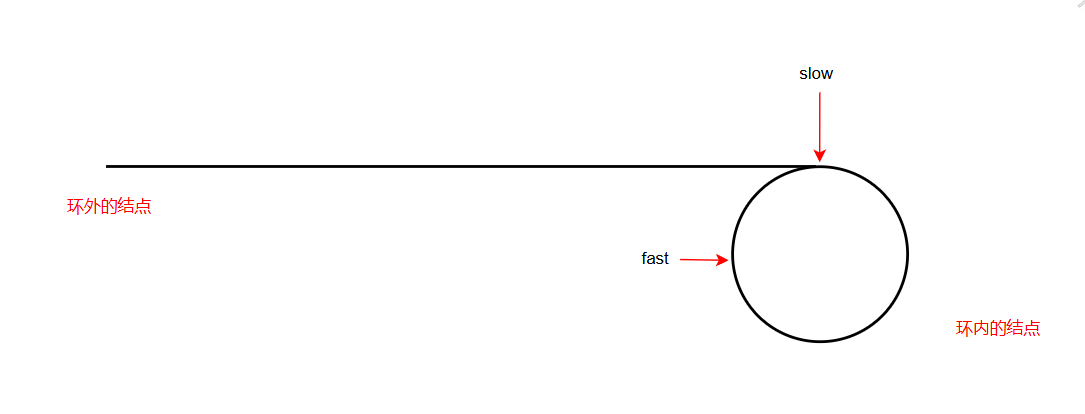
继续移动,直到 fast 和 slow 相遇。在此将链表起始位置到入环第一个结点的距离设为 L,slow 入环后走的距离为 N,环的一圈距离为 C,走过的圈数为 x
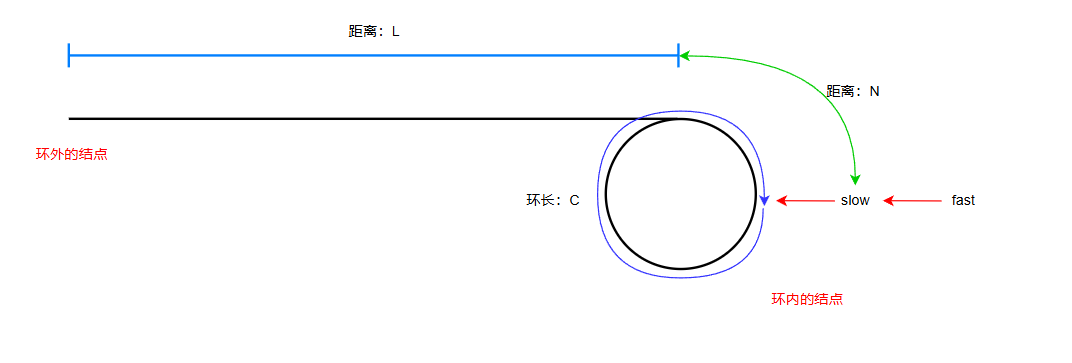
在这个情况下,slow 走的距离为 L + N,fast 走过的距离为 L + x * C + N (x ≠ 0)
x ≠ 0 是因为,fast 的速度是 slow 的两倍,当 slow 和 fast 相遇时,fast 至少走过了一圈
由于 fast 和 slow 走的时间相同,fast 的速度是 slow 的两倍,因此 fast 走过的距离是 slow 的两倍,我们可以得到 2 (L + N) = L + x * C + N
对这个式子进行化简,最终会得到 L = x * C - N
当 x 取 1 时,L = C - N,也就是说明,从相遇的位置开始到入环第一个结点的距离 和 从链表头开始到入环第一个结点的距离是相同的,因此,meet 和 cur 一定会相遇
