当前位置：首页 > news >正文

从图卷积网络（GCN）到简化图卷积网络（SGC）的对话

news 2025/8/29 6:29:43

此文是模仿导师教导学生对话式的论文阅读笔记
适用于对GNN有了解，但是人工智能，图论基础都不太好的学生

《Simplifying Graph Convolutional Networks》
SGC：简化图卷积网络
论文地址：https

- - **第一讲：GCN 的本质——从深度学习到图**
  - - **GCN 的伪代码：**
  - **第二讲：GCN 的核心难题**
  - **第三讲：SGC 的核心思想——单一线性化**
  - - **SGC 的伪代码：**
  - **第四讲：为何 SGC 能成功？**
  - **第五讲：SGC 与 GCN 的核心区别**
  - **第六讲：论文的实验评估与实际贡献**
  - **第七讲：对图神经网络领域的启示**

学生：
老师，您好！我这次的任务是深入理解图卷积网络（GCN）和一篇名为《Simplifying Graph Convolutional Networks》的简化图卷积的论文（SGC）。我虽然学过一些深度学习，但对图论和背后的理论基础感觉一头雾水，希望能得到您的细心指导。

老师：
下午好！没问题，我们来一起把这些概念理清楚。请不要有任何思想包袱，任何你觉得疑惑的地方都可以提出来。学习本身就是不断提问和解惑的过程。我们先从最基本的概念开始，一步步来。

第一讲：GCN 的本质——从深度学习到图

学生：
老师，我学过 MLP 和 CNN，这些模型都是在处理像图像和文本这样的规则数据，但 GCN 看起来很不一样。它到底是什么？

老师：
问得很好。GCN 的核心思想是把我们熟悉的卷积操作从规则数据（比如图像的网格像素）推广到不规则的图数据上。你可以这样理解：

CNN 的卷积核在一个局部小方框里滑动，对像素进行加权求和，目的是捕捉局部特征。
GCN 的“卷积”则是对一个节点的邻居进行加权求和，目的是聚合邻居的信息，从而捕捉图的局部结构。

简单来说，GCN 是一种能学习图上节点表示的神经网络。它通过堆叠多层，让每个节点不断地从它的邻居那里收集信息，从而学习到包含局部和全局结构信息的特征表示。

学生：
明白了。那 GCN 具体是怎么实现这种“邻居信息聚合”的呢？

老师：
这是一个关键问题。GCN 的每一层都包含三个核心步骤：特征传播、线性变换和非线性激活。

为了便于理解，我们用一个 K 层的 GCN 模型来做个简单的介绍。

GCN 的伪代码：

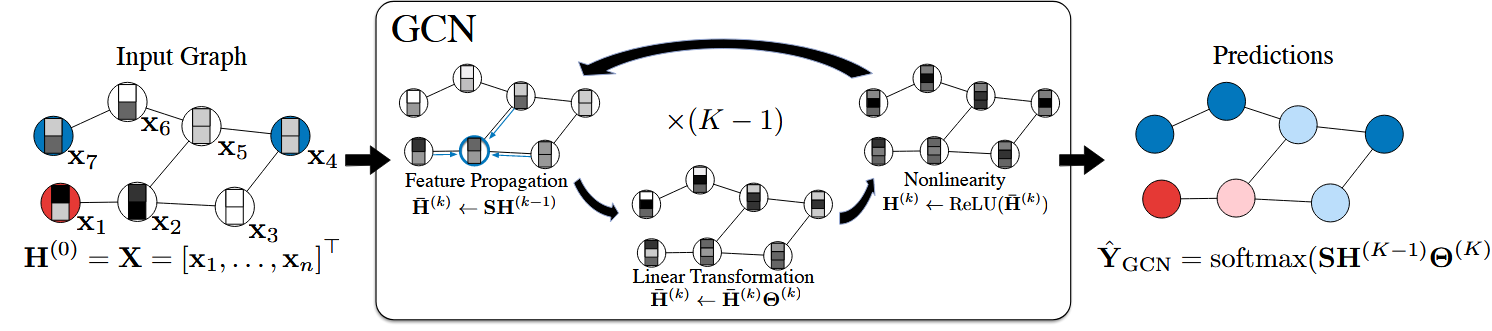
在这里插入图片描述

1. 输入准备

节点特征矩阵 X：包含了所有节点的特征，假设有 n 个节点，每个节点有 d 个特征，那么 X 的维度就是 $\times d$ 。
标准化邻接矩阵 S：这个矩阵是图结构信息的体现，它决定了每个节点从邻居那里聚合信息的权重。我们稍后会详细讲它。通常 $\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$ ，其中 $A~=A+I\tilde{A} = A + I$ （ $A$ 是邻接矩阵， $I$ 是单位矩阵）， $D~\tilde{D}$ 是 $A~\tilde{A}$ 的度矩阵。
K 个权重矩阵 $Θ(1),Θ(2),...,Θ(K)\Theta^{(1)}, \Theta^{(2)}, ..., \Theta^{(K)}$ ：这是模型需要学习的参数，用于进行线性变换。

2. 初始化

我们将初始的节点特征矩阵 X 设为 GCN 第一层的输入，记作 $H^{(0)} = X$ 。

3. 逐层传播

对于 k = 1 到 K：
- 特征传播（Feature Propagation）： 这一步实现了邻居信息的聚合。
  - $H‾(k)←SH(k−1)\overline{H}^{(k)} \leftarrow S H^{(k-1)}$
  - 这一步通过矩阵乘法，将上一层的节点表示 $H^{(k-1)}$ 与标准化邻接矩阵 $S$ 相乘。这就像是每个节点都按照 $S$ 中定义的权重，将邻居的特征加权平均到自己的特征中。
- 线性变换（Linear Transformation）： 这一步将聚合后的特征进行组合。
  - $H~(k)←H‾(k)Θ(k)\tilde{H}^{(k)} \leftarrow \overline{H}^{(k)} \Theta^{(k)}$
  - 模型学习一个权重矩阵 $Θ(k)\Theta^{(k)}$ ，将聚合后的特征 $H‾(k)\overline{H}^{(k)}$ 进行线性变换，生成新的特征表示。
- 非线性激活（Nonlinear Activation）： 这一步引入非线性，增加模型表达能力。
  - $H(k)←ReLU(H~(k))H^{(k)} \leftarrow \text{ReLU}(\tilde{H}^{(k)})$
  - 对线性变换的结果应用一个非线性函数，如 ReLU，以打破线性模型的局限，让模型能够学习更复杂的模式。

4. 最终预测

经过 K 层传播后，我们得到最终的节点表示 $H^{(K)}$ 。
在最后一层，我们通常会用一个 softmax 分类器来对节点进行分类：
- $Y^GCN=softmax(SH(K−1)Θ(K))\hat{Y}_{GCN} = \text{softmax}(S H^{(K-1)} \Theta^{(K)})$ (或者 $Y^GCN=softmax(H(K))\hat{Y}_{GCN} = \text{softmax}(H^{(K)})$ ，取决于具体实现)

这个过程就像是在一个多层神经网络的基础上，每一步都先让节点信息和它的邻居“交流”一下。你对此有初步的理解了吗？

第二讲：GCN 的核心难题

学生：
老师，听您这么一说，我感觉 GCN 的逻辑很清晰，就是不断地聚合、变换、激活。那为什么这篇论文还要“简化”它呢？是不是 GCN 有什么问题？

老师：
问得好！任何模型都不是完美的，GCN 也一样。尽管它在很多任务上表现出色，但它也继承了深度学习的一些“包袱”，这正是这篇论文想要解决的问题。

你可以想象一下，GCN 就像一个特别复杂的机器。它有很多层，每一层都有一套学习参数和非线性激活。这带来了几个潜在的问题：

不必要的复杂性： 在深度学习的历史上，通常是从简单的线性模型（如感知机）开始，当它们无法解决复杂问题时，才逐渐引入非线性和多层结构。然而，GCN 诞生于“神经网络复兴”之后，它从一开始就构建在多层网络之上，可能继承了对某些任务而言并不必要的复杂性。
冗余计算： 每一层都需要进行特征传播、线性变换和非线性激活，这会带来大量的计算开销，尤其是在处理大型图时，内存消耗也会非常大。这篇论文的作者们提到，在 Reddit 这样的超大规模数据集上，GCN 因为内存占用过高而无法训练。
可解释性差： 随着层数的增加和非线性的引入，GCN 的工作机制变得越来越像一个“黑箱”。我们很难直观地理解每一层到底在做什么，以及模型的预测是基于哪些特征。

这篇论文的作者们正是基于这些观察，提出了一个大胆的假设：
GCN 的强大能力，可能主要来源于它的特征传播，而层间的非线性激活函数并非总是必需的。 他们想要证明，即使去除了这些复杂性，模型依然可以保持出色的性能。

学生： 原来如此！那他们是怎么移除这些复杂性的呢？

老师： 他们做了一个非常直接且大胆的尝试，我称之为“单一线性化”。

第三讲：SGC 的核心思想——单一线性化

学生：
老师，这个“线性化”具体是怎么做的？

老师：
SGC 的核心思路是，移除 GCN 层间的所有非线性激活函数，并将所有线性变换合并成一个单一的线性变换。

我们来回顾一下 GCN 的传播规则：
$H(k)←ReLU(SH(k−1)Θ(k))H^{(k)} \leftarrow \text{ReLU}(S H^{(k-1)} \Theta^{(k)})$

现在，我们把非线性激活函数 ReLU 去掉，并把所有层的权重矩阵合并起来。假设一个 K 层的 GCN，它会变成这样：
$Y^←softmax(S(...(S(SXΘ(1))Θ(2))...)Θ(K))\hat{Y} \leftarrow \text{softmax}(S(...(S(S X \Theta^{(1)}) \Theta^{(2)})...) \Theta^{(K)})$

这个公式看起来很复杂，但由于所有操作都是线性的（矩阵乘法），我们可以对它进行简化。根据矩阵乘法的结合律，我们可以将所有 $S$ 矩阵和所有 $Θ\Theta$ 矩阵分别合并。

SGC 的伪代码：

在这里插入图片描述

1. 特征预处理

合并传播矩阵： 将 K 次传播操作合并为一步。
- $Xˉ←SKX\bar{X} \leftarrow S^K X$
- 这里的 $S^K$ 表示将标准化邻接矩阵 $S$ 自乘 $K$ 次，邻接矩阵 $S$ 的和GNC的一样。这一步是固定的，不需要学习任何参数。
此时，重归一化技巧并没有作为一个单独的步骤出现在伪代码中，因为它是一个预处理步骤，是在构建模型之前就已经完成的。伪代码中的 S 矩阵，从一开始就已经是一个经过重归一化处理的矩阵了。正是这个隐藏在输入中的 S 矩阵是一个固定的、没有可学习参数的矩阵，使得 $S^K$ 可以在多次传播后保持稳定，从而让 SGC 模型能够有效运作。

2. 训练分类器

合并权重矩阵： 将所有层的权重矩阵合并为一个。
- $Θ←Θ(1)Θ(2)...Θ(K)\Theta \leftarrow \Theta^{(1)} \Theta^{(2)} ... \Theta^{(K)}$
训练模型： SGC 最终的预测可以写成一个极其简单的公式。
- $Y^SGC=softmax(XˉΘ)=softmax(SKXΘ)\hat{Y}_{SGC} = \text{softmax}(\bar{X} \Theta) = \text{softmax}(S^K X \Theta)$
- 这一步等价于在一个预先处理好的特征矩阵 $Xˉ\bar{X}$ 上，训练一个标准的多类别逻辑回归分类器。

学生：
哇，真的太简单了！那它还能像 GCN 一样工作吗？

老师：
这正是这篇论文最令人惊讶的地方。作者们在实验中发现，SGC 在许多任务上的性能与 GCN 旗鼓相当，甚至在某些情况下表现得更好。

这个结果告诉我们，GCN 的强大之处，很可能主要源于其 K 步的特征传播（ $S^K X$ ），而不是层间的非线性变换。而 SGC 正是保留了这一点，同时去除了不必要的复杂性，从而在效率上实现了质的飞跃。

你对 SGC 的逻辑理解得怎么样了？接下来我们来深入探讨这篇论文最有价值的部分之一：从理论和实践两个角度，解释 SGC 为什么能成功，以及它和 GCN 的核心区别。

第四讲：为何 SGC 能成功？

学生：
老师，我还是有点不敢相信，去掉那么多层，只用一步就能得到好结果？这背后有什么理论支持吗？

老师：
这是一个非常好的疑问。SGC 的成功并非偶然，而是基于对 GCN 核心机制的深刻洞察。这篇论文从谱域分析的角度，为 SGC 提供了坚实的理论基础。

你还记得我们之前用过的比喻吗？把图上的节点特征看作是信号，GCN 的传播操作就是在平滑这些信号。这篇论文从数学上证明了这一点。

1. SGC 作为固定低通滤波器

图信号的“频率”： 在图谱理论中，图的拉普拉斯矩阵的特征值可以被视为图上信号的“频率”。小的特征值对应低频信号，大的特征值对应高频信号。
低频信号的意义： 在图上，低频信号代表的是平滑的特征。也就是说，如果一个信号是低频的，那么相邻节点的特征值就会非常相似。
SGC 的作用： 这篇论文证明，SGC 的核心操作 $Xˉ=SKX\bar{X} = S^K X$ 相当于一个固定参数的低通滤波器。它允许低频信号通过，同时抑制高频信号。这使得经过 K 步传播后，节点的特征变得更加平滑，连接紧密的节点会获得相似的表示。

2. “重归一化技巧”的深层意义

学生： 我记得您之前提过 GCN 论文中有一个“重归一化技巧”（Renormalization Trick），它好像很重要？
老师： 非常敏锐！这个技巧（在邻接矩阵中添加自环 $A~=A+I\tilde{A} = A + I$ ）是 GCN 和 SGC 能够成功的关键之一。从理论上讲，它有效地缩小了图谱的范围，也就是降低了最大特征值。
学生： 缩小图谱有什么好处呢？
老师： 这是一个关键点。当图谱范围变小时，SGC 的传播操作 $S^K$ 就能够更稳定地充当一个低通滤波器。如果没有这个技巧，高次幂的 $S$ 矩阵可能会导致某些频率的信号被过度放大或扭曲，从而使得模型性能随着 K 的增加而下降。这篇论文的实验结果也证实了这一点：加了自环（Aug. Normalized Adj.）的模型性能更稳定，而不加自环（Normalized Adj.）的模型，在奇数次方（如 K=3, 5）时性能会急剧下降。

所以，SGC 的成功，可以归结为两点：

它保留了最重要的机制：即通过多步传播实现的特征平滑。
它利用了“重归一化技巧”：确保了这种平滑操作能够稳定有效地进行。

第五讲：SGC 与 GCN 的核心区别

学生：
我觉得我已经理解 SGC 的理论了，但是它和 GCN 到底有什么本质区别呢？它们不都是在做特征聚合吗？

老师：
你的问题非常核心。从宏观上看，它们都在做特征聚合，但它们的实现方式和哲学思想截然不同。

我们可以从三个角度来对比：

1. 模型结构

GCN： 是一个多层、端到端的深度学习模型，包含了多层的线性变换和非线性激活。
SGC： 是一个单层、解耦的模型。它将特征提取（多步传播）和分类（逻辑回归）分成了两个独立的步骤。

2. 核心机制

GCN： 认为特征聚合和非线性变换同等重要，通过层层堆叠来学习复杂的特征层次。
SGC： 认为特征聚合（通过 $S^K$ 实现的特征平滑）才是 GCN 的主要效用来源。非线性变换的作用在很多任务上可能并不关键。

3. 效率与可解释性

GCN： 由于多层非线性结构，模型参数多，计算量大，尤其在处理大规模图时容易遇到内存问题。其“黑箱”特性也使得可解释性较差。
SGC： 由于将特征预处理和分类解耦，训练时只需要学习一个简单的权重矩阵，参数少，计算量极低。这使得它在 Reddit 等大型数据集上比其他模型快很多。同时，它可解释性很强，因为它本质上就是一个在平滑特征上的逻辑回归。

这篇论文的结论是，SGC 应该被视为 GCN 的一个重要基准（baseline）。当面对一个图任务时，我们应该先尝试像 SGC 这样简单的模型，如果它的性能足够好，就没有必要使用复杂的 GCN。只有在简单的模型不足以解决问题时，才应该考虑增加非线性或其他复杂性。

现在，你觉得对 GCN 和 SGC 的异同有了更清晰的认识吗？

第六讲：论文的实验评估与实际贡献

学生：
老师，这篇论文除了理论上说得通，它在实验上真的证明了SGC比GCN更好吗？

老师：
这是一个关键问题。论文的作者们通过大量实验，非常有力地证明了SGC在许多方面与GCN相当甚至更优。他们主要通过以下几点来展示SGC的优势：

性能上的竞争力：
- 在引文网络（如Cora、Citeseer、Pubmed）的节点分类任务上，SGC的准确率与GCN和其他一些最先进的图神经网络（如GAT）相当。
- 特别是在Citeseer数据集上，SGC的性能甚至比GCN高出约1%。作者们推测，这可能是因为SGC参数更少，不容易过拟合。
- 在大型社交网络Reddit上，SGC的表现也超过了其他基于采样的GCN变体（如SAGE-GCN和FastGCN）。
效率上的巨大优势：
- 这是SGC最引人注目的优点。通过将特征传播预处理为一步 $Xˉ=SKX\bar{X} = S^K X$ ，SGC的训练时间大大减少。
- 在Pubmed数据集上，SGC比GCN快了大约28倍。
- 在最大的Reddit数据集上，SGC的训练速度甚至比基于采样的FastGCN快了两个数量级。
- SGC的内存占用也小得多，解决了GCN在大型图上可能出现的“内存不足”问题。
对下游任务的泛化能力：
- 论文还展示了SGC在其他多个应用领域的有效性，包括文本分类、用户地理定位、关系抽取和零样本图像分类。
- 例如，在文本分类任务中，SGC的性能与GCN相当，但速度快了很多倍。这证明了SGC的简化思想并不仅限于节点分类，在不同类型的图学习任务中也同样适用。

第七讲：对图神经网络领域的启示

学生：
老师，既然SGC这么好，它对整个图神经网络领域有什么影响呢？

老师：
SGC的成功不仅仅在于提供了一个更快的模型，它的核心贡献在于对图神经网络的重新审视。

一个强大的基准：
- SGC的论文提出，SGC应该成为未来图学习模型的一个强大而简单的基准（baseline）。
- 任何新的、复杂的图神经网络模型，都应该首先与SGC进行比较。如果一个复杂的模型无法显著优于SGC，那么它的额外复杂性可能是不必要的。
鼓励“由简入繁”的研究路径：
- 这篇论文鼓励研究者们回归到机器学习的历史传统，即先从一个简单、可解释的模型开始，只有在简单的模型不足时，再逐步增加复杂性。
- SGC证明，图传播是图神经网络的核心，非线性、多层等复杂性是建立在这个核心之上的。这为未来的研究提供了一个明确的方向：可以先专注于改进特征传播机制，然后再考虑其他高级功能。
提供了一种可解释的视角：
- 通过将模型解耦为固定特征提取和简单分类器，SGC极大地增强了可解释性。
- 我们可以直观地理解，SGC的预测是基于平滑后的节点特征，这使得我们能够更好地理解模型是如何利用图结构做出决策的。
探索更多相关工作
这篇论文的出现激发了图神经网络领域的许多新思路，比如如何设计更简单、更高效的模型。你可以查阅一些相关的后续工作，比如：
- APPNP (Predict then Propagate): 这篇论文也提出了一种将非线性变换和特征传播分离的思路，与 SGC 有异曲同工之妙。
- MixHop: 这篇论文则探索了在不同传播步数上对特征进行聚合，这与 SGC 的 SK 思想有所关联。