当前位置：首页 > news >正文

【深度学习-Day 44】GRU详解：LSTM的优雅继任者？门控循环单元原理与PyTorch实战

news 2025/8/28 12:13:29

Langchain系列文章目录

01-玩转LangChain：从模型调用到Prompt模板与输出解析的完整指南
02-玩转 LangChain Memory 模块：四种记忆类型详解及应用场景全覆盖
03-全面掌握 LangChain：从核心链条构建到动态任务分配的实战指南
04-玩转 LangChain：从文档加载到高效问答系统构建的全程实战
05-玩转 LangChain：深度评估问答系统的三种高效方法（示例生成、手动评估与LLM辅助评估）
06-从 0 到 1 掌握 LangChain Agents：自定义工具 + LLM 打造智能工作流！
07-【深度解析】从GPT-1到GPT-4：ChatGPT背后的核心原理全揭秘
08-【万字长文】MCP深度解析：打通AI与世界的“USB-C”，模型上下文协议原理、实践与未来

Python系列文章目录

PyTorch系列文章目录

机器学习系列文章目录

深度学习系列文章目录

Java系列文章目录

JavaScript系列文章目录

深度学习系列文章目录

01-【深度学习-Day 1】为什么深度学习是未来？一探究竟AI、ML、DL关系与应用
02-【深度学习-Day 2】图解线性代数：从标量到张量，理解深度学习的数据表示与运算
03-【深度学习-Day 3】搞懂微积分关键：导数、偏导数、链式法则与梯度详解
04-【深度学习-Day 4】掌握深度学习的“概率”视角：基础概念与应用解析
05-【深度学习-Day 5】Python 快速入门：深度学习的“瑞士军刀”实战指南
06-【深度学习-Day 6】掌握 NumPy：ndarray 创建、索引、运算与性能优化指南
07-【深度学习-Day 7】精通Pandas：从Series、DataFrame入门到数据清洗实战
08-【深度学习-Day 8】让数据说话：Python 可视化双雄 Matplotlib 与 Seaborn 教程
09-【深度学习-Day 9】机器学习核心概念入门：监督、无监督与强化学习全解析
10-【深度学习-Day 10】机器学习基石：从零入门线性回归与逻辑回归
11-【深度学习-Day 11】Scikit-learn实战：手把手教你完成鸢尾花分类项目
12-【深度学习-Day 12】从零认识神经网络：感知器原理、实现与局限性深度剖析
13-【深度学习-Day 13】激活函数选型指南：一文搞懂Sigmoid、Tanh、ReLU、Softmax的核心原理与应用场景
14-【深度学习-Day 14】从零搭建你的第一个神经网络：多层感知器(MLP)详解
15-【深度学习-Day 15】告别“盲猜”：一文读懂深度学习损失函数
16-【深度学习-Day 16】梯度下降法 - 如何让模型自动变聪明？
17-【深度学习-Day 17】神经网络的心脏：反向传播算法全解析
18-【深度学习-Day 18】从SGD到Adam：深度学习优化器进阶指南与实战选择
19-【深度学习-Day 19】入门必读：全面解析 TensorFlow 与 PyTorch 的核心差异与选择指南
20-【深度学习-Day 20】PyTorch入门：核心数据结构张量(Tensor)详解与操作
21-【深度学习-Day 21】框架入门：神经网络模型构建核心指南 (Keras & PyTorch)
22-【深度学习-Day 22】框架入门：告别数据瓶颈 - 掌握PyTorch Dataset、DataLoader与TensorFlow tf.data实战
23-【深度学习-Day 23】框架实战：模型训练与评估核心环节详解 (MNIST实战)
24-【深度学习-Day 24】过拟合与欠拟合：深入解析模型泛化能力的核心挑战
25-【深度学习-Day 25】告别过拟合：深入解析 L1 与 L2 正则化（权重衰减）的原理与实战
26-【深度学习-Day 26】正则化神器 Dropout：随机失活，模型泛化的“保险丝”
27-【深度学习-Day 27】模型调优利器：掌握早停、数据增强与批量归一化
28-【深度学习-Day 28】告别玄学调参：一文搞懂网格搜索、随机搜索与自动化超参数优化
29-【深度学习-Day 29】PyTorch模型持久化指南：从保存到部署的第一步
30-【深度学习-Day 30】从MLP的瓶颈到CNN的诞生：卷积神经网络的核心思想解析
31-【深度学习-Day 31】CNN基石：彻底搞懂卷积层 (Convolutional Layer) 的工作原理
32-【深度学习-Day 32】CNN核心组件之池化层：解密最大池化与平均池化
33-【深度学习-Day 33】从零到一：亲手构建你的第一个卷积神经网络（CNN）
34-【深度学习-Day 34】CNN实战：从零构建CIFAR-10图像分类器（PyTorch）
35-【深度学习-Day 35】实战图像数据增强：用PyTorch和TensorFlow扩充你的数据集
36-【深度学习-Day 36】CNN的开山鼻祖：从LeNet-5到AlexNet的架构演进之路
37-【深度学习-Day 37】VGG与GoogLeNet：当深度遇见宽度，CNN架构的演进之路
38-【深度学习-Day 38】破解深度网络退化之谜：残差网络（ResNet）核心原理与实战
39-【深度学习-Day 39】玩转迁移学习与模型微调：站在巨人的肩膀上
40-【深度学习-Day 40】RNN入门：当神经网络拥有记忆，如何处理文本与时间序列？
41-【深度学习-Day 41】解密循环神经网络（RNN）：深入理解隐藏状态、参数共享与前向传播
42-【深度学习-Day 42】RNN的“记忆”难题：深入解析长期依赖与梯度消失/爆炸
43-【深度学习-Day 43】解密LSTM：深入理解长短期记忆网络如何克服RNN的遗忘症
44-【深度学习-Day 44】GRU详解：LSTM的优雅继任者？门控循环单元原理与PyTorch实战

文章目录

Langchain系列文章目录
Python系列文章目录
PyTorch系列文章目录
机器学习系列文章目录
深度学习系列文章目录
Java系列文章目录
JavaScript系列文章目录
深度学习系列文章目录
摘要
一、回顾：LSTM的强大与复杂
- 1.1 LSTM的核心贡献：门控机制
- 1.2 复杂性带来的挑战
二、GRU（门控循环单元）登场
- 2.1 GRU的核心思想：简化与融合
- 2.2 GRU的两大门：更新门与重置门
- - 2.2.1 重置门 (Reset Gate, $r_t$ )
  - 2.2.2 更新门 (Update Gate, $z_t$ )
三、GRU的内部工作流程
- 3.1 候选隐藏状态的计算 ( $h~t\tilde{h}_t$ )
- 3.2 最终隐藏状态的更新 ( $h_t$ )
- 3.3 可视化图解
四、GRU vs LSTM：一场优雅的对决
- 4.1 结构与参数对比
- 4.2 性能与收敛
- 4.3 何时选择GRU？何时选择LSTM？
- - - （1）优先考虑 GRU 的场景
    - （2）优先考虑 LSTM 的场景
五、PyTorch实战：使用GRU层
- 5.1 `nn.GRU` 核心参数解析
- 5.2 构建一个简单的GRU模型
- 5.3 模拟输入与前向传播
六、总结

摘要

在深度学习处理序列数据的领域，LSTM（长短期记忆网络）以其强大的门控机制解决了传统 RNN 的长期依赖问题，一度成为王者。然而，其复杂的结构和较高的计算成本也促使研究者探索更高效的替代方案。本文将深入探讨 LSTM 的一个重要变体——GRU（Gated Recurrent Unit，门控循环单元）。我们将从 GRU 的核心思想出发，详细拆解其内部的更新门与重置门，并通过图解和公式清晰展示其工作流程。此外，本文还将对 GRU 和 LSTM 进行全方位对比，分析它们各自的优劣与适用场景，帮助你做出明智的模型选择。最后，我们将通过 PyTorch 代码实战，带你亲手构建和使用 GRU 模型，将理论知识转化为实践能力。

一、回顾：LSTM的强大与复杂

在正式进入 GRU 的世界之前，让我们先简要回顾一下它的前辈——LSTM，以便更好地理解 GRU 的设计动机。

1.1 LSTM的核心贡献：门控机制

我们在【深度学习-Day 43】中详细讨论过，LSTM 的革命性在于引入了门控机制（Gating Mechanism）和细胞状态（Cell State）。

细胞状态（Cell State, $C_t$ ）：像一条传送带，贯穿整个时间序列，负责长期记忆的传递。信息可以很容易地在上面流动而不发生大的改变。
三大门：
1. 遗忘门（Forget Gate）：决定从细胞状态中丢弃哪些旧信息。
2. 输入门（Input Gate）：决定让哪些新信息更新到细胞状态中。
3. 输出门（Output Gate）：决定从细胞状态中输出哪些信息作为当前时间步的隐藏状态。

这种精巧的设计使得 LSTM 能够有效地学习和记忆长期依赖关系，避免了梯度消失问题。

1.2 复杂性带来的挑战

尽管 LSTM 功能强大，但它的“豪华配置”也带来了一些挑战：

参数众多：三个门加上一个候选细胞状态的计算，涉及大量的权重矩阵和偏置项，导致模型参数较多。
计算成本高：更多的参数和更复杂的计算流程意味着在训练和推理时需要更多的计算资源和时间。
过拟合风险：在数据集规模不大时，复杂的模型更容易出现过拟合。

正是为了在保持 LSTM 核心优势的同时，简化模型、提高效率，GRU 应运而生。

二、GRU（门控循环单元）登场

GRU (Gated Recurrent Unit) 由 Cho 等人在 2014 年提出，是 LSTM 的一个非常流行和有效的变体。它巧妙地简化了 LSTM 的结构，却在许多任务上表现出旗鼓相当甚至更好的性能。

2.1 GRU的核心思想：简化与融合

GRU 的简化哲学体现在两个方面：

状态融合：GRU 将 LSTM 中的细胞状态（Cell State）和隐藏状态（Hidden State）合并为了一个单一的隐藏状态（ $h_t$ ）。这个隐藏状态同时承载了长期记忆和当前时间步输出的功能。
门控简化：GRU 将 LSTM 的三个门（遗忘门、输入门、输出门）减少到了两个：更新门（Update Gate）和重置门（Reset Gate）。

2.2 GRU的两大门：更新门与重置门

下面我们来详细解析 GRU 的两个核心组件。

2.2.1 重置门 (Reset Gate, $r_t$ )

功能：重置门决定了在计算当前候选隐藏状态时，需要多大程度上忽略掉前一个时间步的隐藏状态 $h_{t-1}$ 。它的作用是帮助模型捕捉序列中的短期依赖关系。
工作原理：重置门会查看前一个隐藏状态 $h_{t-1}$ 和当前输入 $x_t$ ，然后通过一个 Sigmoid 函数输出一个介于 0 和 1 之间的向量 $r_t$ 。
数学公式：
$rt=σ(Wr⋅[ht−1,xt]+br)r_t = \sigma(W_r \cdot [h_{t-1}, x_t] + b_r)$
- $x_t$ ：当前时间步的输入向量。
- $h_{t-1}$ ：前一时间步的隐藏状态。
- $h_{t-1}, x_t]$ ：表示将两个向量拼接起来。
- $W_r, b_r$ ：重置门的权重矩阵和偏置项，是模型需要学习的参数。
- $σ\sigma$ ：Sigmoid 激活函数，将输出值压缩到 $(0, 1)$ 范围内。
直观理解：如果 $r_t$ 的某个元素接近 0，意味着在计算新的候选记忆时，将完全“重置”或忽略掉前一状态对应维度的信息，让模型更关注当前输入 $x_t$ 。如果接近 1，则表示将前一状态的信息几乎全部保留。

2.2.2 更新门 (Update Gate, $z_t$ )

功能：更新门是 GRU 的“多面手”，它同时扮演了 LSTM 中遗忘门和输入门的角色。它决定了前一时间步的隐藏状态 $h_{t-1}$ 有多少信息需要被保留到当前隐藏状态 $h_t$ ，以及当前计算出的候选隐藏状态 $h~t\tilde{h}_t$ 有多少信息需要被添加进来。
工作原理：与重置门类似，更新门也接收 $h_{t-1}$ 和 $x_t$ 作为输入，通过 Sigmoid 函数输出一个向量 $z_t$ 。
数学公式：
$zt=σ(Wz⋅[ht−1,xt]+bz)z_t = \sigma(W_z \cdot [h_{t-1}, x_t] + b_z)$
- $W_z, b_z$ ：更新门的权重矩阵和偏置项，是模型需要学习的参数。
直观理解：更新门 $z_t$ 控制着信息的“流量”。如果 $z_t$ 的某个元素接近 1，意味着更多的新信息（来自候选状态）将被采纳。如果接近 0，则意味着更多地保留旧信息（来自前一状态）。这使得 GRU 能够有效地控制长期记忆的传递。

三、GRU的内部工作流程

了解了两个门之后，我们就可以将它们串联起来，看看 GRU 是如何在一个时间步内完成信息更新的。

3.1 候选隐藏状态的计算 ( $h~t\tilde{h}_t$ )

首先，模型需要计算一个“候选”的隐藏状态 $h~t\tilde{h}_t$ 。这个候选状态包含了当前输入 $x_t$ 的新信息，并有选择性地融入了过去的信息（由重置门 $r_t$ 控制）。

数学公式：
$h~t=tanh⁡(Wh⋅[rt⊙ht−1,xt]+bh)\tilde{h}_t = \tanh(W_h \cdot [r_t \odot h_{t-1}, x_t] + b_h)$
- $⊙\odot$ ：表示哈达玛积（Hadamard Product），即逐元素相乘。
- $rt⊙ht−1r_t \odot h_{t-1}$ ：这是关键步骤！重置门 $r_t$ 在这里发挥作用，它逐元素地乘以 $h_{t-1}$ 。如果 $r_t$ 的某个元素为 0，那么 $h_{t-1}$ 对应维度的信息就被“清零”，无法影响候选状态的计算。
- $W_h, b_h$ ：计算候选状态的权重矩阵和偏置项。
- $tanh⁡\tanh$ ：双曲正切函数，将输出值压缩到 $(- 1, 1)$ 范围内，作为候选的记忆内容。

3.2 最终隐藏状态的更新 ( $h_t$ )

最后一步，也是最精妙的一步，是利用更新门 $z_t$ 来平衡旧记忆 $h_{t-1}$ 和新记忆 $h~t\tilde{h}_t$ ，从而得到当前时间步最终的隐藏状态 $h_t$ 。

数学公式：
$ht=(1−zt)⊙ht−1+zt⊙h~th_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t$
- 这个公式是一个巧妙的线性插值。
- $z_t) \odot h_{t-1}$ ：这部分决定了要从前一状态 $h_{t-1}$ 中保留多少信息。如果 $z_t$ 接近 1，那么 $1 - z_t$ 就接近 0，意味着几乎不保留旧信息。
- $zt⊙h~tz_t \odot \tilde{h}_t$ ：这部分决定了要从候选状态 $h~t\tilde{h}_t$ 中采纳多少新信息。如果 $z_t$ 接近 1，意味着大量采纳新信息。
更新门 $z_t$ 就像一个开关，完美地平衡了“守旧”与“革新”，使得 GRU 能够灵活地更新其记忆。

3.3 可视化图解

为了更直观地理解 GRU 的工作流程，我们可以使用 Mermaid 语法绘制其内部结构图。

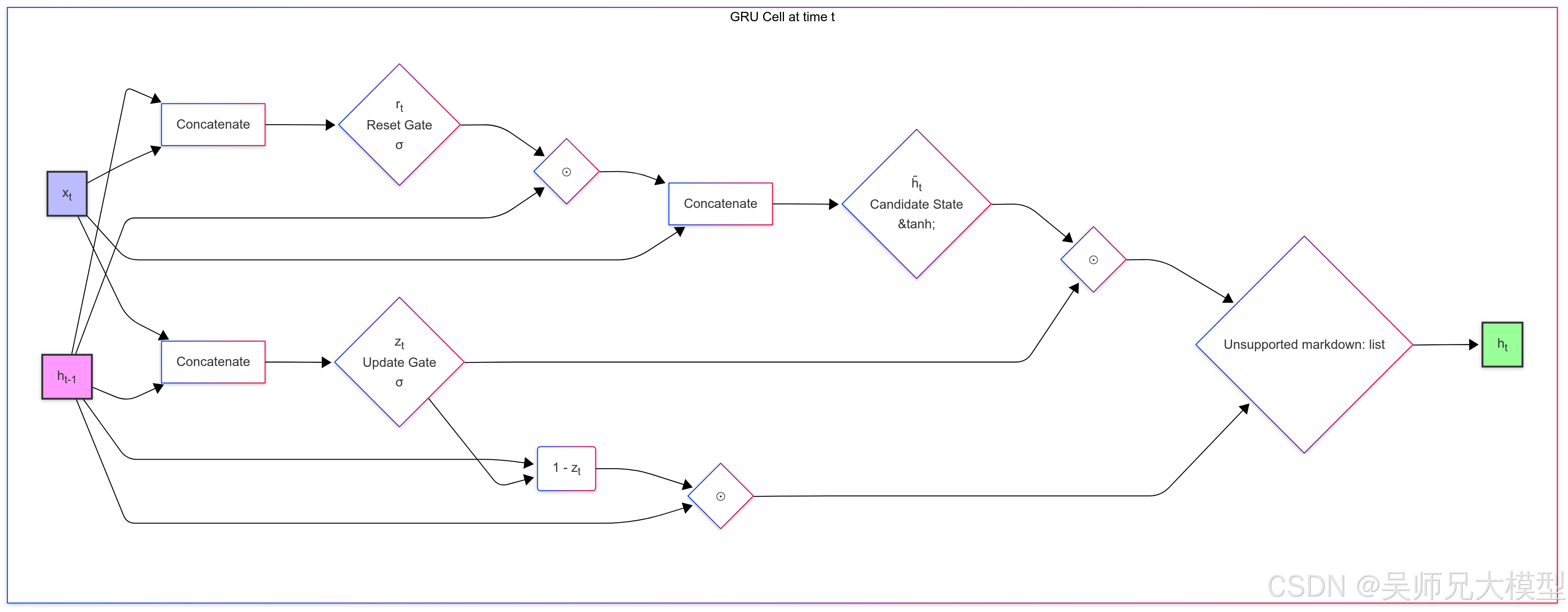
在这里插入图片描述

上图清晰地展示了输入 $x_t$ 和前一状态 $h_{t-1}$ 如何经过更新门和重置门的处理，最终生成新的隐藏状态 $h_t$ 。

四、GRU vs LSTM：一场优雅的对决

既然 GRU 是 LSTM 的变体，那么它们之间究竟有何异同？我们该如何选择？

4.1 结构与参数对比

特性	GRU (门控循环单元)	LSTM (长短期记忆网络)
核心状态	1个：隐藏状态 (Hidden State)	2个：细胞状态 (Cell State) 和隐藏状态 (Hidden State)
门控数量	2个：更新门、重置门	3个：遗忘门、输入门、输出门
参数量	较少	较多
计算效率	更高，训练速度通常更快	较低，训练速度通常更慢
设计哲学	简化、融合	精细、分工明确

4.2 性能与收敛

关于性能，学术界和工业界尚未有一致的结论表明谁绝对优于谁。通常情况如下：

性能相似：在许多任务上，经过仔细调优的 GRU 和 LSTM 模型可以达到非常相似的性能水平。
GRU的优势：由于参数更少，GRU 的训练速度更快。在数据量较小的情况下，更简单的结构可能有助于防止过拟合，从而获得更好的泛化能力。
LSTM的潜力：在处理需要捕捉极长依赖关系且数据极其复杂的任务时，LSTM 额外的细胞状态和更精细的门控分工可能使其具有更高的表达潜力，从而可能取得微弱的性能优势。

4.3 何时选择GRU？何时选择LSTM？

基于以上对比，我们可以总结出一些实用的选择策略：

（1）优先考虑 GRU 的场景

计算资源有限：如果你的 GPU 资源紧张或希望快速迭代模型，GRU 是一个绝佳的起点。
数据集规模中等或偏小：更少的参数意味着更低的过拟-合风险。
对训练速度要求高：GRU 的收敛速度通常更快。
作为基线模型：在项目初期，可以用 GRU 快速搭建一个基线模型，验证想法的可行性。

（2）优先考虑 LSTM 的场景

追求极致性能：如果你的计算资源充足，且任务对性能要求极高（例如，在学术竞赛或关键业务中），值得尝试 LSTM 并进行深度调优。
处理超长序列：当序列的依赖关系跨度非常大时，LSTM 独立的细胞状态可能提供了更强的记忆能力。
有大量现成研究可参考：LSTM 历史更悠久，有大量的论文和开源实现，遇到问题时更容易找到解决方案。

经验法则：从 GRU 开始尝试。 如果它的性能已经满足需求，那就没有必要换成更复杂的 LSTM。如果性能不佳，再考虑切换到 LSTM 或其他更复杂的模型架构。

五、PyTorch实战：使用GRU层

理论讲了这么多，让我们动手用 PyTorch 来实现一个 GRU 模型，感受它的简洁与强大。

5.1 `nn.GRU` 核心参数解析

PyTorch 提供了非常方便的 torch.nn.GRU 模块。其常用参数如下：

input_size：输入特征的维度。例如，对于词嵌入，它就是 embedding_dim。
hidden_size：隐藏状态的维度。这是 GRU 层的核心超参数。
num_layers：循环网络的层数。默认是 1。大于 1 表示构建一个堆叠（Stacked）GRU。
batch_first：一个极其重要的布尔值。如果为 True，则输入和输出张量的维度格式为 (batch_size, sequence_length, feature_dim)。这通常更符合直觉。默认为 False，格式为 (sequence_length, batch_size, feature_dim)。强烈建议始终设置为 True。
bidirectional：如果为 True，则构建一个双向 GRU。

5.2 构建一个简单的GRU模型

下面我们定义一个简单的、用于文本分类的 GRU 模型。它包含一个词嵌入层、一个 GRU 层和一个全连接输出层。

import torch
import torch.nn as nnclass GRUClassifier(nn.Module):def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, num_layers=1):"""初始化模型:param vocab_size: 词汇表大小:param embedding_dim: 词嵌入维度:param hidden_dim: GRU隐藏层维度:param output_dim: 输出维度 (例如，分类任务的类别数):param num_layers: GRU的层数"""super(GRUClassifier, self).__init__()# 1. 词嵌入层# 将输入的词索引转换为密集向量self.embedding = nn.Embedding(vocab_size, embedding_dim)# 2. GRU 层# batch_first=True 是一个好习惯，让输入维度更直观self.gru = nn.GRU(input_size=embedding_dim,hidden_size=hidden_dim,num_layers=num_layers,batch_first=True,bidirectional=False # 这里先使用单向GRU)# 3. 全连接输出层# 将GRU的最终隐藏状态映射到输出类别self.fc = nn.Linear(hidden_dim, output_dim)def forward(self, text):# text shape: [batch_size, seq_length]# 1. 通过嵌入层# embedded shape: [batch_size, seq_length, embedding_dim]embedded = self.embedding(text)# 2. 通过GRU层# gru_output shape: [batch_size, seq_length, hidden_dim]# hidden shape: [num_layers, batch_size, hidden_dim]gru_output, hidden = self.gru(embedded)# 3. 我们通常使用最后一个时间步的隐藏状态进行分类# hidden 是 [num_layers, batch_size, hidden_dim]，我们取最后一层# last_hidden shape: [batch_size, hidden_dim]last_hidden = hidden[-1, :, :]# 4. 通过全连接层得到最终输出# output shape: [batch_size, output_dim]output = self.fc(last_hidden)return output

5.3 模拟输入与前向传播

让我们创建模型的实例，并用一个模拟的输入数据来测试其前向传播过程。

# 定义模型超参数
VOCAB_SIZE = 1000  # 假设我们的词汇表有1000个词
EMBEDDING_DIM = 128
HIDDEN_DIM = 256
OUTPUT_DIM = 2     # 例如，二分类（正面/负面）
NUM_LAYERS = 2# 实例化模型
model = GRUClassifier(VOCAB_SIZE, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM, NUM_LAYERS)
print(model)# 创建模拟输入数据
BATCH_SIZE = 32
SEQ_LENGTH = 20
# 随机生成一个批次的文本数据（词索引）
dummy_input = torch.randint(0, VOCAB_SIZE, (BATCH_SIZE, SEQ_LENGTH))
print(f"\n输入张量形状: {dummy_input.shape}")# 前向传播
output = model(dummy_input)# 打印输出形状
print(f"输出张量形状: {output.shape}")# 检查输出形状是否符合预期
# 预期形状应为 [batch_size, output_dim]
assert output.shape == (BATCH_SIZE, OUTPUT_DIM)
print("\n模型前向传播成功，输出形状正确！")

代码输出示例：

GRUClassifier((embedding): Embedding(1000, 128)(gru): GRU(128, 256, num_layers=2, batch_first=True)(fc): Linear(in_features=256, out_features=2, bias=True)
)输入张量形状: torch.Size([32, 20])
输出张量形状: torch.Size([32, 2])模型前向传播成功，输出形状正确！

这段代码清晰地展示了如何用 PyTorch 构建一个 GRU 模型，并验证了数据在模型中流转的维度变化，证明了其可用性。

六、总结

本文对门控循环单元（GRU）进行了系统性的介绍，从核心原理到实战应用，希望能帮助你全面掌握这一重要的 RNN 变体。

核心思想：GRU 是 LSTM 的一个高效简化版，旨在用更少的参数和计算量解决长期依赖问题。
关键结构：GRU 抛弃了独立的细胞状态，将所有记忆功能整合到单一的隐藏状态中。它使用两个门——重置门（决定忽略多少过去信息）和更新门（决定如何组合新旧信息）——来控制信息流。
工作流程：GRU 通过重置门控制的候选状态计算，和更新门控制的最终状态线性插值，实现了对隐藏状态的灵活更新。
GRU vs. LSTM：两者在许多任务上性能相当。GRU 更快、参数更少，适合作为快速基线或在资源受限时使用。LSTM 结构更复杂，可能在处理极长、极复杂的序列时略有优势。
实践应用：在 PyTorch 等现代深度学习框架中，nn.GRU 提供了简单易用的接口，通过设置 batch_first=True 等参数，可以轻松地将其集成到各类序列建模任务中。