比赛竞猜算法设计思路
文章目录
- 总结
- 背景
- 分析
- 其它
- 动态赔率
- 庄家抽水
- 代码
总结
分三步走:
- 根据选手积分,估算选手两两之间的胜负概率
- 根据胜负概率矩阵,估算每个选手的夺冠概率
- 根据夺冠概率,制定每个选手的赔率
背景
在一场乒乓球赛事中,有N个人报名参加了比赛。
为了增添趣味性,想要给比赛增加一个竞猜环节。在比赛开始前,任何人都可以押注,赌某一个选手最终夺冠。如果猜对了,会有奖励,如果猜错了,赌注就打水漂了。
分析
一般思路是,系统给每个参赛选手设定一个赔率(odds)。比如,选手A的赔率是2,如果一个人X下注100元押A夺冠,则:
- 如果A夺冠,X得到赔付
100 * 2 = 200元,去除本金100元,净盈利是100元 - 如果A没有夺冠,则X损失100元
那么问题就转化为,庄家如何设置每个选手的赔率,才能兼顾公平与机会。
比如说,选手A是夺冠热门,那么:
- A的赔率不能太高,因为大家都认为A有较大概率夺冠,很容易在A身上集中过多的赌注,所以庄家要控制A的赔率不能太高
- 其它选手的赔率要高于A,越是冷门选手,赔率越要高一些,这样,才会提高大家押注冷门选手的积极性
- 总体的赔率要有所控制(不能过高或者过低),最好的情况是,无论谁夺冠,庄家都能在稳定的基础上,小赚一笔
为了简单起见,我们简化模型:
- 赔率不会动态变化
- 每个选手身上的押注金额和他的夺冠概率成正比
- 目标是公平赔率(后续可以在此基础上抽水)
先看最简单的情况,假设只有两个选手A和B参赛,他们水平相当,夺冠概率都是50%,则赔率显然应该都是2。这样,假设押A和押B的总赌注一样多,那么无论A夺冠还是B夺冠,最终都是平衡的。
对于更复杂的情况,有多名选手参赛,他们的水平有高有低,每个人的夺冠概率分别为 PA , PB , PC ,……,假设总押注金额为 M ,则选手A的押注金额是 M * PA ,选手B的押注金额是 M * PB ,以此类推。
在此基础上,每个选手的赔率为:
- A:
1 / PA - B:
1 / PB - C:
1 / PC - ……
证明:假设A夺冠,那么对于庄家而言,
- 总收入是
M - 总支出是
M * PA * (1 / PA) = M
庄家达成了收支平衡。
其他选手夺冠,也是一样的。
现在,问题转换为,如何估算每个选手夺冠的概率?
这里,我们可以使用Elo预期胜率公式。
对任意选手i和j,i战胜j的概率为:
P(i,j) = 1 / (1 + pow(10, (scorej−scorei)/k))
其中 k 是评分差缩放因子,表示敏感度,惯用值是400。 k 值越小,越敏感,也就是说高分选手有更大概率战胜低分选手。
比如,A的积分是1700,B的积分是1600,C的积分是1500,按上述公式:
- A战胜B(相差100分)的概率为:
1 / (1 + pow(10, (1600 - 1700) / 400)) = 0.64 - A战胜C(相差200分)的概率为:
1 / (1 + pow(10, (1500 - 1700) / 400)) = 0.76
如果觉得不太准确,可以适当调整k值,比如调整到200:
- A战胜B(相差100分)的概率为:
1 / (1 + pow(10, (1600 - 1700) / 200)) = 0.76 - A战胜C(相差200分)的概率为:
1 / (1 + pow(10, (1500 - 1700) / 200)) = 0.91
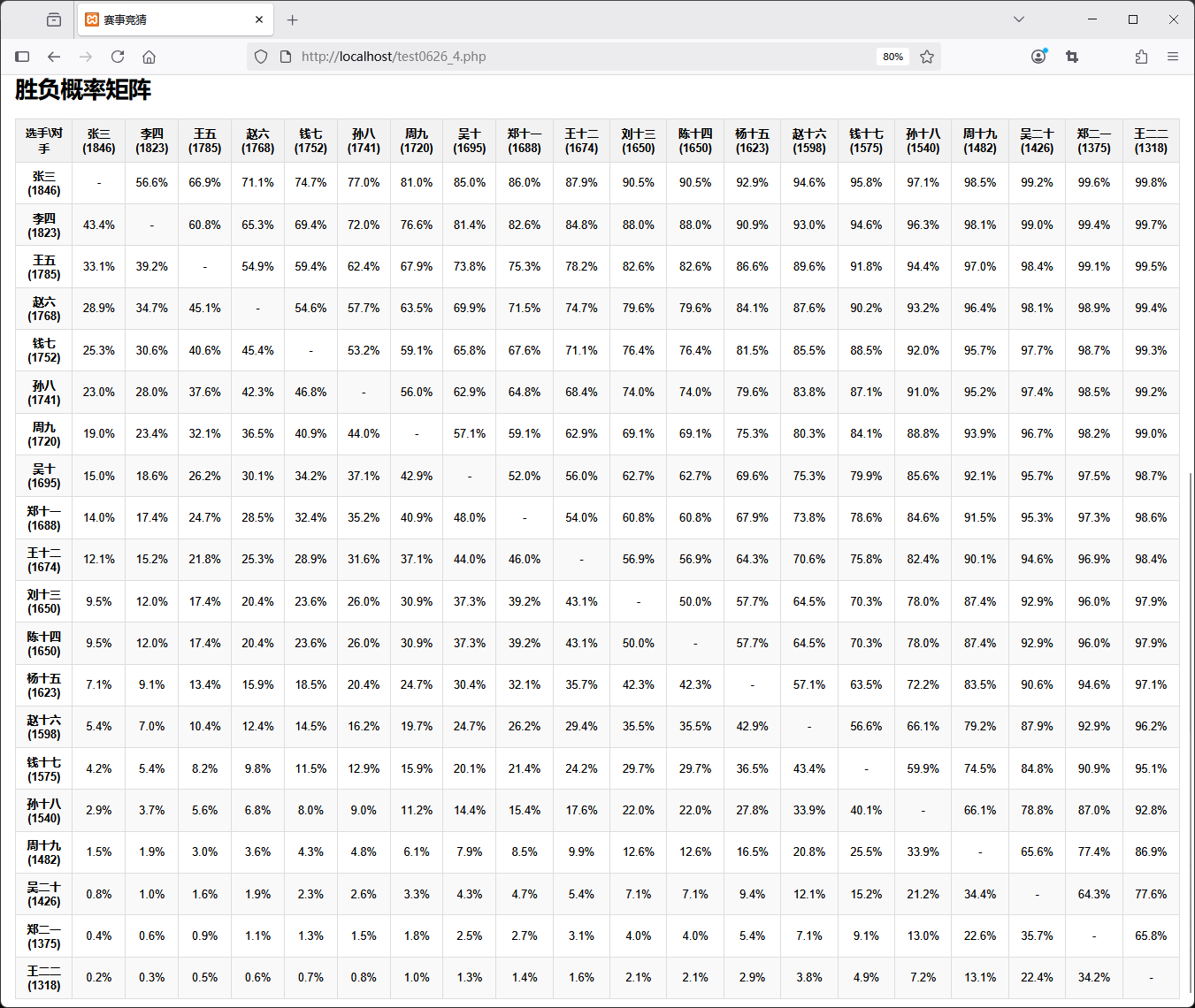
这样,根据每个选手的积分,我们可以得到一个胜负概率矩阵。
接下来,需要从胜负概率矩阵来估计每个选手的夺冠概率。
假设胜负概率矩阵如下:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | – | 0.7 | 0.8 | 0.9 | 0.95 |
| B | – | 0.7 | 0.8 | 0.9 | |
| C | – | 0.7 | 0.8 | ||
| D | – | 0.7 | |||
| E | – |
- A的预期胜场数:
0.7 + 0.8 + 0.9 + 0.95 = 3.35 - B的预期胜场数:
0.3 + 0.7 + 0.8 + 0.9 = 2.7 - C的预期胜场数:
0.2 + 0.3 + 0.7 + 0.8 = 2.0 - D的预期胜场数 :
0.1 + 0.2 + 0.3 + 0.7 = 1.3 - E的预期胜场数:
0.05 + 0.1 + 0.2 + 0.3 = 0.65
归一化:
3.35 + 2.7 + 2.0 + 1.3 + 0.65 = 10
PA = 3.35 / 10 = 33.5%PB = 2.7 / 10 = 27%PC = 2.0 / 10 = 20%PD = 1.3 / 10 = 13%PE = 0.65 / 10 = 6.5%
不过,这种算法貌似不太科学。强如A,有较大概率能战胜所有对手,而夺冠概率只有33.5%,而E基本上谁也赢不了,竟然还有6.5%的夺冠概率。
这说明胜负差异对夺冠概率的影响过小,显然,我们应该放大差异影响。
比如,使用平方加权法来代替线性归一法:
3.35^2 + 2.7^2 + 2.0^2 + 1.3^2 + 0.65^2 = 24.62
PA = 3.35^2 / 24.62 = 45.6%PB = 2.7^2 / 24.62 = 29.6%PC = 2.0^2 / 24.62 = 16.3%PD = 1.3^2 / 24.62 = 6.9%PE = 0.65^2 / 24.62 = 1.7%
这样一来,高分选手的夺冠概率趋向于更高,而低分选手的夺冠概率趋向于更低,更接近真实情况。
如果还想进一步放大差异,可以考虑三次方加权,估算结果如下:
- PA: 55.5%
- PB: 29.1%
- PC: 11.8%
- PD: 3.2%
- PE: 0.4%
看上去更合理一些。
其它
动态赔率
押注越高,赔率越低,避免出现庄家赔本的情况。本文没有考虑这种情况。
庄家抽水
比如在公平赔率基础上,打个九折,以保证庄家在稳定平衡基础上能小赚一笔。
代码
用PHP实现代码如下:
<?php
// $players = [
// ['uid' => 1, 'username' => '张三', 'score' => 2500],
// ['uid' => 2, 'username' => '李四', 'score' => 2200],
// ['uid' => 3, 'username' => '王五', 'score' => 2100],
// ['uid' => 4, 'username' => '赵六', 'score' => 2000],
// ['uid' => 5, 'username' => '钱七', 'score' => 1800],
// ];// $players = [
// ['uid' => 1, 'username' => '马龙', 'score' => 3200], // 超级王者
// ['uid' => 2, 'username' => '樊振东', 'score' => 3050], // 现役霸主
// ['uid' => 3, 'username' => '王楚钦', 'score' => 2900], // 新生代领军
// ['uid' => 4, 'username' => '许昕', 'score' => 2750], // 直板独苗
// ['uid' => 5, 'username' => '张继科', 'score' => 2750], // 同分选手1
// ['uid' => 6, 'username' => '林高远', 'score' => 2700],
// ['uid' => 7, 'username' => '梁靖崑', 'score' => 2600],
// ['uid' => 8, 'username' => '王皓', 'score' => 2550],
// ['uid' => 9, 'username' => '马琳', 'score' => 2450], // 传奇组
// ['uid' => 10, 'username' => '刘国梁', 'score' => 2450] // 同分选手2
// ];$players = [['uid' => 1, 'username' => '张三', 'score' => 1846],['uid' => 2, 'username' => '李四', 'score' => 1823], ['uid' => 3, 'username' => '王五', 'score' => 1785],['uid' => 4, 'username' => '赵六', 'score' => 1768],['uid' => 5, 'username' => '钱七', 'score' => 1752],['uid' => 6, 'username' => '孙八', 'score' => 1741],['uid' => 7, 'username' => '周九', 'score' => 1720],['uid' => 8, 'username' => '吴十', 'score' => 1695],['uid' => 9, 'username' => '郑十一', 'score' => 1688],['uid' => 10, 'username' => '王十二', 'score' => 1674],['uid' => 11, 'username' => '刘十三', 'score' => 1650],['uid' => 12, 'username' => '陈十四', 'score' => 1650], // 同分['uid' => 13, 'username' => '杨十五', 'score' => 1623],['uid' => 14, 'username' => '赵十六', 'score' => 1598],['uid' => 15, 'username' => '钱十七', 'score' => 1575],['uid' => 16, 'username' => '孙十八', 'score' => 1540],['uid' => 17, 'username' => '周十九', 'score' => 1482],['uid' => 18, 'username' => '吴二十', 'score' => 1426],['uid' => 19, 'username' => '郑二一', 'score' => 1375],['uid' => 20, 'username' => '王二二', 'score' => 1318]
];foreach ($players as &$player) {$totalExpectedWins = 0;foreach ($players as $opponent) {if ($player['uid'] == $opponent['uid']) continue;$winProbability = 1 / (1 + pow(10, - ($player['score'] - $opponent['score']) / 200));$totalExpectedWins += $winProbability;}$player['expectedWins'] = $totalExpectedWins;
}
unset($player);foreach ($players as &$player) {$player['expectedWins'] = pow($player['expectedWins'], 3);
}
unset($player);// 归一化处理
$total = 0;
foreach ($players as $player) {$total += $player['expectedWins'];
}foreach ($players as &$player) {$player['p'] = $player['expectedWins'] / $total;if ($player['p'] < 0.001) {$player['p'] = 0.001;}$player['odds_fair'] = number_format(1 / $player['p'], 2);$player['odds'] = number_format(1 / $player['p'] * 0.9, 2);if ($player['odds'] > 50) {$player['odds'] = 50;}
}
unset($player);?><!DOCTYPE html>
<html lang="zh-CN">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>赛事竞猜</title><style>body {font-family: Arial, sans-serif;margin: 20px;}table {width: 100%;border-collapse: collapse;margin-top: 20px;}th, td {border: 1px solid #ddd;padding: 8px;text-align: center;}th {background-color: #f2f2f2;font-weight: bold;}tr:nth-child(even) {background-color: #f9f9f9;}.probability {color: #2c7be5;}.odds {color: #d63200;font-weight: bold;}</style>
</head>
<body><h1>赔率表</h1><table><thead><tr><th>ID</th><th>比赛用名</th><th>积分</th><!-- <th>预计胜场</th> --><th>夺冠概率</th><th>公平赔率</th><th>赔率</th></tr></thead><tbody><?php foreach ($players as $player): ?><tr><td><?php echo $player['uid']; ?></td><td><?php echo $player['username']; ?></td><td><?php echo $player['score']; ?></td><!-- <td><?php echo $player['expectedWins']; ?></td> --><td class="probability"><?php echo $player['p'] * 100; ?>%</td><td class="odds"><?php echo $player['odds_fair']; ?></td><td class="odds"><?php echo $player['odds']; ?></td></tr><?php endforeach; ?></tbody></table><h1>胜负概率矩阵</h1><table><thead><tr><th>选手\对手</th><?php foreach ($players as $player): ?><th><?php echo $player['username'] . '('. $player['score']. ')'; ?></th><?php endforeach; ?></tr></thead><tbody><?php foreach ($players as $player1): ?><tr><td><strong><?php echo $player1['username'] . '('. $player1['score']. ')'; ?></strong></td><?php foreach ($players as $player2): ?><td><?php if ($player1['uid'] == $player2['uid']) {echo '-';} else {$prob = 1 / (1 + pow(10, - ($player1['score'] - $player2['score']) / 200));echo number_format($prob * 100, 1) . '%';}?></td><?php endforeach; ?></tr><?php endforeach; ?></tbody></table>
</body>
</html>
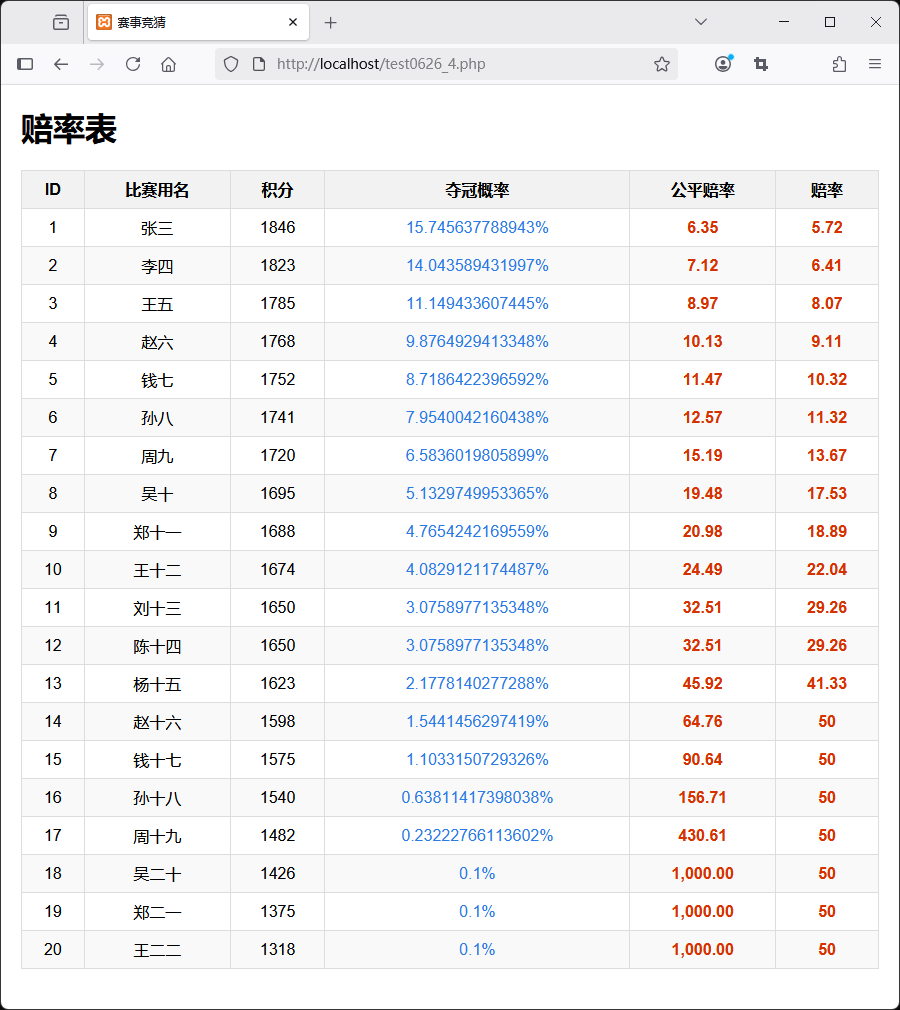
运行结果如下:
- 赔率表:
- 胜负概率矩阵: