吴恩达机器学习（一）

一、概述

机器学习定义：在没有明确设置的情况下，使计算机具有学习能力的研究领域。

特征：特征是描述样本的属性或变量，是模型用来学习和预测的基础。如：房屋面积、地理位置

标签：监督学习中需要预测的目标变量，是模型的输出目标。如：房屋价格

样本：如: {面积=100㎡,  位置=市中心, 价格=500万}, 数据集中的一个独立实例, 包含一组特征及对应的标签。

机器学习的分类：

①监督学习：利用带标签（正确答案）的数据训练模型，预测新样本的标签。如回归、分类。

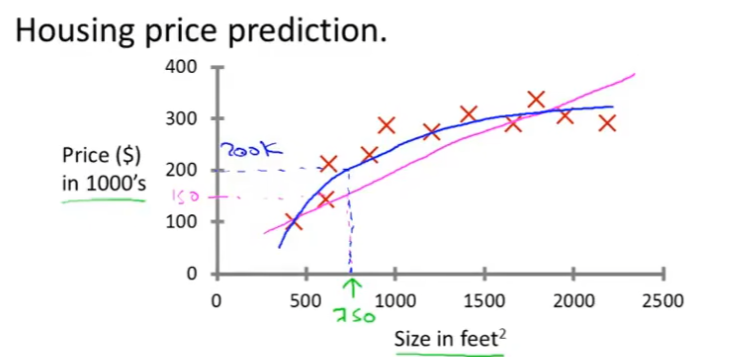
回归应用：房价预测

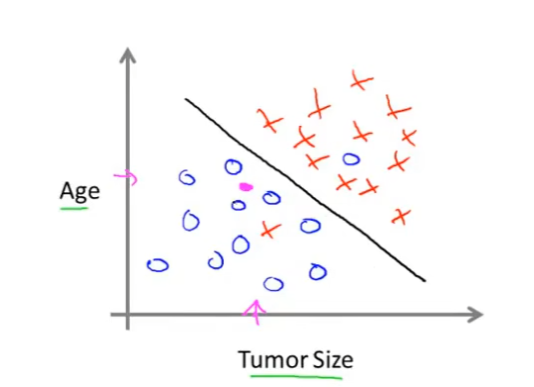
分类算法：根据年龄and肿瘤大小来判断肿瘤是良性还是恶性

②无监督学习：从未标注的数据集中发现潜在结构或模式，如聚类、异常检测、降维。

聚类算法：根据数据的相似度将数据分为多类的过程

降维算法：在保证数据所具有的代表性特征或分布的情况下，将高维数据转化为低维数据的过程，主要用于数据压缩和数据可视化。

二、模型

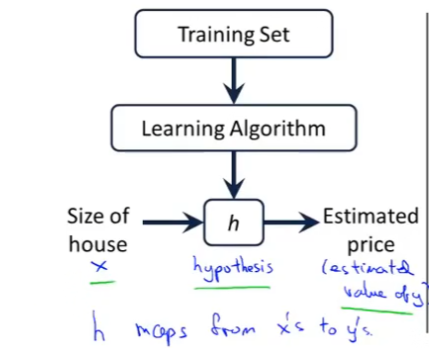
在一个训练数据集中，用m表示训练样本的数量；x表示输入变量（特征）；y表示输出变量（目标变量）。

学习算法的优化目标是用过选择参数来使得代价函数（Cost Function）最小。

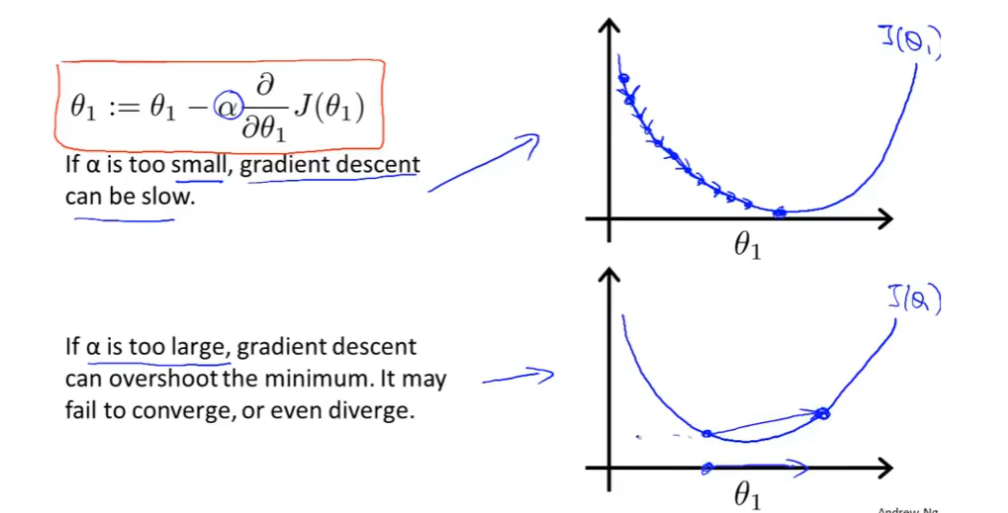
梯度下降（同步更新）：常见的优化算法，不仅用于线性回归而且广泛应用于机器学习的众多领域，是一种用于寻找最小化损失函数（或成本函数）的参数值。

梯度下降法在函数上起什么作用：找到导数的最小值

线性回归与梯度下降算法结合：

算法步骤：

① 初始化参数:随机初始化模型的参数（例如权重与偏置）

② 计算梯度：使用当前参数计算损失函数关于这些参数的梯度。梯度是一个向量，指示了损失函数在每个函数上的局部变化率。

③ 更新参数：根据梯度和学习率更新参数向量（负梯度方向），步长由学习率控制。学习率是一个超参数，决定了参数更新的幅度。

④ 重复迭代：重复步骤②和③，直到满足某个条件（例如达到最大迭代次数、损失函数值足够小或梯度足够小）。