当前位置：首页 > news >正文

动态规划：青蛙跳台阶

news 2025/8/28 9:43:30

一只青蛙要跳上有 n 级的台阶，每次只能跳 1 级或 2 级台阶，问青蛙总共有多少种不同的跳法？

加法原理

若完成一件事有多种 “互不重叠的路径”，则总方法数 = 各路径方法数之和。

在青蛙跳台阶问题中，加法原理的应用核心是 ——从 “最后一步的跳法” 倒推总跳法：
要跳到第 n 级台阶，青蛙的最后一步只有两种可能（因为每次只能跳 1 级或 2 级），且这两种可能完全独立、无重叠：

最后一步跳 1 级：说明青蛙在跳这 1 级之前，已经跳到了第 n-1 级台阶。此时，跳到第 n 级的方法数 = 跳到第 n-1 级的方法数（因为最后一步固定跳 1 级，不增加新的方法），即 f(n-1)；
最后一步跳 2 级：说明青蛙在跳这 2 级之前，已经跳到了第 n-2 级台阶。此时，跳到第 n 级的方法数 = 跳到第 n-2 级的方法数（最后一步固定跳 2 级），即 f(n-2)。

由于这两种路径覆盖了所有跳到第 n 级的可能（没有其他跳法），根据加法原理，总跳法数为两者之和：f(n) = f(n-1) + f(n-2)

跳到n-1层的跳法难道不会覆盖n-2层的跳法，难道不会有重合吗，怎么就是完全独立无重叠呢

集合划分保证无重叠

以 “最后一步的跳法” 划分集合

核心逻辑：无论前面怎么跳，最后一步只能是 “跳 1 级” 或 “跳 2 级”，因此总跳法 =“最后一步跳 1 级的方案数”+“最后一步跳 2 级的方案数”。

子集合 A（最后一步跳 1 级）：说明跳到第 5 级前，已先到第 4 级，对应 “跳到第 4 级的所有跳法”（共 f (4)=5 种）：

1->2->3->4->5（最后 1 级：4→5）
1->2->4->5（最后 1 级：4→5）
1->3->4->5（最后 1 级：4→5）
2->3->4->5（最后 1 级：4→5）
2->4->5（最后 1 级：4→5）

子集合 B（最后一步跳 2 级）：说明跳到第 5 级前，已先到第 3 级，对应 “跳到第 3 级的所有跳法”（共 f (3)=3 种）：

1->2->3->5（最后 2 级：3→5）
1->3->5（最后 2 级：3→5）
2->3->5（最后 2 级：3→5）

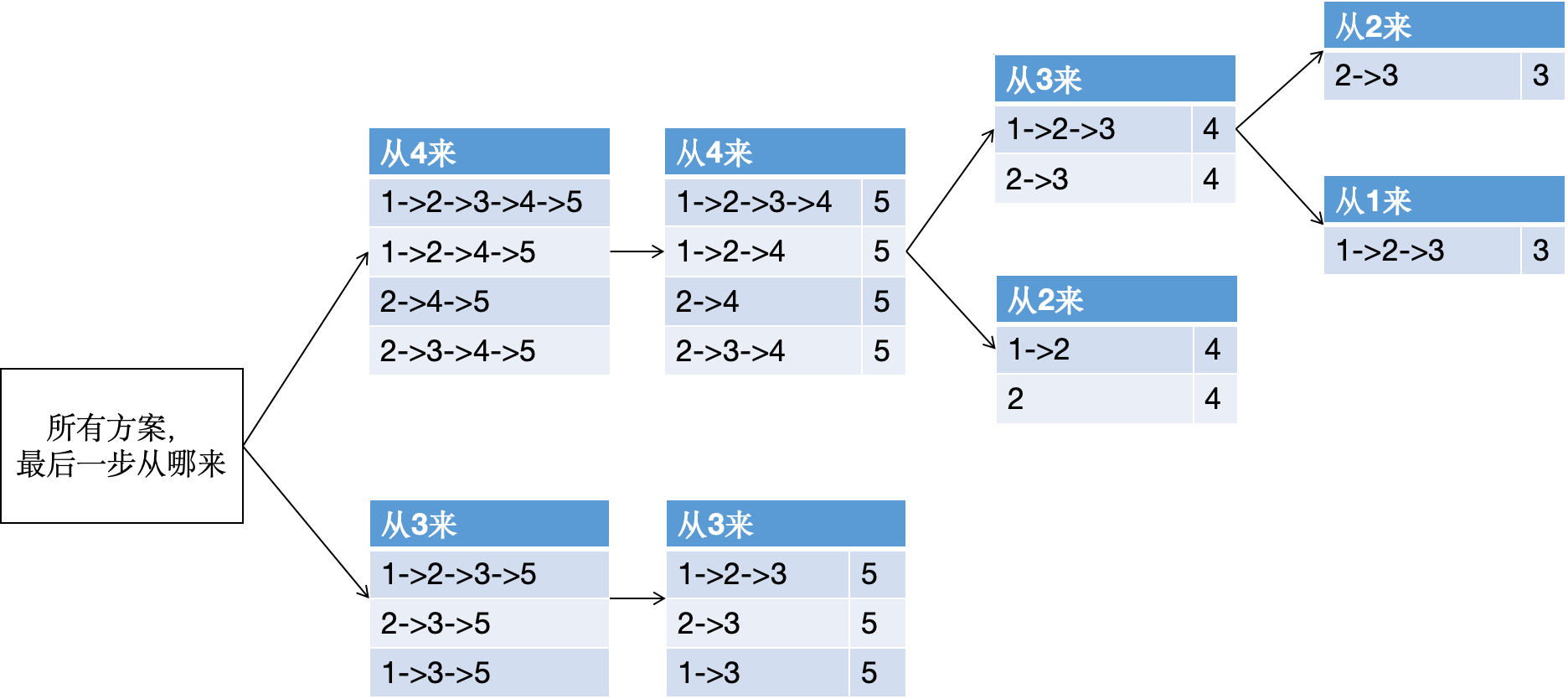
在这里插入图片描述
总之要想跳到第5阶，那么一定是从第3阶或者第4阶过来的，方案数也就是这两种集合方案数的和。我不知道跳到第4的阶的方案是什么，也不知道跳到第3阶的方案是什么，但是按照第3阶和第4阶，我可以将跳到第5阶所有的方案分成不重合的两个集合，只要求出这两个集合的方案数，然后相加就是最后的方案数。

这两个集合把所有的方案不重不漏的划分开来，符合无重叠性和完全覆盖性。第一个集合的所有方案，最后一步必然经过第4阶台阶，第二个集合的所有方案，最后一步必然经过第3阶台阶。

集合的唯一划分标准

这里有一个困惑，集合一中不是也会有方案经过3吗，为什么不会与集合二重叠呢？

两个集合的划分标准是 “最后一步的来源”，而非 “方案是否经过某个中间台阶”，因此即使集合一的方案经过 3 阶，也不会与集合二重叠

集合一（来自 n-1 阶）：所有方案的最后一步是 “从第 4 阶跳 1 阶到第 5 阶”（无论这个方案在到达 4 阶之前，是否经过 3 阶、2 阶等）。
例：方案 “1→2→3→4→5”，最后一步是 “4→5”，属于集合一；哪怕方案是 “1→3→4→5”，最后一步仍是 “4→5”，也属于集合一。
集合二（来自 n-2 阶）：所有方案的最后一步是 “从第 3 阶跳 2 阶到第 5 阶”（无论这个方案在到达 3 阶之前，是否经过 2 阶、1 阶等）。
例：方案 “1→2→3→5”，最后一步是 “3→5”，属于集合二；哪怕方案是 “1→3→5”，最后一步仍是 “3→5”，也属于集合二。

一个方案的 “最后一步” 是唯一的、不可拆分的，这是避免重叠的核心：