【高级机器学习】3. Convex Optimisation

Convex Optimisation

在机器学习中，优化问题的核心在于找到一个合适的假设 $h$，使得损失函数最小化。
这一节我们来系统介绍 凸优化 (Convex Optimisation) 的基本概念与方法。

---

Basics I: Convex Combination

• 给定两点 $x,y\in C\subseteq {\mathbb{R}}^d$，
  如果 $0\le \theta \le 1$，则
  $$\theta x+(1-\theta )y\in C$$
  称为 凸组合 (Convex Combination)。

---

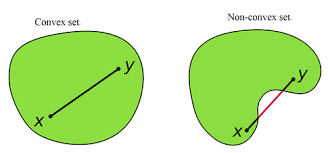
Basics I: Convex Set

• 定义：集合 $C\subseteq {\mathbb{R}}^d$ 是凸集，当且仅当对任意 $x,y\in C$，以及任意 $0\le \theta \le 1$，都有：
  $$\theta x+(1-\theta )y\in C$$

• 举例：

  • 凸集：球、半空间、区间等
  • 非凸集：环形、交错的集合等
    

---

Basics II: Convex Functions

定义

函数 $f:{\mathbb{R}}^d\to \mathbb{R}$ 称为凸函数，如果其定义域为凸集，且满足：
$$f(\theta x+(1-\theta )y)\le \theta f(x)+(1-\theta )f(y),\forall x,y\in \text{dom}f,\theta \in [0,1]$$

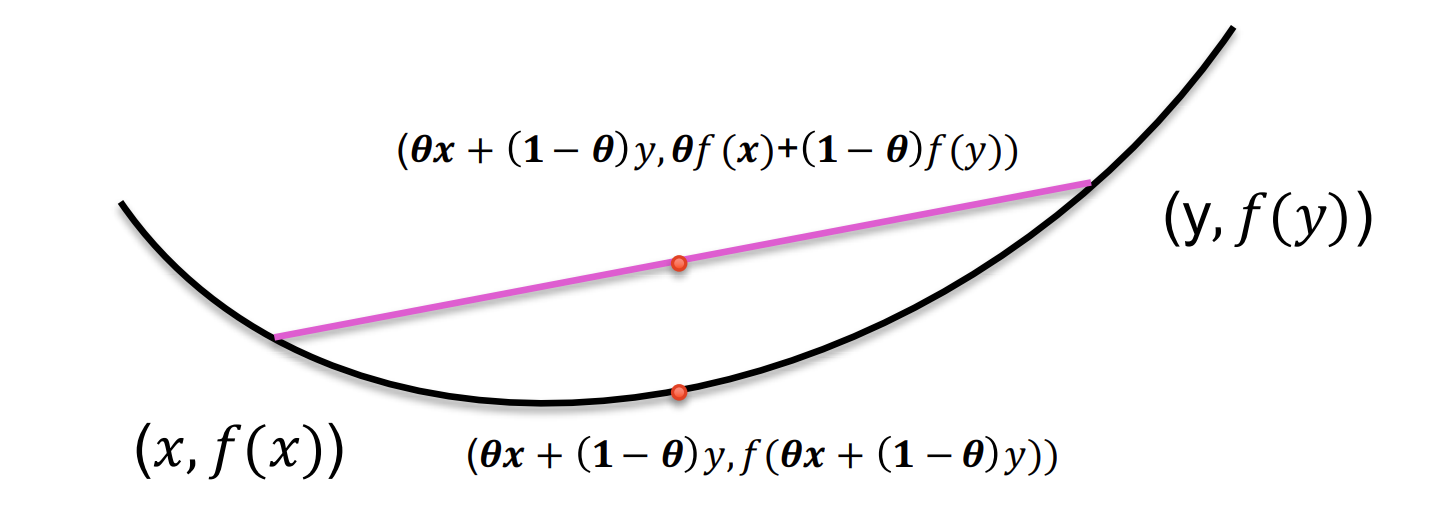
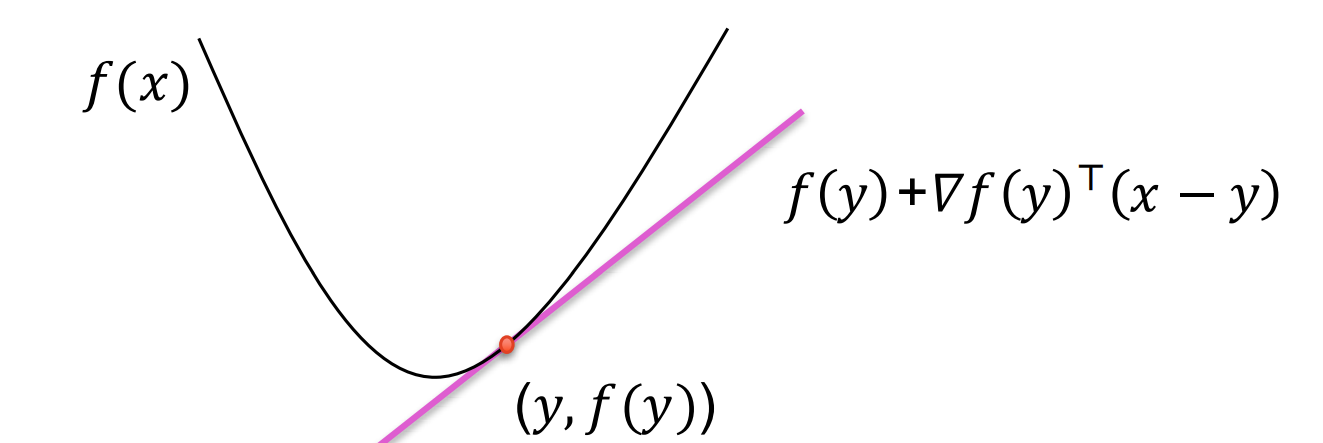
可微情况

若 $f$ 可微，则 $f$ 是凸函数当且仅当：
$$f(y)\ge f(x)+\nabla f(x{)}^{\top }(y-x),\forall x,y\in \text{dom}f$$

其中梯度：
$$\nabla f(x)=\left(\frac{\partial f}{\partial x_1},\dots ,\frac{\partial f}{\partial x_d}\right)$$

函数图像在切平面（切线）上方。

$f(x)+\nabla f(x{)}^{\top }(y-x)$ 就是点 $x$ 处的切线（或切平面）。

对凸函数来说，整个函数曲线都在这个切平面之上。

二阶可微情况

若 $f$ 二阶可微，则 $f$ 是凸函数当且仅当 Hessian 矩阵 半正定：
$${\nabla }^{2}f(x)⪰0,\forall x\in \text{dom}f$$
等价于所有特征值非负。

---

Basics III: 凸函数的闭合性

• 非负加权和：若 $f_1,f_2$ 是凸函数，则
  $$f(x)=\alpha f_1(x)+\beta f_2(x),\alpha ,\beta \ge 0$$
  仍是凸函数。

• 点对点最大值：
  f(x)=max⁡{f1(x),f2(x)} f(x) = \max \{ f_1(x), f_2(x) \} f(x)=max{f1​(x),f2​(x)}
  也是凸函数。

• 仿射变换复合：若 $f$ 是凸函数，$A$ 为矩阵，$b$ 为向量，则
  $$g(x)=f(Ax+b)$$
  仍是凸函数。

应用：SVM 的目标函数就是凸函数。

---

Unconstrained Convex Optimisation

问题形式

$$\underset{h\in \mathcal{H}}{\min }f(h)=\underset{h\in \mathcal{H}}{\min }\frac{1}{n}\sum _{i=1}^n\ell (X_i,Y_i,h)$$

其中 $\ell$ 是凸替代损失函数。

---

Taylor’s Theorem

若 $f:\mathbb{R}\to \mathbb{R}$ 在点 $a$ 处 $k$ 阶可导，则：
$$f(x)=f(a)+f^{\prime }(a)(x-a)+\cdots +\frac{f^{(k)}(a)}{k!}(x-a{)}^k+h_k(x)(x-a{)}^k$$
其中 ${\lim }_{x\to a}{h}_k(x)=0$。

示例

$f(x)=\frac{1}{6}{x}^3$，在 $a=1$ 展开：
$$f(x)=\frac{1}{6}+\frac{1}{2}(x-1)+\frac{1}{2}(x-1{)}^2+o((x-1{)}^2),x\to 1$$

---

Small-o Notation

记号 $f(x)=o(g(x)),x\to a$ 表示：
$$\underset{x\to a}{\lim }\frac{f(x)}{g(x)}=0$$

例如：
$$\frac{\frac{1}{6}{x}^3-\frac{1}{6}-\frac{1}{2}(x-1)-\frac{1}{2}(x-1{)}^2}{(x-1{)}^2}\to 0,x\to 1$$

---

Gradient Descent Method

通过泰勒展开：
$$f(h_{k+1})\approx f(h_k)+\eta \nabla f(h_k{)}^{\top }{d}_k+o(\eta )$$

若 $\nabla f(h_k{)}^{\top }{d}_k<0$，则 $f(h_{k+1})<f(h_k)$。

• 更新公式：
  $$h_{k+1}=h_k-\eta \nabla f(h_k)$$

---

下降方向与更新矩阵

一般形式：
$$h_{k+1}=h_k-\eta D_k\nabla f(h_k)$$

• 最速下降 (Steepest Descent)：$D_k=I$
• 牛顿法 (Newton’s Method)：$D_k=[{\nabla }^{2}f(h_k){]}^{-1}$
  • 常见改进：只取对角线、近似 Hessian（BFGS, L-BFGS）

---

学习率选择

• 精确线搜索 (Exact Line Search)：$\eta =\arg {\min }_{\eta }f(h_k-\eta \nabla f(h_k))$
  但通常计算代价太高。
• Lipschitz 光滑梯度：若存在常数 $L$ 使得
  $$\Vert \nabla f(x_1)-\nabla f(x_2)\Vert \le L\Vert x_1-x_2\Vert$$
  则取 $\eta =\frac{1}{L}$，保证：
  $$f(h_{k+1})\le f(h_k)-\frac{1}{2L}\Vert \nabla f(h_k){\Vert }^2$$

---

Gradient Convergence Rate

• 目标：找到最优解
  $$h^{\ast }=\arg \underset{h\in \mathcal{H}}{\min }f(h)$$

• 若 $f$ 是 强凸函数，且梯度 Lipschitz，则梯度下降具有 线性收敛率：
  $$f(h_{k+1})-f(h^{\ast })\le {\left(1-\frac{\mu }{L}\right)}^k\left(f(h_1)-f(h^{\ast })\right)$$

其中 $\mu$ 是强凸参数，$L$ 是 Lipschitz 常数。

---

收敛率总结表

算法	假设	收敛率
Gradient Descent	光滑梯度，凸函数	$O(1/k)$
Gradient Descent	光滑梯度，强凸函数	线性收敛 $(1-\mu /L{)}^k$
Newton’s Method	光滑梯度，强凸函数	二次收敛

---

Constrained Optimisation

一般的约束凸优化问题：
$$\underset{h\in \mathcal{H}}{\min }f(h),\text{s.t. }{g}_i(h)\le 0,h_j(h)=0$$

• $f,g_i$ 为凸函数
• $h_j$ 为仿射函数：$h_j(h)=a_j^{\top }h-b_j$

这是后续学习 拉格朗日对偶性 与 KKT 条件 的基础。

---