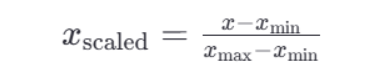当前位置：首页 > news >正文

机器学习：前篇

news 2025/8/27 15:01:02

一、机器学习介绍

定义

分类

监督学习

半监督学习

无监督学习

强化学习

二、scikit-learn

scikit-learn安装

三、数据集

sklearn本地的数据

网络上获取的数据

本地csv数据

数据集划分

四、特征工程

特征提取

字典列表特征提取

文本词频特征提取

文本稀有度提取

无量纲化

MinMaxScaler归一化

normalize归一化

StandardScaler标准化

特征降维

特征选择

VarianceThreshold 低方差过滤特征选择

根据相关系数的特征选择

主成分分析（PCA）

总结

一、机器学习介绍

定义

机器学习（Machine Learning）本质上就是让计算机自己在数据中学习规律，并根据所得到的规律对未来数据进行预测。

机器学习包括如聚类、分类、决策树、贝叶斯、神经网络、深度学习（Deep Learning）等算法。

二、scikit-learn

scikit-learn安装

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple scikit-learn

三、数据集

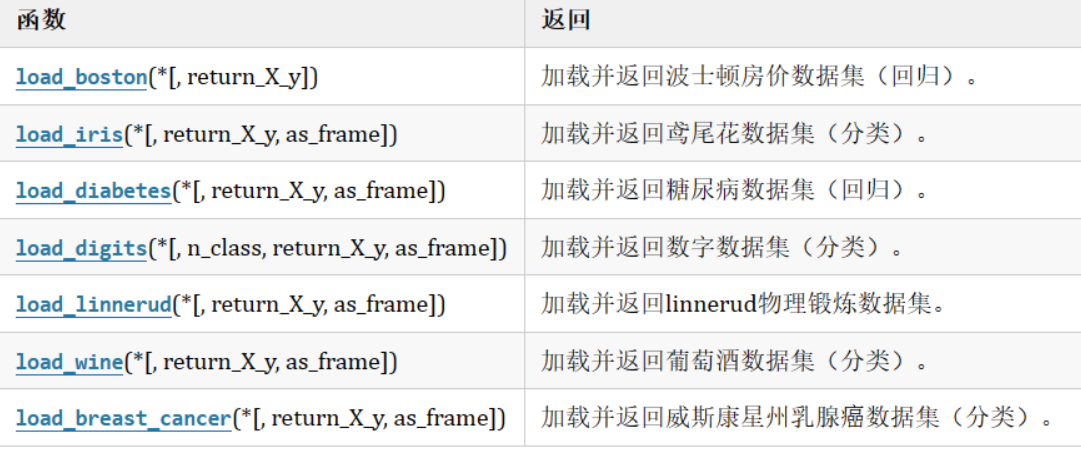
sklearn本地的数据

数据包含在sklearn库中

# 加载本地数据集
# 加载葡萄酒数据集
from sklearn.datasets import load_wine
wine = load_wine()

网络上获取的数据

from sklearn.datasets import fetch_lfw_pairs# 获取数据集
lfw_pairs = fetch_lfw_pairs(data_home='./data',subset='all')
print(lfw_pairs[0])

如果目录中已经存在，就直接读取，不会重复下载

本地csv数据

利用pands读取excel或csv格式文件

import pandas as pd
data_f = pd.read_excel('data.xlsx')

数据集划分

导包：
from sklearn.model_selection import train_test_split
函数：

sklearn.model_selection.train_test_split(*arrays，**options)

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_splitx,y = load_iris(return_X_y=True)   # 返回特征矩阵和标签向量# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)  # 测试集占比20%
print(x_train.shape, x_test.shape)
print(y_train.shape, y_test.shape)

可以自定义训练集和测试集的比例

可以同时对多个数据集进行划分，划分的比例一样

四、特征工程

特征提取

字典列表特征提取

导包：
from sklearn.feature_extraction import DictVectorizer
转换器：
transfer = DictVectorizer(sparse=True)    
True表示返回稀疏矩阵

from sklearn.feature_extraction import DictVectorizer
data = [{'name':'小王', 'age':18,'sex':'男'},{'name':'小李', 'age':20,'sex':'男'},{'name':'小周', 'age':17,'sex':'女'}]
# 创建转换器
transfer = DictVectorizer(sparse=True)  # sparse=False表示返回的是一个完整的矩阵,True表示返回的是一个稀疏矩阵
data = transfer.fit_transform(data)
print(data)
print(transfer.get_feature_names_out())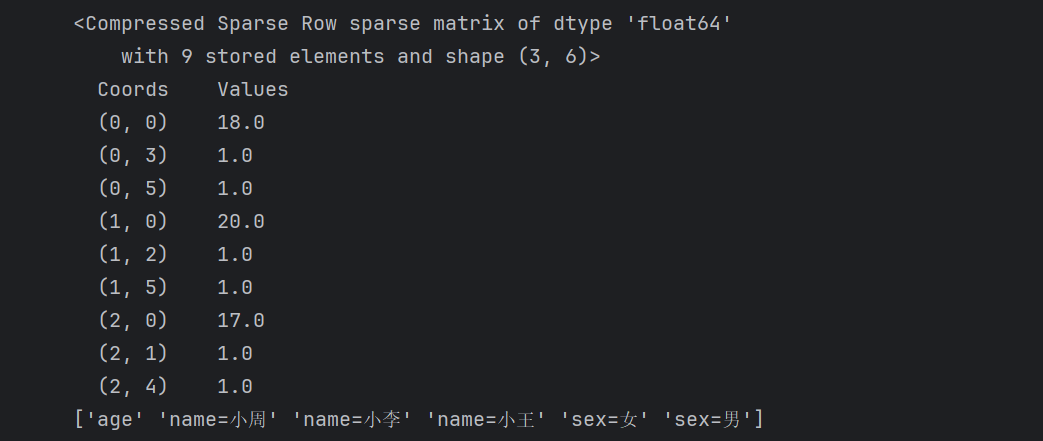

稀疏矩阵读取：

元组的第一个数字表示数据的序号索引，共三个数据（0，1，2）

元组的第二的数字表示下面特征（数组）的索引，如0对应age

最右列数据表示特征对应的数据或表示文本数据：如18表示age=18,第二个数1.0表示name=小周文本数据

文本词频特征提取

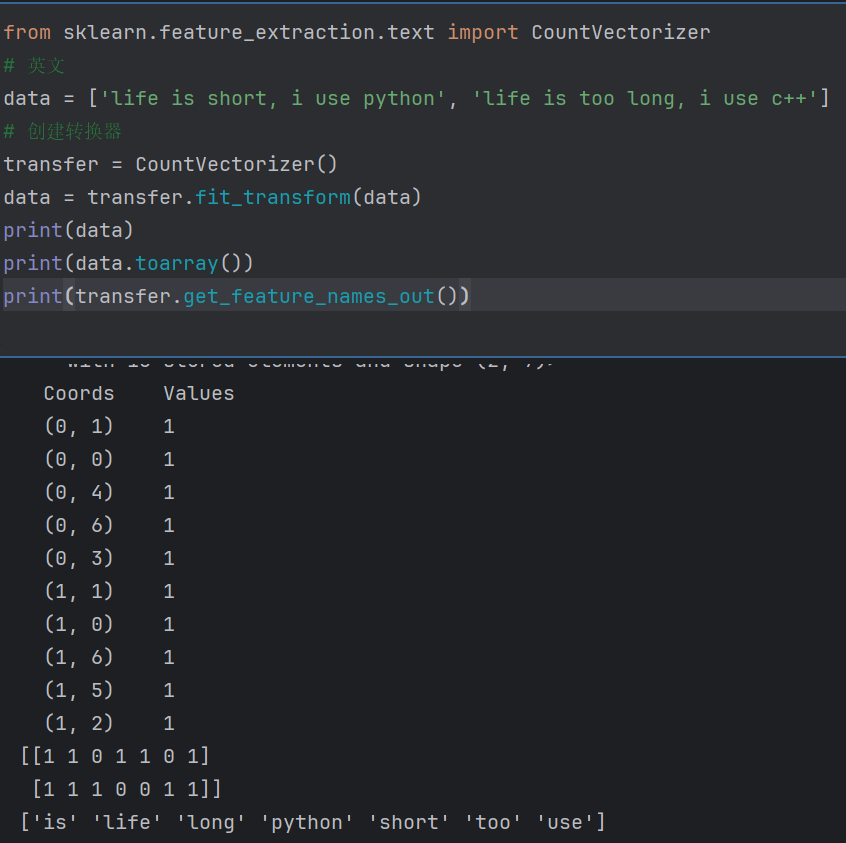
可以根据空格分割，但是中文词与词之间没有空格，所以需要手动加空格，太过麻烦，引入jieba的包来划分中文词频

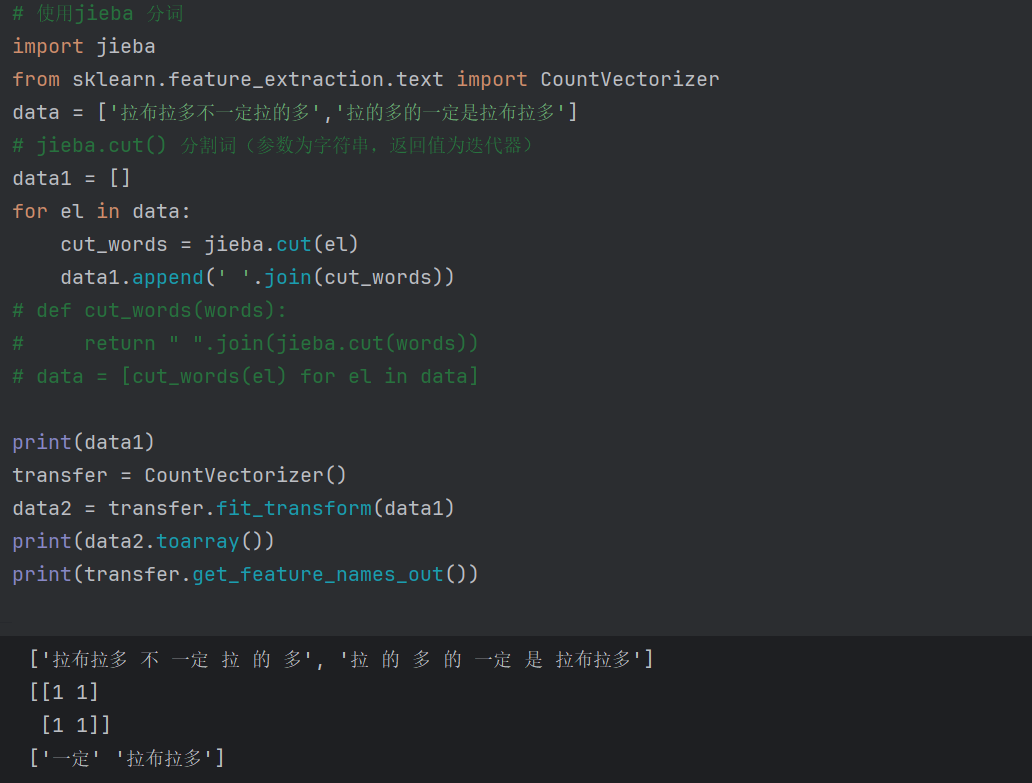
文本稀有度提取

导包：

sklearn.feature_extraction.text.TfidfVectorizer()

词频(TF), 表示一个词在当前篇文章中的重要性

逆文档频率(IDF), 反映了词在整个文档集合中的稀有程度

from sklearn.feature_extraction.text import CountVectorizer
import jieba
import numpy as np
from sklearn.preprocessing import normalize
data = ['拉布拉多 不一定是 拉的多','拉的多 的 一定是 拉布拉多']transfer = CountVectorizer()
data = transfer.fit_transform(data)
# print(data.toarray())
print(transfer.get_feature_names_out())
TF = data.toarray()
IDF = np.log((len(TF)+1)/(np.sum(TF!=0,axis=0)+1))+1
print(IDF)
TF_IDF = TF*IDFTF_IDF = normalize(TF_IDF,axis=1,norm='l2')
print(TF_IDF)

无量纲化

不同特征的数据数值范围不同，可能差距过大，一些重要的特征因为数值取值较小对计算结果影响较小，所以要对数据进行处理

MinMaxScaler归一化

公式：

归一化API

sklearn.preprocessing.MinMaxScaler(feature_range)

feature_range是归一化后的值域

缺点

最大值和最小值容易受到异常点影响，所以鲁棒性较差

normalize归一化

L1归一化：绝对值相加作为分母,特征值作为分子

L2归一化：平方相加作为分母,特征值作为分子

max归一化：max作为分母,特征值作为分子

导包：

from sklearn.preprocessing import normalize

API：
normalize(data, norm='l2', axis=1)

StandardScaler标准化

对每个特征的值减去其均值，再除以其标准差，将数据转换为均值为0，标准差为1的分布。

API：

from sklearn.preprocessing import StandardScaler

transfer = StandardScaler()
data_new = transfer.fit_transform(data)

特征降维

特征选择

VarianceThreshold 低方差过滤特征选择

如果一个特征的方差很小，说明这个特征的值在样本中几乎相同或变化不大，包含的信息量很少，可以去掉。

计算方差：对于每个特征，计算其在训练集中的方差(每个样本值与均值之差的平方,在求平均)。

设定阈值：选择一个方差阈值，任何低于这个阈值的特征都将被视为低方差特征。

过滤特征：移除所有方差低于设定阈值的特征

sklearn.feature_selection.VarianceThreshold(threshold=2.0) # 方差为等于小于2的去掉
VananceThreshold.fit_transform(x)

根据相关系数的特征选择

原理：皮尔逊相关系数，一种度量两个变量之间线性相关性的统计量

ρ=1 表示完全正相关，即随着一个变量的增加，另一个变量也线性增加。

ρ=-1 表示完全负相关，即随着一个变量的增加，另一个变量线性减少。

ρ=0 表示两个变量之间不存在线性关系。

|ρ|<0.4为低度相关; 0.4<=|ρ|<0.7为显著相关； 0.7<=|ρ|<1为高度相关

API:

from scipy.stats import pearsonr

personr(x, y)

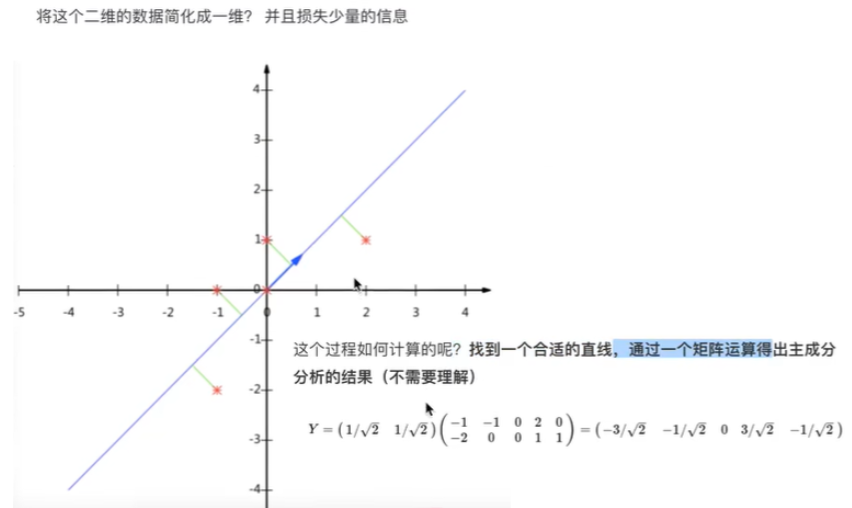
主成分分析（PCA）

PCA的核心目标是从原始特征空间中找到一个新的坐标系统，使得数据在新坐标轴上的投影能够最大程度地保留数据的方差，同时减少数据的维度。

简单理解就是把一个原始特征按信息量进行相互融合，转换为低维度的特征，保留了信息特征，但不再直观，比如将 "长、宽、高" 转换为 "体积相关成分" 和 "形状相关成分"

API:

from sklearn.decomposition import PCA

PCA(n_components=None)

主成分分析

n_components:

实参为小数时：表示降维后保留百分之多少的信息

实参为整数时：表示减少到多少特征