HMM简单拓展-HSMM与高阶HMM
HMM就不用介绍了,在机器学习火起来以前,生物信息领域凡是涉及到序列分析的问题,基本上都可以使用HMM来解决。
上到基因结构注释,下到序列比对,可以说HMM是经典生信派的万金油模型。
一,HSMM(hidden semi-Markov model,隐半马尔科夫模型)
参考:https://en.wikipedia.org/wiki/Hidden_semi-Markov_model


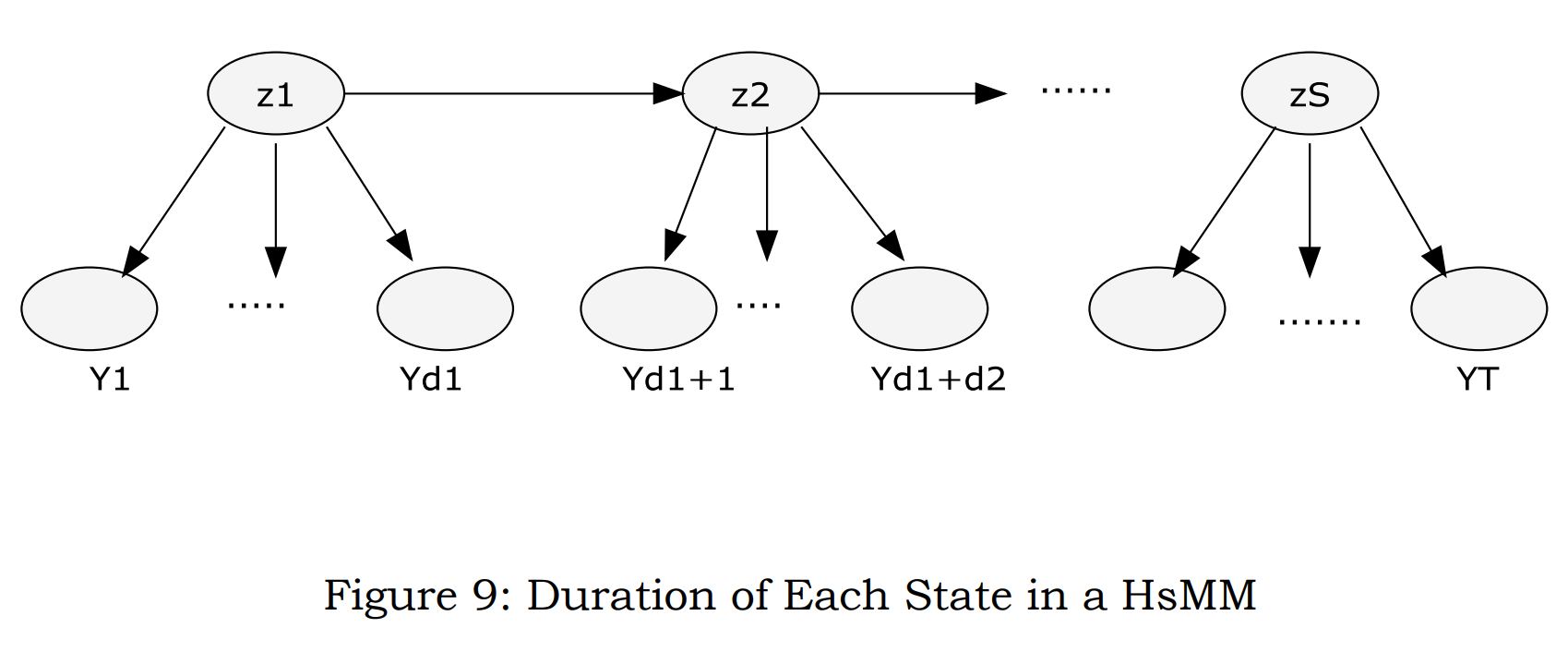
wiki太简略了,我们直接上model示意图,需要联系一般HMM的model结构,来进行比对分析:
1,model示意图


简而言之,HSMM是HMM的扩展,允许(隐)状态具有可变的时长,可以更好地建模时间上的不确定性,
对应的就是隐状态多了个与状态时间相关的分布变量,然后相关的建模方面相比一般的HMM就需要考虑状态和时长的联合概率。
2,model参数化结构
在model构建方面,和一般的HMM一样,也有:
(1)初始状态分布
初始状态为状态i的概率是πi

(2)状态转移概率
t时刻状态为i,下一时刻转移到状态j的概率为aij
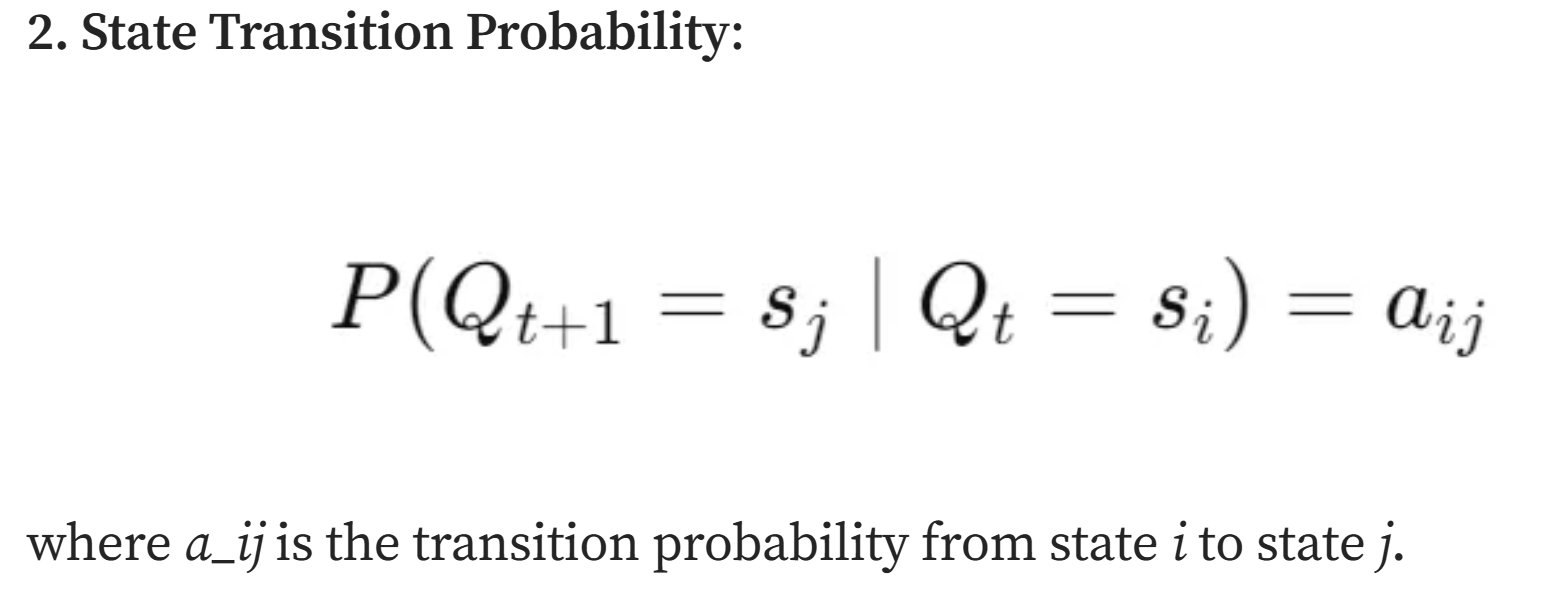
(3)发射概率
t时刻隐状态为i,发射显状态为ok的概率为bik
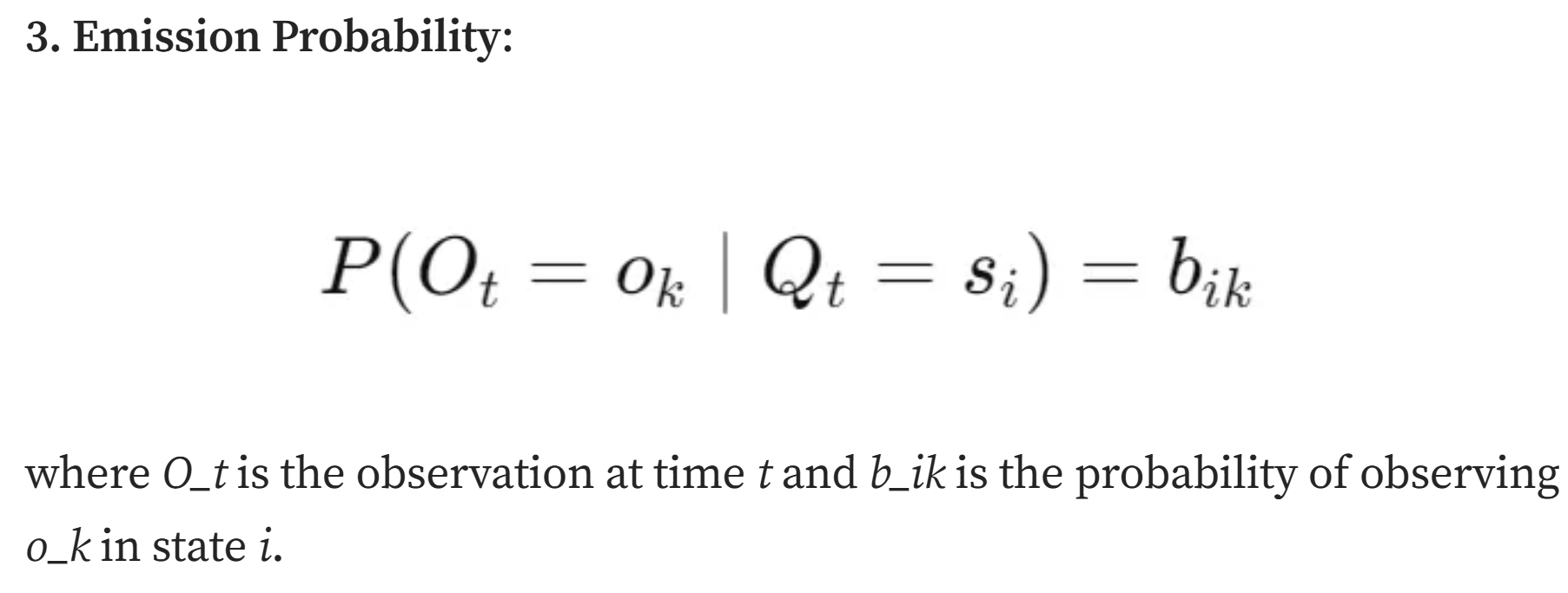
(4)隐状态持续时间概率分布
t时刻状态为i,持续d时间步的概率为pik
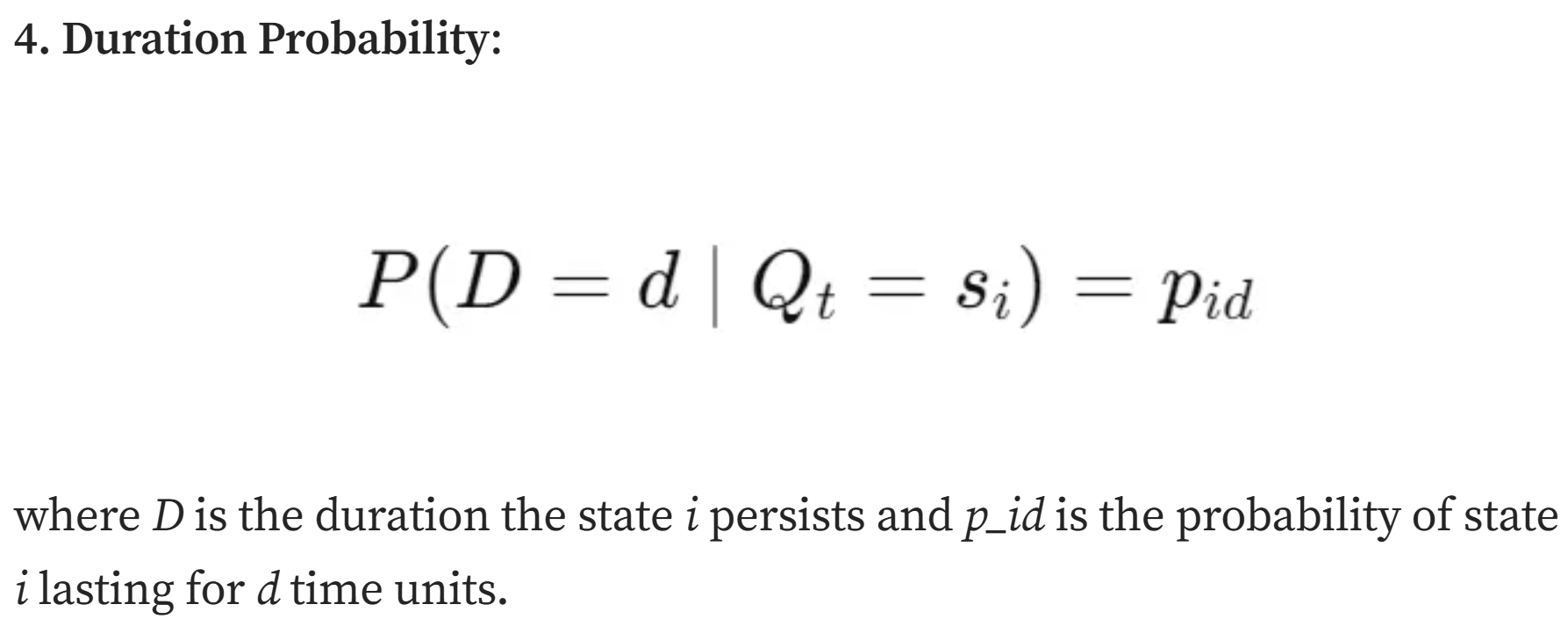
3,model相关算法
我们知道,一般的HMM模型,有3个经典问题,分别有相应的算法去解决,同样的,HSMM也有。

以Forward-Backward Algorithm为例:
前向-后向算法是一种动态规划算法,用于计算在给定观测序列时,HSMM中某个状态序列的后验概率。
具体推导方法和李航老师的统计学习方法中一般HMM模型逻辑一致:


示例分析参考:https://medium.com/@karishmaagarwal2505/extending-hidden-markov-models-the-role-of-hidden-semi-markov-models-in-modern-data-analysis-97cf0a5de3f6

以概率1开始在第一个状态

没有状态自转移

这个矩阵比较重要,是隐状态的持续时间分布矩阵,规定了在每个状态中停留时间的概率分布。
比如说上图这个矩阵,第1个状态有50%的概率持续1或2个时间单位(时间步,time unit);
第2个状态有50%的概率持续1个时间单位,70%的概率持续3个时间单位等。

概率发射矩阵,表示从每个隐状态观察到每个可能(显状态)输出的概率。
4,HMM与HSMM的主要区别
(1)状态持续时间:
HMM:假设状态持续时间服从几何分布,隐式地模拟了指数持续时间分布。
HSMM:允许使用更灵活的分布显式地对状态持续时间进行建模。
(2)model复杂度:
HMM:参数更少、更简单的model,适用于具有指数状态持续时间的过程。
HSMM:更复杂,具有用于用于持续时间分布的附加参数,更适合于具有非指数状态持续时间的过程。
总的来说,HMM适用于状态持续时间变化不大的简单时间序列数据,而HSMM更适用于持续时间变化显著且需要明确建模的复杂序列,适用于状态持续时间并非指数分布的广泛过程(灵活的状态持续时间建模)。
(3)总结:
我们知道HMM本质上是满足马尔科夫性质的随机过程,只不过是在状态空间中切换的这条马尔科夫链,一些最基本的参数是hidden的,需要建模推断。
常用的是一阶HMM,有简单的无后效性假设,也就是假设当前状态仅仅依赖于前面1个状态的随机变量的取值,这个简化的假设应用实际上比较受限。
实际在生物序列建模中,尤其是时间序列建模中,要考虑到你假设的计算生物研究对象的生成,比如说某个feature,在sequence层面上生成是否是只依赖于前面一个sequence token/state的feature,
如果假设不成立,或者是与真实生物学信号联系思考之后是不可能的话,就得抛弃1阶HMM了;
当然,从研究的角度来讲,建模本身是从易到难,我们数理化中有各种各样的解决主要矛盾忽略次要矛盾的建模,比如说质点忽略形状,所以建模仅仅只从考虑一阶HMM,至少在初步的建模是无可厚非的。
从统计学习的角度来看,HSMM与HMM的主要区别在于对隐状态持续时间的建模方式。
我们从HMM模型架构最基本的3个参数出发:
初始状态概率分布、隐状态转移矩阵、观测状态发射矩阵。
从统计学习的角度来看,隐半马尔可夫模型(HSMM)与隐马尔可夫模型(HMM)的主要区别在于对隐状态持续时间的建模方式。以下是基于模型结构和三个参数(初始状态概率分布、隐状态转移矩阵、观测状态发射矩阵)的详细比较分析
模型结构
- HMM:假设隐状态的持续时间遵循几何分布(所谓几何分布,意味着每个隐状态在每个时间步上都有一个固定的概率p转移到其他状态,而与该状态已经持续了多长时间无关),即在任意时刻,隐状态转移的概率是恒定的,与该状态已经持续的时间无关。这种假设简化了模型,但可能不适用于所有实际场景。
- HSMM:允许隐状态的持续时间遵循更复杂的分布(如泊松分布、指数分布等),并且状态转移概率可以依赖于当前状态已经持续的时间。这使得HSMM能够更灵活地建模隐状态的持续时间,适用于那些隐状态持续时间不符合几何分布的场景。

初始状态概率分布
- HMM:初始状态概率分布
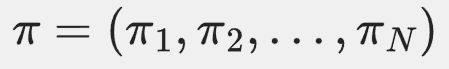 表示隐状态在初始时刻处于各个状态的概率。这个分布对于HMM和HSMM是相同的,因为它们都描述了初始时刻隐状态的概率分布。
表示隐状态在初始时刻处于各个状态的概率。这个分布对于HMM和HSMM是相同的,因为它们都描述了初始时刻隐状态的概率分布。 - HSMM:初始状态概率分布与HMM相同,但HSMM在建模时需要额外考虑隐状态的持续时间分布。因此,在实际应用中,HSMM的初始状态概率分布需要结合隐状态的持续时间分布来解释模型的行为。
隐状态转移矩阵
- HMM:隐状态转移矩阵
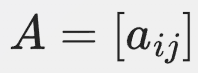 ,其中
,其中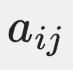 表示从隐状态 (i) 转移到隐状态 (j) 的概率。在HMM中,这个转移概率是恒定的,与当前状态已经持续的时间无关。
表示从隐状态 (i) 转移到隐状态 (j) 的概率。在HMM中,这个转移概率是恒定的,与当前状态已经持续的时间无关。 - HSMM:隐状态转移矩阵在HSMM中变得更加复杂。HSMM引入了持续时间分布,因此转移概率不仅取决于当前状态,还取决于当前状态已经持续的时间。这意味着HSMM的转移矩阵需要根据持续时间进行动态调整。例如,如果一个隐状态已经持续了较长时间,其转移概率可能会增加,以反映状态变化的可能性。
- 简单理解就是HMM的转移矩阵A是固定的,与时间无关;而HSMM的转移矩阵A是时间的函数,与当前状态已经持续的时间有关。

也就是需要引入一个新的随机变量,状态的持续概率。
观测状态发射矩阵
- HMM:观测状态发射矩阵
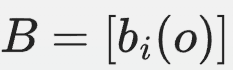 ,其中
,其中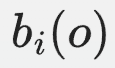 表示在隐状态 (i) 下观测到观测状态 (o) 的概率。在HMM中,发射概率只依赖于当前隐状态,而与隐状态的持续时间无关。
表示在隐状态 (i) 下观测到观测状态 (o) 的概率。在HMM中,发射概率只依赖于当前隐状态,而与隐状态的持续时间无关。 - HSMM:在HSMM中,观测状态发射矩阵的定义与HMM相同,但HSMM的发射概率可以结合隐状态的持续时间分布来解释。例如,如果一个隐状态持续时间较长,其发射概率可能会受到持续时间的影响,从而更准确地反映观测数据的生成过程。
5,Implementation实现
对于HMM,我之前有篇博客讨论过一阶HMM(连续、离散隐状态取值)的实现,
有监督的、无监督的都有工程化比较完备、甚至是非常成熟的轮子,
无监督的框架,比如说我常用的hmmlearn,有监督的框架,比如说seqlearn。
参考:https://github.com/hmmlearn/hmmlearn

对于HSMM,python库有:
https://hsmmlearn.readthedocs.io/en/latest/index.html
https://github.com/jvkersch/hsmmlearn

R包也有:不过已经从CRAN中移除了
https://cran.r-project.org/src/contrib/Archive/hsmm/
对于实现的原理部分,对数学感兴趣的,可以详细参考下面这本书:
https://oasis.library.unlv.edu/cgi/viewcontent.cgi?article=1998&context=thesesdissertations

二,High-order HMM 高阶HMM(HOHMM)
这个其实就很容易理解了,我们通常使用的是一阶HMM,也就是当前时间步隐状态随机变量的取值分布,只取决于前1个时间步的随机变量的取值分布,但是实际过程中,尤其是对于一条时间序列建模过程来讲,当前时刻的取值分布,可能需要取决于前2个、3个甚至是n个时间步的状态信息;
这个时候,我们就需要高阶HMM模型,阶数(order rank),指的就是需要参考前多少个时间步的状态信息。
理论方面,其实很早就有人做过分析,能够将任何高阶HMM(包括状态序列和观测序列依赖性为不同阶数的model)转换为等效的一阶HMM,从而使一阶HMM公式适用于任何阶数model。
比如说参考:https://ieeexplore.ieee.org/document/5278591
另外对于特定任务的单纯开发实现,其实也有,
比如说:https://simple-hohmm.readthedocs.io/en/latest/
https://github.com/jacobkrantz/Simple-HOHMM
但总的来说,从实践角度上看,高阶HMM的实现比较复杂。
但是,别忘了,我们一直在讨论的是经典机器学习,那已经是几十年前的理论了。
现在如果要解决多个时间状态信息都考虑入内的问题,其实我们可以使用深度学习模型,比如说RNN,或者是transformer等模型,从某种程度上说,都算是优化之后、考虑到了Global receptor field的时间步状态信息。
这其实是时间序列建模中的经典问题需求:更精细的建模,需要考虑更多时间步的状态信息。
高阶HMM通过扩展状态转移概率来增加感受野,从而能够捕捉更复杂的依赖关系。RNN和Transformer则通过不同的机制(递归更新和自注意力)来增加感受野,从而更有效地处理时间序列数据。
1. 高阶HMM与自回归模型的关系
自回归模型(AR)
自回归模型是一种统计模型,用于描述时间序列中当前值与过去若干个时间步值之间的线性关系。一个 ( p ) 阶自回归模型(AR§)可以表示为:
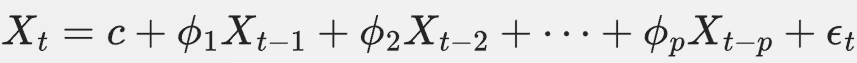
其中:

高阶HMM
高阶HMM是传统HMM的扩展,它允许当前状态不仅依赖于前一个状态,还可以依赖于前多个状态。一个 ( n ) 阶HMM可以表示为:
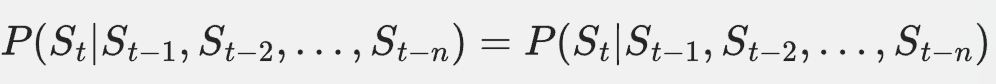
其中:

从数学角度来看,高阶HMM通过考虑多个时间步的状态信息来预测当前状态,这与自回归模型通过考虑多个时间步的观测值来预测当前值有相似之处。因此,高阶HMM可以被视为一种特殊的自回归模型,其中隐藏状态的转移概率依赖于前多个时间步的状态。
2. 高阶HMM在时间序列建模中的考虑
在时间序列建模中,高阶HMM通过扩展状态转移概率来考虑当前多个时间步状态的信息。具体来说,高阶HMM的转移概率矩阵 ( A ) 不再是一个简单的二维矩阵,而是一个更高维度的张量。例如,一个二阶HMM的转移概率可以表示为:
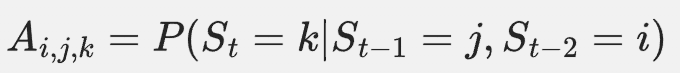
这意味着当前状态 ( S_t ) 的转移概率不仅依赖于前一个状态 ( S_{t-1} ),还依赖于前两个状态 ( S_{t-2} )。
通过这种方式,高阶HMM能够捕捉更复杂的依赖关系,从而更准确地建模时间序列数据。然而,这种扩展也带来了计算复杂度的增加,因为需要估计更多的参数。
3. 与RNN和Transformer的联系
循环神经网络(RNN)
RNN是一种神经网络架构,专门用于处理序列数据。RNN通过在每个时间步更新隐藏状态来捕捉时间序列中的依赖关系。RNN的更新公式可以表示为:
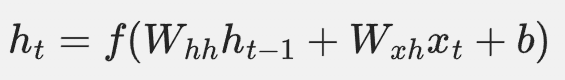
其中:

RNN可以被视为一种动态系统,其中隐藏状态 ( h_t ) 依赖于前一个隐藏状态 ( h_{t-1} ) 和当前输入 ( x_t )。这与HMM中的状态转移有相似之处,但RNN通过神经网络的非线性变换来捕捉更复杂的依赖关系。
Transformer
Transformer是一种基于自注意力机制的神经网络架构,广泛用于自然语言处理和其他序列建模任务。Transformer通过计算输入序列中每个位置的加权和来捕捉序列中的依赖关系。Transformer的自注意力机制可以表示为:
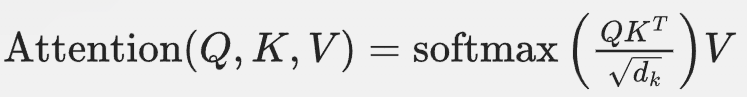
其中:

Transformer通过自注意力机制能够同时考虑序列中所有位置的信息,从而捕捉长距离依赖关系。这与高阶HMM通过考虑多个时间步的状态信息来建模有相似之处,但Transformer通过自注意力机制能够更高效地处理长序列。
4. 从感受野(Receptor Field)的角度
感受野(Receptor Field)是指神经网络中每个神经元能够感知的输入区域的大小。在时间序列建模中,感受野的大小决定了模型能够捕捉的时间序列中的依赖范围。
- 高阶HMM:通过扩展状态转移概率来增加感受野,从而能够捕捉更长距离的依赖关系。
- RNN:通过递归更新隐藏状态来增加感受野,但RNN的感受野是有限的,因为梯度消失或爆炸问题会限制其捕捉长距离依赖的能力。
- Transformer:通过自注意力机制,Transformer的感受野可以覆盖整个输入序列,从而能够高效地捕捉长距离依赖关系。
从某种程度上讲,高阶HMM也只不过是自回归model的一种特殊情况,对机器学习理论感兴趣的,可以从数学角度、从数学本质上去认知并理解HMM与现在的经典深度学习模型的区别与联系。
