支持向量机（SVM）核心概念总结

一、SVM 的基本思想

支持向量机（Support Vector Machine, SVM）是一种经典的监督学习算法，主要用于分类任务。其基本思想是：在样本空间中找到一个划分超平面，将不同类别的样本分开。

二、理想中的超平面

SVM 不仅要求分类正确，还希望找到一个容忍性最好的超平面，即：

对训练样本的局部扰动具有最强的鲁棒性

这意味着超平面应该尽可能远离两类样本点，从而提升模型的泛化能力。、

三、优化目标：最大化间隔（Margin）

SVM 的优化目标是最大化分类间隔（Margin），即两类样本中距离超平面最近的样本点（支持向量）到超平面的距离之和最大。

四、支持向量（Support Vectors）

支持向量是那些距离超平面最近的样本点，它们决定了超平面的位置和方向。换句话说，SVM 的训练结果仅由支持向量决定，与其他样本点无关。

五、超平面的数学表示

超平面是 n 维空间中的一个 𝑛−1维子空间。

例如：三维空间中的超平面是二维平面，二维空间中的超平面是一维直线。

超平面可以用线性方程表示：

其中：
w 是法向量，决定超平面的方向
b 是偏置项，决定超平面的位置

六、点到超平面的距离

点 x 到超平面的距离公式为：d=，该距离是SVM中“间隔”计算的基础。

七、实战演练

导入必要的库：

读取数据：

提取特征和目标变量：

对分类特征进行编码：

 划分训练集和测试集：

数据标准化：

创建 SVM 模型并训练模型：

在测试集上进行预测：

评估模型：

运行结果：

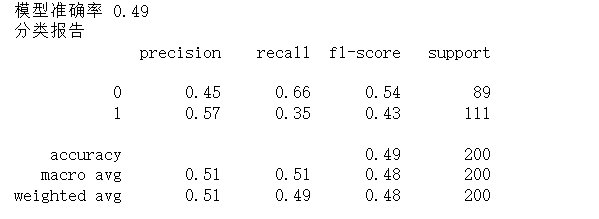
八、总结要点

SVM 的核心是最大化分类间隔，提升模型泛化能力​​

支持向量是决定模型的关键样本

超平面由法向量 w 和偏置 b 定义