【无标题】计数组合学7.21（有界部分大小的平面分拆)

7.21 有界部分大小的平面分拆

本节的主要目标是在 $q=1$ 的情况下细化定理 7.20.1，通过限制平面分拆 $\pi \in P(r,c)$ 的最大部分的大小。例如，考虑特殊情况 $r=1$，此时 $\pi$ 只是一个不超过 $c$ 个部分的普通分拆 $\lambda =({\lambda }_1,\dots ,{\lambda }_c)$。如果我们添加限制 ${\lambda }_1\le t$，那么命题 1.7.3 告诉我们
$$\sum _{\begin{array}{c}\lambda =({\lambda }_1,\dots ,{\lambda }_c)\\ {\lambda }_1\le t\end{array}}{q}^{|\lambda |}=\left(\genfrac{}{}{0ex}{}{c+t}{c}\right),$$
一个 $q$-二项式系数。正是这个结果，我们希望推广到平面分拆。我们不能期望像定理 7.20.1 那样有一个好的双射证明，因为即使在 $r=1$ 的情况下，$q$-二项式系数 $\left(\genfrac{}{}{0ex}{}{c+t}{c}\right)$ 的分子 $(1-q^{c+t})\cdots (1-q^{t+1})$ 的展开式也含有负系数。一个双射证明将不得不涉及对合原理论证（或类似的东西），或者将 $\left(\genfrac{}{}{0ex}{}{c+t}{c}\right)$ 的分子移到另一边。虽然这样的证明确实存在，但它们缺乏定理 7.20.1 证明的优雅。我们这里给出的证明不是双射的，但它将是对称函数理论的一个简单推论。

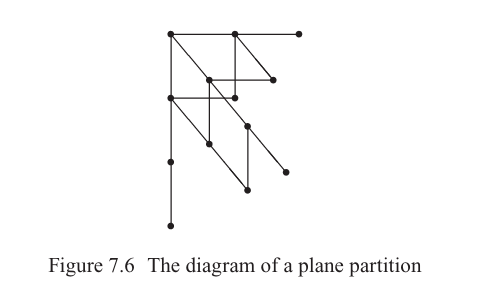
为了更好地理解对行数、列数和最大部分的限制的意义，我们首先讨论平面分拆的图的概念，推广分拆的杨图或 Ferrers 图的概念。形式上，平面分拆 $\pi =({\pi }_{ij})$ 的图 $D(\pi )$（通常等同于 $\pi$) 是 ${\mathbb{P}}^3$ 的子集，定义为
$$D(\pi )=\{(i,j,k)\in {\mathbb{P}}^3:1\le k\le {\pi }_{ij}\}.$$
可以想象用 ${\pi }_{ij}$ 个立方体（或点）的柱子代替元素 ${\pi }_{ij}$。例如，平面分拆
$$\pi =\begin{array}{ccc}4& 2& 1\\ 3& 1& \\ 1& & \\ 1& & \end{array}$$
的 (Ferrers) 图由图 7.6 给出。

三个坐标轴的任意置换 $w$ 将 $n$ 的平面分拆 $\pi$ 的图变换为另一个 $n$ 的平面分拆 $w(\pi )$。因此，一个平面分拆有六个“伴随”，称为关联形式 (aspects)，由 ${\mathfrak{S}}_3$ 的元素索引。与普通分拆 $\lambda$ 的两个“伴随” $\lambda$ 和 ${\lambda }^{\prime }$ 比较。就平面分拆 $\pi =({\pi }_{ij})$ 本身而言，六个关联形式按如下方式获得：

• 保持 $\pi$ 不变
• 对 $\pi$ 的每一行取共轭
• 对 $\pi$ 的每一列取共轭
• 转置 $\pi$
• 对 $\pi$ 的每一行取共轭然后转置
• 对 $\pi$ 的每一列取共轭然后转置。

当我们取 $\pi$ 的一个关联形式 $w(\pi )$ 时，三个统计量 ${\ell }_1(\pi )$, ${\ell }_2(\pi )$ 和 $\max (\pi )$ 在它们之间进行置换。因此，例如，具有最多 $r$ 行和最多 $c$ 列的 $n$ 的平面分拆数等于具有最多 $c$ 行且最大部分最多为 $r$ 的 $n$ 的平面分拆数。由于我们已经枚举了具有最多 $r$ 行和最多 $c$ 列的 $n$ 的平面分拆（定理 7.20.1 当 $q=1$ 时），现在考虑对最大部分的额外限制似乎非常自然。

令 $r,c,t\in \mathbb{P}$，并定义盒子
$$B(r,c,t)=\{(i,j,k)\in {\mathbb{P}}^3:1\le i\le r,1\le j\le c,1\le k\le t\}.$$
因此，一个平面分拆 $\pi$ 满足 ${\ell }_1(\pi )\le r$, ${\ell }_2(\pi )\le c$ 和 $\max (\pi )\le t$ 当且仅当它的图包含在盒子 $B(r,c,t)$ 中，我们将其写为 $\pi \subseteq B(r,c,t)$。那么，我们当前的目标是计算生成函数 ${\sum }_{\pi \subseteq B(r,c,t)}{q}^{|\pi |}$.

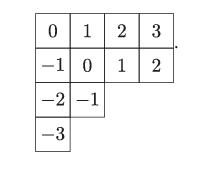
作为预备步骤，我们将计算主特化 $s_{\lambda }(1,q,\dots ,q^{n-1})$。这个结果的最优雅表述涉及与分拆的杨图方格相关的两个重要统计量。给定一个杨图 $\lambda$（这里我们将图 $\{(i,j):1\le j\le {\lambda }_i\}$ 与其形状视为等同）和一个方格 $u=(i,j)\in \lambda$，定义 $\lambda$ 在 $u$ 处的钩长 (hook length) $h(u)$ 为
$$h(u)={\lambda }_i+{\lambda }_j^{\prime }-i-j+1.$$
等价地，$h(u)$ 是在 $u$ 正右方或正下方的方格数，$u$ 本身计一次。例如，分拆 4221 的钩长由下式给出

类似地，定义 $\lambda$ 在 $u=(i,j)$ 处的内容 (content) $c(u)$ 为
$$c(u)=j-i.$$
对于 $\lambda =4221$，内容由下式给出

7.21.1 引理

设 $\lambda =({\lambda }_1,\dots ,{\lambda }_n)\in Par$ 且 ${\mu }_i={\lambda }_i+n-i$。则
$$\prod _{u\in \lambda }[h(u)]=\frac{{\prod }_{i\ge 1}[{\mu }_i]!}{{\prod }_{1\le i<j\le n}[{\mu }_i-{\mu }_j]}\text{\hspace{1em}(7.102)}$$
$$\prod _{u\in \lambda }[n+c(u)]=\prod _{i=1}^n\frac{[{\mu }_i]!}{[n-i]!},\text{\hspace{1em}(7.103)}$$
其中 $[k]=1-q^k$ 且 $[k]!=[1][2]\cdots [k]$.

证明. 相信“一图胜千言”，我们将用一个例子说明证明。设 $\lambda =4421$。在 $\lambda$ 图的第 $i$ 行添加 $n-i$ 个方格，得到 $\mu$ 的图。在方格 $(i,j)$ 中插入数字 ${\mu }_i-j+1$。因此，插入数字的多重集正好是 ⋃i≥1{1,2,…,μi}\bigcup_{i \geq 1} \{1, 2, \ldots, \mu_i\}⋃i≥1​{1,2,…,μi​}，即方程 (7.102) 右边（当写成因子 $1-q^k$ 的乘积时）分子中的指数。对于每个 $1\le i<j\le n$，将数字 ${\mu }_i-{\mu }_j$ 以粗体写在方格 $(i,{\mu }_j+1)$ 中。我们得到数组

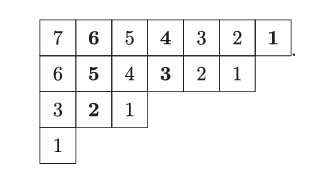
稍加思考可以看出，如果我们去掉粗体数字所在的第 ${\mu }_j+1$ 列，我们得到的正好是 $\lambda$ 的图，其中方格 $u$ 中写着钩长 $h(u)$。这就证明了 (7.102)。

一个类似（但更简单）的论证适用于方程 (7.103)。这里相关的数组是

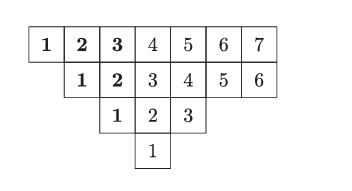
证明完成。 ∎

给定 $\lambda ⊢n$，定义
$$b(\lambda )=\sum (i-1){\lambda }_i=\sum \left(\genfrac{}{}{0ex}{}{{\lambda }_i^{\prime }}{2}\right).$$
注意，$b(\lambda )$ 是一个形状为 $\lambda$ 的 SSYT（允许 0 作为部分）的项和的最小可能值，它通过在 $\lambda$ 的第 $i$ 行的所有方格中放置 $i-1$ 而唯一获得。特别地，对于 $n\ge \ell (\lambda )$，我们有 $s_{\lambda }(1,q,\dots ,q^{n-1})=q^{b(\lambda )}{v}_{\lambda }(q)$，其中 $v_{\lambda }(q)$ 是一个满足 $v_{\lambda }(0)=1$ 的 $q$ 的多项式。（如果 $n<\ell (\lambda )$ 那么 $s_{\lambda }(1,q,\dots ,q^{n-1})=0$。)

7.21.2 定理

对于任意 $\lambda \in \text{Par}$ 和 $n\in \mathbb{P}$，我们有
$$s_{\lambda }(1,q,\dots ,q^{n-1})=q^{b(\lambda )}\prod _{u\in \lambda }\frac{[n+c(u)]}{[h(u)]}.$$

证明. 如果 $n<\ell (\lambda )$ 那么两边均为零，所以假设 $n\ge \ell (\lambda )$。由定理 7.15.1 ($s_{\lambda }(x_1,\dots ,x_n)$ 的双交错公式)，我们有
$$s_{\lambda }(1,q,\dots ,q^{n-1})=\frac{\det {\left(q^{(i-1)({\lambda }_j+n-j)}\right)}_{i,j=1}^n}{\det {\left(q^{(i-1)(n-j)}\right)}_{i,j=1}^n}.$$
分母正好是 Vandermonde 行列式 $a_{\delta }=\det \left(x_j^{n-i}\right)={\prod }_{1\le i<j\le n}(x_i-x_j)$ 的特化，因此等于 ${\prod }_{1\le i<j\le n}\left(q^{i-1}-q^{j-1}\right)$。但分子也是 $a_{\delta }$ 的特化，尽管有些伪装。即，令
$$a_{\delta }^{\ast }=\det {\left(x_j^{i-1}\right)}_{i,j=1}^n.$$
我们有 $a_{\delta }^{\ast }=(-1{)}^{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}{a}_{\delta }$ 因为矩阵 ${\left(x_j^{i-1}\right)}_{i,j=1}^n$ 是通过转置定义 $a_{\delta }$ 的矩阵然后反转行的顺序得到的。因此，(7.105) 右边的分子正好是 $a_{\delta }^{\ast }(q^{{\mu }_1},q^{{\mu }_2},\dots ,q^{{\mu }_n})$，其中 ${\mu }_j={\lambda }_j+n-j$，所以我们得到

$$s_{\lambda }(1,q,\dots ,q^{n-1})=(-1{)}^{\left(\genfrac{}{}{0ex}{}{n}{2}\right)}\prod _{1\le i<j\le n}\frac{q^{{\mu }_i}-q^{{\mu }_j}}{q^{i-1}-q^{j-1}}.\text{\hspace{1em}(7.106)}$$

由引理 7.21.1 可得（使用 ${\prod }_{1\le i<j\le n}[j-i]={\prod }_{i=1}^n[n-i]!$）
$$\begin{gathered} s_{\lambda }(1,q,\dots ,q^{n-1})=\frac{q^{{\sum }_{i<j}{\mu }_j}{\prod }_{i<j}[{\mu }_i-{\mu }_j]\cdot {\prod }_{i\ge 1}[{\mu }_i]!}{q^{{\sum }_{i<j}(j-1)}{\prod }_{i<j}[j-i]\cdot {\prod }_{i\ge 1}[{\mu }_i]!} \\ =q^{b(\lambda )}\prod _{u\in \lambda }\frac{[n+c(u)]}{[h(u)]}.∎ \end{gathered}$$

注意，
$$s_{\lambda }(1,q,\dots ,q^{n-1})=\sum _{\pi }{q}^{|\pi |},$$
其中 $\pi$ 遍历所有形状为 $\lambda$ 且最大部分不超过 $n-1$ 的列严格平面分拆 (= 反向 SSYT)，允许 0 作为部分。因此，定理 7.21.2 可被视为确定了这类平面分拆的生成函数，按它们的项和枚举。如果不希望 0 作为部分，那么 $s_{\lambda }$ 的齐次性给出
$$q^{|\lambda |}{s}_{\lambda }(1,q,\dots ,q^{n-1})=s_{\lambda }(q,q^2,\dots ,q^n)=\sum _{\pi }{q}^{|\pi |},$$
其中现在 $\pi$ 遍历所有形状为 $\lambda$ 且最大部分不超过 $n$ 的列严格平面分拆（通常条件是部分为正整数）。

如果现在我们在定理 7.21.2 中令 $n\to \infty$，那么分子 ${\prod }_{u\in \lambda }(1-q^{n+c(u)})$ 趋近于 1，因此我们得到稳定主特化 $s_{\lambda }(1,q,q^2,\dots )$ 的公式。

7.21.3 推论

对于任意 $\lambda \in \text{Par}$，我们有
$$s_{\lambda }(1,q,q^2,\dots )=\frac{q^{b(\lambda )}}{{\prod }_{u\in \lambda }[h(u)]}.$$

类似地，如果我们在定理 7.21.2 中设 $q=1$，那么我们得到（利用 $1-q^k=(1-q)(1+q+\cdots +q^{k-1})$ 这一事实，并从分子和分母中消去 $1-q$ 的因子）以下结果。（关于其表示论意义，请参见附录 2，方程 (A2.4) 及随后的讨论。）

7.21.4 推论

对于任意 $\lambda \in \text{Par}$ 和 $n\in \mathbb{P}$，我们有
$$s_{\lambda }(1^n)=\prod _{u\in \lambda }\frac{n+c(u)}{h(u)}.\text{\hspace{1em}(7.107)}$$

特别地，$s_{\lambda }(1^n)$ 的所有零点（视为 $n$ 的多项式）都是整数。

推论 7.21.3 有一些有趣的推论。例如，在命题 7.19.11 中设 $\mu =\varnothing$ 并与推论 7.21.3 比较，得到以下结果。

7.21.5 推论

对于任意 $\lambda \in \text{Par}$，我们有
$$\sum _T{q}^{\text{maj}(T)}=\frac{q^{b(\lambda )}[n!]}{{\prod }_{u\in \lambda }[h(u)]},$$
其中 $T$ 遍历形状为 $\lambda$ 的所有 SYT。

从推论 7.21.5 我们得到推论 7.16.3 之后提到的 $f^{\lambda }$ 的显式公式，从而也得到命题 7.10.3 中给出的组合对象的枚举。这个卓越的结果被称为钩长公式 (hook-length formula)。

7.21.6 推论

令 $\lambda ⊢n$。则
$$f^{\lambda }=\frac{n!}{{\prod }_{u\in \lambda }h(u)}.$$

证明. 在推论 7.21.5 中设 $q=1$。或者，由方程 (7.29) 我们可以将 $\lambda ⊢n$ 的推论 7.21.3 重述为
$$\exp (s_{\lambda })=\frac{t^n{q}^{b(\lambda )}}{{\prod }_{u\in \lambda }(1+q+\cdots +q^{h(u)-1})}.$$
现在令 $q=1$ 并使用命题 7.8.4(a) 给出的 ex 的解释。 ∎

我们可以将推论 7.21.3 和 7.21.5 都视为钩长公式的 $q$-模拟。推论 7.21.3 是对称函数 $q$-模拟，而推论 7.21.5 是组合 $q$-模拟。

定理 7.21.2 是列严格平面分拆的一个完全令人满意的生成函数，但它与普通平面分拆有什么关系呢？答案是对于矩形形状 $\lambda =⟨c^r⟩$，在形状为 $⟨c^r⟩$ 的列严格平面分拆和形状为 $⟨c^r⟩$ 的普通平面分拆之间存在一个简单的双射，并且这个双射对最大部分和项和的影响易于计算。这些断言将在以下定理的证明中解释，这是本节的主要结果。回想一下，$\pi \subseteq B(r,c,t)$ 意味着 $\pi$ 是一个图包含在盒子 $B(r,c,t)$ 中的平面分拆。

7.21.7 定理

固定 $r,c,t$ 且 $r\le c$。则
$$\begin{gathered} \sum _{\pi \subseteq B(r,c,t)}{q}^{|\pi |} \\ =\frac{[t+1][t+2{]}^2\cdots [t+r{]}^r[t+r+1{]}^r\cdots [t+c{]}^r[t+c+1{]}^{r-1}\cdots [t+c+r-1]}{[1][2{]}^2\cdots [r{]}^r[r+1{]}^r\cdots [c{]}^r[c+1{]}^{r-1}\cdots [c+r-1]}, \end{gathered}$$
(7.108)
其中 $[i]=1-q^i$.

证明. 令 $\lambda =⟨c^r⟩$，一个具有 $r$ 行和 $c$ 列的矩形形状。注意，假设 $r\le c$ 不失一般性，因为我们可以随时用 ${\lambda }^{\prime }$ 替换 $\lambda$。令 $\pi =({\pi }_{ij})$ 是一个形状为 $\lambda$ 的列严格平面分拆，允许 0 作为部分。通过 ${\pi }_{ij}^{\ast }={\pi }_{ij}-r+i$ 定义 ${\pi }^{\ast }=({\pi }_{ij}^{\ast })$。我们简单地将通常的将严格递减序列转换为弱递减序列的方法应用于 $\pi$ 的每一列。例如，如果
$$\pi =\begin{array}{cccccc}6& 6& 4& 4& 4& 3\\ 4& 3& 3& 2& 2& 1\\ 2& 2& 1& 1& 0& 0\end{array}$$
那么
$${\pi }^{\ast }=\begin{array}{cccccc}4& 4& 2& 2& 2& 1\\ 3& 2& 2& 1& 1& 0\\ 2& 2& 1& 1& 0& 0\end{array}.$$
显然 ${\pi }^{\ast }$ 是一个满足以下条件的平面分拆：
$${\ell }_1({\pi }^{\ast })\le r,{\ell }_2({\pi }^{\ast })\le c,$$
$$\max ({\pi }^{\ast })=\max (\pi )-r+1,|{\pi }^{\ast }|=|\pi |-\left(\genfrac{}{}{0ex}{}{r}{2}\right)c.$$
此外，给定这样一个平面分拆 ${\pi }^{\ast }$，我们可以通过 ${\pi }_{ij}={\pi }_{ij}^{\ast }+r-i$ 恢复 $\pi$。因此，我们从定理 7.21.2 得到
$$\sum _{\pi \subseteq B(r,c,t)}{q}^{|\pi |}=q^{-(j)c}{s}_{⟨c^r⟩}(1,q,\dots ,q^{t+r-1})$$
$$=q^{b(⟨c^r⟩)-(j)c}\prod _{u\in ⟨c^r⟩}\frac{[t+r+c(u)]}{[h(u)]}.\text{\hspace{1em}(7.109)}$$
注意 $b(⟨c^r⟩)=\left(\genfrac{}{}{0ex}{}{r}{2}\right)c$。此外，$⟨c^r⟩$ 的钩长多重集是 {1,22,33,…,rr,(r+1)r,…,cr,(c+1)r−1,(c+2)r−2,…,c+r−1}\{1, 2^2, 3^3, \ldots, r^r, (r+1)^r, \ldots, c^r, (c+1)^{r-1}, (c+2)^{r-2}, \ldots, c+r-1\}{1,22,33,…,rr,(r+1)r,…,cr,(c+1)r−1,(c+2)r−2,…,c+r−1}，而内容的多重集是通过从钩长中减去 $r$ 得到的。将这些 $c(u)$ 和 $h(u)$ 的值代入 (7.109) 就完成了证明。 ∎

读者可以检查，生成函数 (7.108) 的另一种写法更清楚地显示了 $r,c,$ 和 $t$ 之间的对称性（但它的分子和分母有 $rct$ 个因子而不是 $rc$ 个因子），由下式给出：
$$\sum _{\pi \subseteq B(r,c,t)}{q}^{|\pi |}=\prod _{i=1}^r\prod _{j=1}^c\prod _{k=1}^t\frac{[i+j+k-1]}{[i+j+k-2]}.\text{\hspace{1em}(7.110)}$$

定理 7.21.7 可以用第 3.15 节中发展的 $(P,\omega )$-分拆理论来解释。满足 ${\ell }_1(\pi )\le r,{\ell }_2(\pi )\le c,$ 和 $\max (\pi )\le t$ 的平面分拆 $\pi$ 可以被视为一个保序递减映射 $\pi :r\times c\to [0,t]$。换句话说，如果 $P$ 是偏序集 $r\times c$，那么 $\pi$ 正好是一个最大部分不超过 $t$ 的 $P$-分拆（即，一个 $(P,\omega )$-分拆，其中 $\omega$ 是自然标号）。因此，特别地，这种 $\pi$ 的数量正好是 ${\Omega }_P(t+1)$，其中 ${\Omega }_P$ 表示自然标号的序多项式（在第 3.15.4 节讨论过）。在 (7.108) 中设 $q=1$ 和 $t=m-1$ 得到

$${\Omega }_{r\times c}(m)$$

$$=\frac{m(m+1{)}^2\cdots (m+r-1{)}^r(m+r{)}^r\cdots (m+c-1{)}^r(m+c{)}^{r-1}\cdots (m+c+r-2)}{1\cdot 2^2\cdots r^r(r+1{)}^r\cdots c^r(c+1{)}^{r-1}\cdots (c+r-1)}.$$
特别地，$\Omega (r\times c,m)$ 的所有零点都是非正整数。此外，命题 3.5.1 的一个简单推广（见练习 3.171(a)）表明
$$\sum _{\pi \subseteq B(r,c,t)}{q}^{|\pi |}=\sum _{I\in J(r\times c\times t)}{q}^{\#I},\text{\hspace{1em}(7.111)}$$
即分配格 $J(r\times c\times t)$ 的秩生成函数。因此方程 (7.110) 等价于练习 3.170(b) 和 3.172(f)(i)。在 (7.111) 和 (7.110) 中设 $q=1$ 得到优雅的公式
$$\#J(r\times c\times t)=\prod _{i=1}^r\prod _{j=1}^c\prod _{k=1}^t\frac{i+j+k-1}{i+j+k-2}.$$