当前位置：首页 > news >正文

Leetcode+Java+动态规划II

news 2025/8/27 6:42:52

62.不同路径

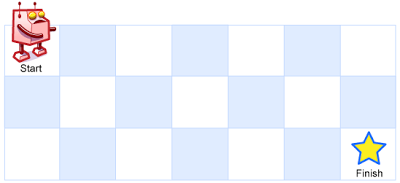
一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？
示例 1：
输入：m = 3, n = 7
输出：28
示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3：
输入：m = 7, n = 3
输出：28
示例 4：
输入：m = 3, n = 3
输出：6

原理

问题分解：
问题具有 重叠子问题 和 最优子结构：
重叠子问题：计算 dp[i] 需要 dp[i-1] 和 dp[i-2]，子问题会重复出现。
最优子结构：到达第 i 阶的最低花费可以由前两阶的最优解推导。
直接递归（如 min(climb(i-1) + cost[i-1], climb(i-2) + cost[i-2])）会导致重复计算，时间复杂度为 O(2^n)，对 cost.length ≤ 1000 会超时。
动态规划优化：
使用数组 dp 存储到达每阶楼梯的最低花费，dp[i] 表示到达第 i 阶的最低花费。
初始化：
dp[0] = 0：从第 0 阶开始，无需支付费用。
dp[1] = 0：从第 1 阶开始，无需支付费用。
状态转移：
对于 i ≥ 2，dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i-1])。
表示从 i-2 阶爬 2 步或从 i-1 阶爬 1 步，选择花费较小的路径。
迭代从 i = 2 到 cost.length，填充 dp 数组，最终 dp[cost.length] 是到达楼顶的最低花费。
边界处理：
dp[0] = 0, dp[1] = 0 直接处理了从下标 0 或 1 开始的情况。
循环从 i = 2 开始，确保不访问无效索引（如 cost[-1]）。
时间和空间复杂度：
时间复杂度：O(n)，其中 n = cost.length，循环从 i = 2 到 n，执行 n-1 次迭代，每次操作是 O(1)。
空间复杂度：O(n)，使用大小为 n+1 的 dp 数组。

代码

class Solution {public int minCostClimbingStairs(int[] cost) {// 创建 DP 数组，dp[i] 表示到达第 i 阶楼梯的最低花费// 数组大小为 cost.length + 1，因为楼顶是第 cost.length 阶int[] dp = new int[cost.length + 1];// 初始化：从下标 0 或 1 开始，无需支付费用dp[0] = 0; // 到达第 0 阶的花费为 0（起点）dp[1] = 0; // 到达第 1 阶的花费为 0（起点）// 从第 2 阶开始，计算到达每阶的最低花费// 状态转移：dp[i] = min(dp[i-2] + cost[i-2], dp[i-1] + cost[i-1])// 即从 i-2 阶爬 2 步（支付 cost[i-2]）或从 i-1 阶爬 1 步（支付 cost[i-1]）for (int i = 2; i <= cost.length; i++) {dp[i] = Math.min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);}// 返回到达楼顶（第 cost.length 阶）的最低花费return dp[cost.length];}
}

63.不同路径II

给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。
网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含任何有障碍物的方格。
返回机器人能够到达右下角的不同路径数量。
测试用例保证答案小于等于 2 * 109。
示例 1：
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2：
输入：obstacleGrid = [[0,1],[0,0]]
输出：1
提示：
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

原理

问题分解：
到达格子 (i,j) 的路径数量取决于：
从上方 (i-1,j) 向下移动，路径数为 dp[i-1][j]。
从左方 (i,j-1) 向右移动，路径数为 dp[i][j-1]。
状态转移方程：
如果 obstacleGrid[i][j] == 1，dp[i][j] = 0（障碍物，路径数为 0）。
否则，dp[i][j] = dp[i-1][j] + dp[i][j-1]。
问题具有 重叠子问题 和 最优子结构：
重叠子问题：计算 dp[i][j] 需要 dp[i-1][j] 和 dp[i][j-1]，子问题重复出现。
最优子结构：路径总数由上方和左方的路径总数直接推导。
初始化：
第一行和第一列的路径数：
如果没有障碍物，dp[i][0] = 1（只能向下），dp[0][j] = 1（只能向右）。
如果遇到障碍物，后续格子路径数为 0。
如果起点 (0,0) 有障碍物，dp[0][0] = 0。
动态规划优化：
使用二维数组 dp[i][j] 存储到达 (i,j) 的路径数量。
迭代填充 dp 数组，从 (1,1) 到 (m-1,n-1)。
最终 dp[m-1][n-1] 是答案。
时间和空间复杂度：
时间复杂度：O(m * n)，需要填充 m * n 的 DP 数组，每个格子计算是 O(1)。
空间复杂度：O(m * n)，使用二维 DP 数组。

代码

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;if (obstacleGrid[0][0] == 1) return 0;int[] dp = new int[n];dp[0] = 1; // 起点路径数为 1// 初始化第一行for (int j = 1; j < n; j++) {dp[j] = (obstacleGrid[0][j] == 1 || dp[j-1] == 0) ? 0 : 1;}// 填充 DP 数组for (int i = 1; i < m; i++) {// 更新第一列dp[0] = (obstacleGrid[i][0] == 1 || dp[0] == 0) ? 0 : 1;for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) {dp[j] = 0;} else {dp[j] = dp[j] + dp[j-1]; // dp[j] 表示上一行的 dp[i-1][j]}}}return dp[n-1];}
}

343.整数拆分

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58

原理

问题分解：
给定整数 n，需要将其拆分为至少两个正整数（如 n = j + (i-j)），并最大化乘积。
问题具有 重叠子问题 和 最优子结构：
重叠子问题：拆分 n 时，可能需要计算子问题（如 n-j 的最大乘积）。
最优子结构：n 的最大乘积可以通过拆分为 j 和 (n-j)，并结合 (n-j) 的最大乘积来推导。
直接枚举所有拆分方式（例如递归）会导致指数时间复杂度，不适合 n ≤ 58。
动态规划定义：
定义 dp[i] 为将正整数 i 拆分为至少两个正整数后的最大乘积。
初始化：
dp[2] = 1：2 = 1 + 1，乘积为 1 * 1 = 1。
对于 i < 2，无需初始化，因为题目要求至少拆分为两个数，i=1 无意义。
状态转移：
对于每个 i（从 3 到 n），尝试将其拆分为 j 和 (i-j)，其中 j 从 1 到 i/2（因为 j 和 i-j 对称，j > i/2 会重复）。
对于每种拆分：
直接相乘：j * (i-j)。
进一步拆分 (i-j)：j * dp[i-j]。
取两者的最大值，并与当前 dp[i] 比较：dp[i] = max(dp[i], max(j * (i-j), j * dp[i-j]))。
最终 dp[n] 是答案。
为什么循环到 i/2：
当拆分 i = j + (i-j) 时，j 和 i-j 的乘积是对称的。例如，j=1, i-j=5 和 j=5, i-j=1 的乘积相同。
因此，只需遍历 j 到 i/2 即可，避免重复计算。
时间和空间复杂度：
时间复杂度：O(n^2)，外层循环 i 从 3 到 n（O(n)），内层循环 j 从 1 到 i/2（平均 O(n/2)）。
空间复杂度：O(n)，使用大小为 n+1 的 dp 数组。

代码

import java.util.*;class Solution {public int integerBreak(int n) {// 创建 DP 数组，dp[i] 表示将正整数 i 拆分为至少两个正整数后的最大乘积int[] dp = new int[n + 1];// 初始化：n=2 时，拆分为 1+1，乘积为 1dp[2] = 1;// 从 i=3 开始，计算将 i 拆分后的最大乘积for (int i = 3; i <= n; i++) {// 尝试将 i 拆分为 j 和 (i-j)，其中 j 从 1 到 i/2for (int j = 1; j <= i / 2; j++) {// dp[i] 取以下三者的最大值：// 1. 当前 dp[i]（保持不变）// 2. 直接相乘：j * (i-j)// 3. 拆分 (i-j) 后再乘 j：dp[i-j] * jdp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));}}// 返回将 n 拆分后的最大乘积return dp[n];}
}

96.不同的二叉搜索树

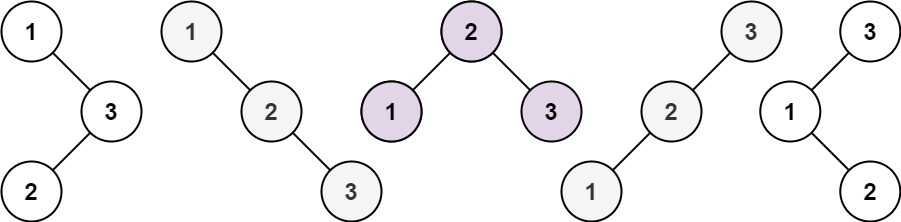
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
示例 1：
输入：n = 3
输出：5
示例 2：
输入：n = 1
输出：1
提示：
1 <= n <= 19

原理

问题分解：
假设有 i 个节点（值从 1 到 i），选择某个节点 k 作为根：
左子树包含 k-1 个节点（值 1 到 k-1），方案数为 dp[k-1]。
右子树包含 i-k 个节点（值 k+1 到 i），方案数为 dp[i-k]。
以 k 为根的 BST 种数为 dp[k-1] * dp[i-k]。
对所有可能的根节点 k（从 1 到 i）求和：dp[i] = Σ(dp[j] * dp[i-1-j])，其中 j 从 0 到 i-1。
这与卡塔兰数公式一致：C(n) = Σ(C(j) * C(n-1-j))，j 从 0 到 n-1。
初始化：
dp[0] = 1：0 个节点只有 1 种方案（空树）。
dp[1] = 1：1 个节点只有 1 种方案（单节点树）。
dp[2] = 2：2 个节点有 2 种方案（左子树或右子树为空）。
状态转移：
对于 i（从 3 到 n），dp[i] = Σ(dp[j] * dp[i-1-j])，j 从 0 到 i-1。
每个 dp[i] 表示 i 个节点的所有可能 BST 种数。
时间和空间复杂度：
时间复杂度：O(n^2)，外层循环 i 从 3 到 n，内层循环 j 从 0 到 i-1。
空间复杂度：O(n)，使用大小为 n+1 的 dp 数组。

代码

import java.util.*;class Solution {public int numTrees(int n) {// 创建 DP 数组，dp[i] 表示 i 个节点组成的 BST 种数int[] dp = new int[n + 1];// 初始化dp[0] = 1; // 0 个节点，1 种方案（空树）dp[1] = 1; // 1 个节点，1 种方案// 从 i=2 开始，计算 i 个节点的 BST 种数for (int i = 2; i <= n; i++) {// 遍历左子树节点数 j（从 0 到 i-1）for (int j = 0; j < i; j++) {// 左子树 j 个节点，右子树 i-1-j 个节点dp[i] += dp[j] * dp[i - 1 - j];}}// 返回 n 个节点的 BST 种数return dp[n];}
}

查看全文

http://www.dtcms.com/a/351514.html