强化学习基础总结
文章目录
- 强化学习
- 1 基本概念
- 2 贝尔曼公式(Bellman equation)
- 3 贝尔曼最优公式(Bellman optimality equation)
- 4 迭代算法
- Value iteration
- Policy iteration
- Truncated policy iteration
- 5 蒙特卡洛方法(Model free)
- 6 随机近似理论与随机梯度下降
- 7 时序差分方法(Temporal-Difference)
- 8 值函数近似
- state value
- action value
- DQN
- 9 策略梯度方法
- metrics to define optimal policies
- Gradients of the metrics
- Gradient-ascent
- 10 Actor-Critic方法
强化学习
1 基本概念
-
State:agent相对于环境的状态,s1,s2,...s9s_1,s_2,...s_9s1,s2,...s9
-
State space:state的集合
-
Action:每个状态的可能行为,A(s)A(s)A(s)
-
State transition:状态转移,p(s2∣s1,a)p(s_2|s_1,a)p(s2∣s1,a)
-
Policy:告诉智能体在某个状态应该采取哪个行动,用π条件概率表示。
- π(a1∣s1)=kπ(a_1|s_1)=kπ(a1∣s1)=k表示在状态s1采取a1行动的概率
-
Reward:正数为奖励,负数为惩罚,集合为R(s,a)R(s,a)R(s,a),概率为p(r,∣s,a)p(r,|s,a)p(r,∣s,a)
-
Trajectory:state-action-reward链
-
Return:基于一个Trajectory得到的reward之和
-
Discounted return:加一个discount rate γ∈[0,1)γ∈[0,1)γ∈[0,1),防止return加到无穷,值越小越注重近处的reward
-
Episode和continuing tasks:前者表示到target state后就不动了,后者会继续。实际中会将target state看做普通state,可能会跳出target,就将episode转换成continuing tasks。
2 贝尔曼公式(Bellman equation)
- State value:从一个状态出发得到的平均return,就是discounted return的期望,多个Trajectory得到的return和的平均值
vπ(s)=E[Gt∣St=s]v_\pi(s)=\mathbb{E}[G_t|S_t=s] vπ(s)=E[Gt∣St=s]
- Bellman equation:
vπ(s)=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=∑aπ(a∣s)∑rp(r∣s,a)r+γ∑aπ(a∣s)∑s′p(s′∣s,a)vπ(s′)=∑aπ(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)vπ(s′)]\begin{aligned} v_\pi(s)&=\mathbb{E}[R_{t+1}|S_t=s]+\gamma\mathbb{E}[G_{t+1}|S_t=s] \\ &=\sum_a\pi(a|s)\sum_rp(r|s,a)r+\gamma\sum_a\pi(a|s)\sum_{s'}p(s'|s,a)v_\pi(s') \\ &=\sum_a\pi(a|s)[\sum_rp(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v_\pi(s')] \end{aligned} vπ(s)=E[Rt+1∣St=s]+γE[Gt+1∣St=s]=a∑π(a∣s)r∑p(r∣s,a)r+γa∑π(a∣s)s′∑p(s′∣s,a)vπ(s′)=a∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπ(s′)]
- 矩阵形式
vπ=rπ+γPπvπv_\pi=r_\pi+\gamma P_\pi v_\pi vπ=rπ+γPπvπ
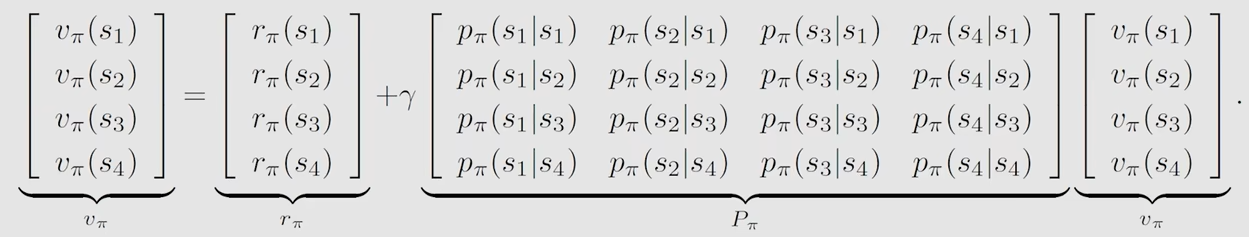
- 求解
vk+1=rπ+γPπvkv_{k+1}=r_\pi+\gamma P_\pi v_k vk+1=rπ+γPπvk
- Action value:从一个状态出发并选择一个Action的平均return
qπ(a,s)=E[Gt∣St=s,At=a]q_\pi(a,s)=\mathbb{E}[G_t|S_t=s,A_t=a] qπ(a,s)=E[Gt∣St=s,At=a]vπ(s)=∑aπ(a∣s)qπ(a,s)v_\pi(s)=\sum_a\pi(a|s)q_\pi(a,s) vπ(s)=a∑π(a∣s)qπ(a,s)
3 贝尔曼最优公式(Bellman optimality equation)
- Bellman optimality equation
v(s)=maxπ∑aπ(a∣s)[∑rp(r∣s,a)r+γ∑s′p(s′∣s,a)v(s′)]=maxπ∑aπ(a∣s)q(a,s)\begin{aligned} v(s)&=\underset{\pi}{max}\sum_a\pi(a|s)[\sum_rp(r|s,a)r+\gamma\sum_{s'}p(s'|s,a)v(s')]\\ &=\underset{\pi}{max}\sum_a\pi(a|s)q(a,s) \end{aligned} v(s)=πmaxa∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)v(s′)]=πmaxa∑π(a∣s)q(a,s)v=f(v)=maxπ(rπ+γPπv)v=f(v)=\underset{\pi}{max}(r_\pi+\gamma P_\pi v) v=f(v)=πmax(rπ+γPπv)
- 求解:
maxπ∑aπ(a∣s)q(s,a)=maxa∈A(s)q(s,a)π(a∣s)={1a=a∗0a≠a∗a∗=argmaxaq(a,s)\begin{aligned} \underset{\pi}{max}\sum_a\pi(a|s)q(s,a)=\underset{a∈A(s)}{max}q(s,a)\\ \pi(a|s)= \begin{cases} 1 & a=a^* \\ 0 & a\neq a^* \end{cases}\\ a^*=arg max_aq(a,s) \end{aligned} πmaxa∑π(a∣s)q(s,a)=a∈A(s)maxq(s,a)π(a∣s)={10a=a∗a=a∗a∗=argmaxaq(a,s)
4 迭代算法
Value iteration
vk+1=f(vk)=maxπ(rπ+γPπvk)v_{k+1}=f(v_k)=\underset{\pi}{max}(r_\pi+\gamma P_\pi v_k) vk+1=f(vk)=πmax(rπ+γPπvk)
- policy update
已知v带入算策略π
πk+1=argmaxπ(rπ+γPπvk)\pi_{k+1}=arg\underset{\pi}{max}(r_\pi+\gamma P_\pi v_k) πk+1=argπmax(rπ+γPπvk)
- value update
得到的π带入计算下一个v,这里的v不是贝尔曼解
vk+1=rπk+1+γPπk+1vkv_{k+1}=r_{\pi_{k+1}}+\gamma P_{\pi_{k+1}} v_k vk+1=rπk+1+γPπk+1vk
Policy iteration
- policy evaluation
已知策略π,循环迭代j趋于无穷大时算出最优的v
vπk(j+1)=rπk+γPπkvπk(j)v_{\pi k}^{(j+1)}=r_{\pi_{k}}+\gamma P_{\pi_{k}} v_{\pi k}^{(j)} vπk(j+1)=rπk+γPπkvπk(j)
- policy improvement
得到的v再计算新的策略π
πk+1=argmaxπ(rπ+γPπvπk)\pi_{k+1}=arg\underset{\pi}{max}(r_\pi+\gamma P_\pi v_{\pi k}) πk+1=argπmax(rπ+γPπvπk)
靠近目标状态的地方先到达最优策略
Truncated policy iteration
与policy iteration相比j不需要趋于无穷大,只要达到一个阈值即可
5 蒙特卡洛方法(Model free)
平均数近似期望
- MC Basic
就是Policy iteration在policy evaluation计算Action value 即q(a,s)时,采样大量return数据求平均作为q的期望,然后选最大的q的策略,与原Policy iteration相比不需要先计算state value(v)
使用Initial-visit method,在episode中访问一个s、a时,剩下的来估计这个s、a的Action value
- MC Exploring Starts
提高计算效率,在episode中从后往前计算q
-
MC without exploring start
- εεε-greedy policy:非确定性策略
π(a∣s)={1−ε∣A(s)∣(∣A(s)∣−1)greedyaction(qπ∗(s,a)ε∣A(s)∣others\pi(a|s)= \begin{cases} 1-\frac{ε}{|A(s)|}(|A(s)|-1) & greedy\ action(q_{\pi}^*(s,a) \\ \frac{ε}{|A(s)|}&others \end{cases} π(a∣s)={1−∣A(s)∣ε(∣A(s)∣−1)∣A(s)∣εgreedy action(qπ∗(s,a)others
|A(s)|是action的个数
- MC Epsilon-Greedy
策略集合使用ε-greedy policy,具有一定的探索性,ε越接近1探索性越强
6 随机近似理论与随机梯度下降
- 求平均数的迭代算法
wk+1=1k∑i=1kxiwk=1k−1∑i=1k−1xiwk+1=wk−1k(wk−xk)\begin{aligned} w_{k+1}&=\frac{1}{k}\sum_{i=1}^kx_i \\ w_{k}&=\frac{1}{k-1}\sum_{i=1}^{k-1}x_i \\ w_{k+1}&=w_k-\frac{1}{k}(w_k-x_k) \end{aligned} wk+1wkwk+1=k1i=1∑kxi=k−11i=1∑k−1xi=wk−k1(wk−xk)
-
Stochastic approximation(随机近似):使用随机+迭代的算法解决求解方程或优化问题,不需知道方程表达式。
- Robbins-Monro算法:求g(w)=0g(w)=0g(w)=0的问题,
wk+1=wk−αkg~(wk,ηk)g~(wk,ηk)=g(wk)+ηk\begin{aligned} w_{k+1}&=w_k-\alpha_k \tilde{g}(w_k,\eta_k)\\ \tilde{g}(w_k,\eta_k)&=g(w_k)+\eta_k \end{aligned} wk+1g~(wk,ηk)=wk−αkg~(wk,ηk)=g(wk)+ηk
收敛条件:
{0<c1≤∇wg(w)≤c2g(w)必须递增,相当于凸函数的梯度是g(w)∑k=1∞ak=∞and∑k=1∞ak2<∞表示ak收敛于0但不要太快E[ηk∣Hk]=0andE[ηk2∣Hk]<∞噪声的均值是0方差有限\begin{cases} 0<c_1\le\nabla_wg(w)\le c2 &g(w)必须递增,相当于凸函数的梯度是g(w)\\ \sum_{k=1}^\infty a_k=\infty \ and\sum_{k=1}^\infty a_k^2<\infty\ &表示a_k收敛于0但不要太快\\ \mathbb{E}[\eta_k|H_k]=0\ and\ \mathbb{E}[\eta_k^2|H_k]<\infty&噪声的均值是0方差有限 \end{cases} ⎩⎨⎧0<c1≤∇wg(w)≤c2∑k=1∞ak=∞ and∑k=1∞ak2<∞ E[ηk∣Hk]=0 and E[ηk2∣Hk]<∞g(w)必须递增,相当于凸函数的梯度是g(w)表示ak收敛于0但不要太快噪声的均值是0方差有限
-
梯度下降
-
梯度下降GD:
wk+1=wk−αk∇wE[f(wk,X)]=wk−αkE[∇wf(wk,X)]w_{k+1}=w_k-\alpha_k\nabla_w\mathbb{E}[f(w_k,X)]=w_k-\alpha_k\mathbb{E}[\nabla_wf(w_k,X)] wk+1=wk−αk∇wE[f(wk,X)]=wk−αkE[∇wf(wk,X)]
-
批量梯度下降BGD(无模型时平均代替期望):
E[∇wf(wk,X)]≈1n∑i=1n∇wf(wk,xi)\mathbb{E}[\nabla_wf(w_k,X)]\approx \frac{1}{n}\sum_{i=1}^n\nabla_wf(w_k,x_i) E[∇wf(wk,X)]≈n1i=1∑n∇wf(wk,xi)
-
随机梯度下降SGD:
wk+1=wk−αk∇wf(wk,xk)w_{k+1}=w_k-\alpha_k\nabla_wf(w_k,x_k) wk+1=wk−αk∇wf(wk,xk)
-
7 时序差分方法(Temporal-Difference)
- 求state value的TD算法
{vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]]s=stvt+1(s)=vt(s)s≠st\begin{cases} v_{t+1}(s_t)=v_t(s_t)-\alpha_t(s_t)[v_t(s_t)-[r_{t+1}+\gamma v_t(s_{t+1})]]&s=s_t \\ v_{t+1}(s)=v_t(s)&s\neq s_t \end{cases} {vt+1(st)=vt(st)−αt(st)[vt(st)−[rt+1+γvt(st+1)]]vt+1(s)=vt(s)s=sts=st
-
求action value的TD算法
- Sarsa (st,at,rt+1,st+1,at+1)(s_t,a_t,r_{t+1},s_{t+1},a_{t+1})(st,at,rt+1,st+1,at+1)
{qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]](s,a)=(st,at)qt+1(s,a)=qt(s,a)(s,a)≠(st,at)\begin{cases} q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma q_t(s_{t+1},a_{t+1})]]&(s,a)= (s_t,a_t) \\ q_{t+1}(s,a)=q_t(s,a)&(s,a)\neq (s_t,a_t) \end{cases} {qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γqt(st+1,at+1)]]qt+1(s,a)=qt(s,a)(s,a)=(st,at)(s,a)=(st,at)
Expected Sarsa
{qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γE[qt(st+1,A)]](s,a)=(st,at)qt+1(s,a)=qt(s,a)(s,a)≠(st,at)\begin{cases} q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma \mathbb{E}[q_t(s_{t+1},A)]]&(s,a)= (s_t,a_t) \\ q_{t+1}(s,a)=q_t(s,a)&(s,a)\neq (s_t,a_t) \end{cases} {qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γE[qt(st+1,A)]]qt+1(s,a)=qt(s,a)(s,a)=(st,at)(s,a)=(st,at)E[qt(st+1,A])]=∑aπt(a∣st+1)qt(st+1,a)=vt(st+1)\mathbb{E}[q_t(s_{t+1},A])]=\sum_a\pi_t(a|s_{t+1})q_t(s_{t+1},a)=v_t(s_{t+1}) E[qt(st+1,A])]=a∑πt(a∣st+1)qt(st+1,a)=vt(st+1)

上图为MC、Sarsa和n-step Sarsa方法的对比,主要是action value计算展开的个数不同
蒙特卡洛方法需要等所有时刻的采样值得到才可以更新(offline),Sarsa方法得到一次就可以(online),n-step的话属于折中。
只求解贝尔曼方程,不能直接估计出最优策略
- Q-learning
{qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γmaxa∈Aqt(st+1,a)]](s,a)=(st,at)qt+1(s,a)=qt(s,a)(s,a)≠(st,at)\begin{cases} q_{t+1}(s_t,a_t)=q_t(s_t,a_t)-\alpha_t(s_t,a_t)[q_t(s_t,a_t)-[r_{t+1}+\gamma\ \underset{a∈A}{max}\ q_t(s_{t+1},a)]]&(s,a)= (s_t,a_t) \\ q_{t+1}(s,a)=q_t(s,a)&(s,a)\neq (s_t,a_t) \end{cases} {qt+1(st,at)=qt(st,at)−αt(st,at)[qt(st,at)−[rt+1+γ a∈Amax qt(st+1,a)]]qt+1(s,a)=qt(s,a)(s,a)=(st,at)(s,a)=(st,at)
用来求解贝尔曼最优公式,使用(st,at,rt+1,st+1)(s_t,a_t,r_{t+1},s_{t+1})(st,at,rt+1,st+1)
-
on-policy和off-policy,前者behavior策略和target策略相同,后者不同。
-
behavior策略:与环境交互生成experience
-
target策略:最终更新得到的最优策略
-
Sarsa:(st,at)(s_t,a_t)(st,at)给定,rt+1r_{t+1}rt+1和st+1s_{t+1}st+1不依赖于策略,而是模型的概率,而at+1a_{t+1}at+1是在st+1s_{t+1}st+1状态下根据πt(st+1)\pi_t(s_{t+1})πt(st+1)策略生成并采样得到的,所以πt\pi_tπt是behavior策略,根据πtπ_tπt得到action value,再用action value更新πtπ_tπt得到πt+1π_{t+1}πt+1,所以所以πt\pi_tπt也是target策略,所以Sarsa是on-policy
-
MC也是on-policy的,与Sarsa类似
-
Q-learning,它的behavior策略是从sts_tst出发根据一个策略πb\pi_bπb得到ata_tat,而target策略是找到计算得到的q最大的action对应的策略作为target策略πa\pi_aπa时,πb\pi_bπb不会更新只用来生成数据,二者不一样所以是off-policy。当更新target策略使用ε-greedy,πb\pi_bπb既要生成数据,又要被更新,所以是on-policy。理解为策略πb\pi_bπb用来探索,找出最优πa\pi_aπa
-
8 值函数近似
state value
使用函数来拟合原来的state value,离散变连续:vπ(s)→v^(s,w)v_\pi(s)\rightarrow\hat{v}(s,w)vπ(s)→v^(s,w)
object function:J(w)=E[(vπ(S)−v^(S,w))2]J(w)=\mathbb{E}[(v_\pi(S)-\hat{v}(S,w))^2]J(w)=E[(vπ(S)−v^(S,w))2],平稳分布来求E
随机梯度下降法优化:
wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t(v_\pi(s_t)-\hat{v}(s_t,w_t))\nabla_w\hat{v}(s_t,w_t) wt+1=wt+αt(vπ(st)−v^(st,wt))∇wv^(st,wt)
由于不知道vπ(st)v_\pi(s_t)vπ(st),使用MC和TD方法来解决:
-
MC:wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t(g_t-\hat{v}(s_t,w_t))\nabla_w\hat{v}(s_t,w_t)wt+1=wt+αt(gt−v^(st,wt))∇wv^(st,wt),gt是从一个状态沿episode出发得到的Discounted return。
-
TD:wt+1=wt+αt(rt+1+γv^(st+1,wt)−v^(st,wt))∇wv^(st,wt)w_{t+1}=w_t+\alpha_t(r_{t+1}+\gamma\hat{v}(s_{t+1},w_t)-\hat{v}(s_t,w_t))\nabla_w\hat{v}(s_t,w_t)wt+1=wt+αt(rt+1+γv^(st+1,wt)−v^(st,wt))∇wv^(st,wt)
当使用线性函数来拟合时,可以写成:v^(s,w)=ϕT(s)w\hat{v}(s,w)=\phi^T(s)wv^(s,w)=ϕT(s)w
- TD_linear:wt+1=wt+αt(rt+1+γϕT(st+1)wt−ϕT(st)wt)ϕ(st)w_{t+1}=w_t+\alpha_t(r_{t+1}+\gamma\phi^T(s_{t+1})w_t-\phi^T(s_{t})w_t)\phi(s_t)wt+1=wt+αt(rt+1+γϕT(st+1)wt−ϕT(st)wt)ϕ(st)
action value
- sarsa:
在policy evaluation阶段计算的是wt+1w_{t+1}wt+1而不是直接计算qt+1q_{t+1}qt+1,带入到q^(s,a,w)\hat{q}(s,a,w)q^(s,a,w)得到q,再进入policy improvement阶段。
wt+1=wt+αt(rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt))∇wq^(st,at,wt)w_{t+1}=w_t+\alpha_t(r_{t+1}+\gamma\hat{q}(s_{t+1},a_{t+1},w_t)-\hat{q}(s_t,a_t,w_t))\nabla_w\hat{q}(s_t,a_t,w_t)wt+1=wt+αt(rt+1+γq^(st+1,at+1,wt)−q^(st,at,wt))∇wq^(st,at,wt)
- q-learning:
wt+1=wt+αt(rt+1+γmaxa∈A(st+1)q^(st+1,a,wt)−q^(st,at,wt))∇wq^(st,at,wt)w_{t+1}=w_t+\alpha_t(r_{t+1}+\gamma \underset{a∈A(s_{t+1})}{max} \hat{q}(s_{t+1},a,w_t)-\hat{q}(s_t,a_t,w_t))\nabla_w\hat{q}(s_t,a_t,w_t) wt+1=wt+αt(rt+1+γa∈A(st+1)maxq^(st+1,a,wt)−q^(st,at,wt))∇wq^(st,at,wt)
DQN
object function:J(w)=E[R+γmaxa∈A(S′)q^(S′,a,wT)−q^(S,A,w))2]J(w)=\mathbb{E}[R+\gamma \underset{a∈A(S')}{max}\hat q(S',a,w_T)-\hat{q}(S,A,w))^2]J(w)=E[R+γa∈A(S′)maxq^(S′,a,wT)−q^(S,A,w))2]
定义了两个网络main network和target network,参数分别为w和wtw_twt,在求梯度时将target中的w看做常数wTw_TwT,w不断优化,wTw_TwT隔段时间将w的值赋过来。

9 策略梯度方法
函数表示策略:π(a∣s,θ)\pi(a|s,\theta)π(a∣s,θ)
metrics to define optimal policies
- average value:
vπ−=∑s∈Sd(s)vπ(s)=E[vπ(S)]=dTvπ=E[∑t=0∞γtRt+1]\overset{-}{v_\pi}=\sum_{s∈\mathcal{S}}d(s)v_\pi(s)=\mathbb{E}[v_\pi(S)]=d^Tv_\pi=\mathbb{E}[\sum_{t=0}^\infty\gamma^tR_{t+1}] vπ−=s∈S∑d(s)vπ(s)=E[vπ(S)]=dTvπ=E[t=0∑∞γtRt+1]
-
d与π\piπ没有关系,写成d0,可以是状态个数分之一,一视同仁,也可以是关注某个状态令其d0等于1其余等于0
-
与π\piπ有关,写成dπ(s)d_\pi(s)dπ(s)
- average reward:
rπ−=∑s∈Sdπ(s)rπ(s)=E[rπ(S)]=limn→∞1nE[∑k=1nRt+k]rπ(s)=.∑a∈Aπ(a∣s)r(s,a)r(s,a)=E[R∣s,a]=∑rp(r∣s,a)\begin{aligned} \overset{-}{r_\pi}&=\sum_{s∈\mathcal{S}}d_\pi(s)r_\pi(s)=\mathbb{E}[r_\pi(S)]=\underset{n\rightarrow\infty}{lim}\frac{1}{n}\mathbb{E}[\sum_{k=1}^nR_{t+k}]\\ r_\pi(s)&\overset{.}{=}\sum_{a∈\mathcal{A}}\pi(a|s)r(s,a)\\ r(s,a)&=\mathbb{E}[R|s,a]=\sum_rp(r|s,a) \end{aligned} rπ−rπ(s)r(s,a)=s∈S∑dπ(s)rπ(s)=E[rπ(S)]=n→∞limn1E[k=1∑nRt+k]=.a∈A∑π(a∣s)r(s,a)=E[R∣s,a]=r∑p(r∣s,a)
Gradients of the metrics
∇θJ(θ)=∑s∈Sη(s)∑a∈A∇θπ(a∣s,θ)qπ(s,a)=ES∈η,A∈π[∇θlnπ(A∣S,θ)qπ(S,A)]\begin{aligned} \nabla_\theta J(\theta)&=\sum_{s∈\mathcal{S}}\eta(s)\sum_{a∈\mathcal A}\nabla_\theta\pi(a|s,\theta)q_\pi(s,a) \\&=\mathbb{E}_{S∈\eta,A∈\pi}[\nabla_\theta ln\pi(A|S,\theta)q_\pi(S,A)] \end{aligned} ∇θJ(θ)=s∈S∑η(s)a∈A∑∇θπ(a∣s,θ)qπ(s,a)=ES∈η,A∈π[∇θlnπ(A∣S,θ)qπ(S,A)]
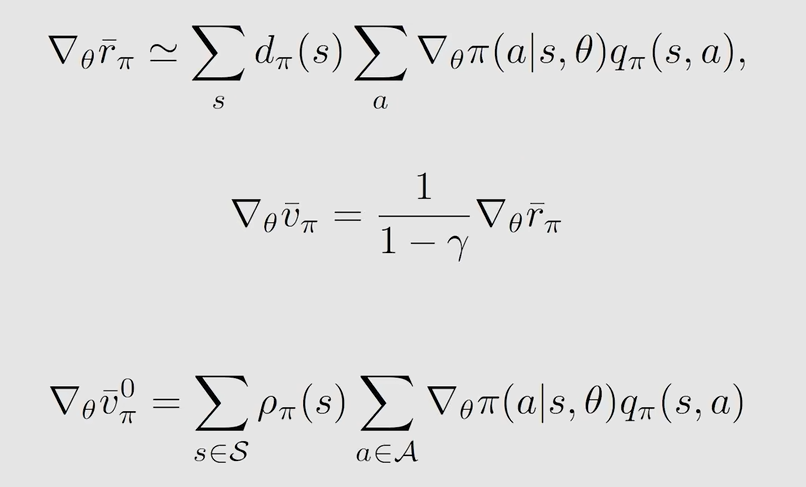
Gradient-ascent
θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)=θt+α(qt(st,at)π(at∣st,θt))∇θπ(at∣st,θt)\begin{aligned} \theta_{t+1}&=\theta_t+\alpha\nabla_\theta ln\pi(a_t|s_t,\theta_t)q_t(s_t,a_t) \\&=\theta_t+\alpha(\frac{q_t(s_t,a_t)}{\pi(a_t|s_t,\theta_t)})\nabla_\theta \pi(a_t|s_t,\theta_t) \end{aligned} θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)=θt+α(π(at∣st,θt)qt(st,at))∇θπ(at∣st,θt)
-
qt(st,at)q_t(s_t,a_t)qt(st,at)较大时,说明前一个策略的action value大,充分利用前面的策略(exploitation)
-
π(at∣st,θt)\pi(a_t|s_t,\theta_t)π(at∣st,θt)较小时,说明前一个策略选择at的概率小的话,下一次会选择更大的概率(exploration)
qtq_tqt通过蒙特卡洛方法给定一个episode返回的return,这样的话就是reinforce。

10 Actor-Critic方法
- Actor:生成策略的过程。
θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)\theta_{t+1}=\theta_t+\alpha\nabla_\theta ln\pi(a_t|s_t,\theta_t)q_t(s_t,a_t) θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)
- Critic:评估策略的action value或state value,估计qtq_tqt
- QAC:Critic使用Sarsa+值函数估计,Actor使用前面的梯度上升的策略更新算法

- Advantage actor-critic(A2C)
θt+1=θt+αE[∇θlnπ(A∣S,θt)[qπ(S,A)−vπ(S)]]=θt+αE[∇θlnπ(A∣S,θt)δπ(S,A)]θt+1=θt+α∇θlnπ(at∣st,θt)[qt(st,at)−vt(st)]=θt+α∇θlnπ(at∣st,θt)[δt(st,at)]\begin{aligned} \theta_{t+1}&=\theta_t+\alpha\mathbb{E}[\nabla_\theta ln\pi(A|S,\theta_t)[q_\pi(S,A)-v_\pi(S)]] \\&=\theta_t+\alpha\mathbb{E}[\nabla_\theta ln\pi(A|S,\theta_t)\delta_\pi(S,A)] \\\theta_{t+1}&=\theta_t+\alpha\nabla_\theta ln\pi(a_t|s_t,\theta_t)[q_t(s_t,a_t)-v_t(s_t)] \\&=\theta_t+\alpha\nabla_\theta ln\pi(a_t|s_t,\theta_t)[\delta_t(s_t,a_t)] \end{aligned} θt+1θt+1=θt+αE[∇θlnπ(A∣S,θt)[qπ(S,A)−vπ(S)]]=θt+αE[∇θlnπ(A∣S,θt)δπ(S,A)]=θt+α∇θlnπ(at∣st,θt)[qt(st,at)−vt(st)]=θt+α∇θlnπ(at∣st,θt)[δt(st,at)]
减小方差

- 重要性采样
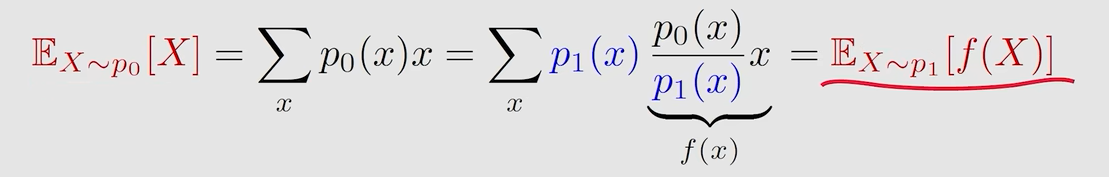
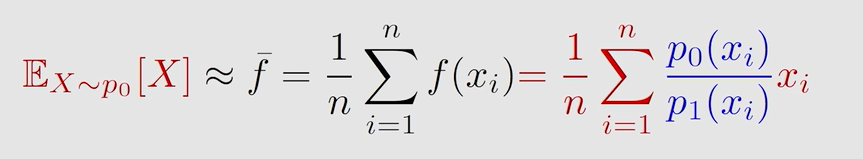
将on-policy转成off-policy,使用重要性采样,behavior policy为β(a∣s)\beta(a|s)β(a∣s),target policy为π(a∣s,θ0)\pi(a|s,\theta_0)π(a∣s,θ0)

- DPG
前面的方法都是π(a∣s,θ)∈[0,1]\pi(a|s,\theta)∈[0,1]π(a∣s,θ)∈[0,1],神经网络拟合时输入s,输出不同a的π,这要求a的个数有限。
a=μ(s,θ)=.μ(s)a=\mu(s,\theta)\overset{.}=\mu(s) a=μ(s,θ)=.μ(s)J(θ)=E[vμ(s)]=∑s∈Sd0(s)vμ(s)J(\theta)=\mathbb{E}[v_\mu(s)]=\sum_{s∈\mathcal S}d_0(s)v_\mu(s) J(θ)=E[vμ(s)]=s∈S∑d0(s)vμ(s)