当前位置： 首页 > news >正文

2025年优化算法：雪雁优化算法（Snow Geese Algorithm，SGA）

news 2025/8/26 8:40:42

雪雁优化算法（Snow Geese Algorithm，SGA）的相关论文发表在科院二区期刊“APPLIED MATHEMATICAL MODELLING”上面。

01引言

雪雁算法（Snow Geese Algorithm，SGA）的灵感来自雪雁的迁徙行为，并模仿了雪雁迁徙过程中观察到的独特的“人字形”和“直线”形状的飞行模式。该算法分为三个主要阶段进行基准测试。在第一阶段，将雪雁算法的数值结果与使用相同测试函数和这些算法的原始数据的几种经典元启发式算法的结果进行比较。在第二阶段，为了最大限度地减少比较过程中的潜在变化，所有算法都在标准化测试平台上进行评估。第三阶段，本文应用雪雁算法解决了4个广为人知的工程优化问题：管柱设计、活塞杆优化设计、钢筋混凝土梁设计和汽车侧面碰撞设计。这些实际工程问题可作为评估雪雁算法解决问题能力的测试用例。雪雁算法的主要目标是为解决复杂的优化问题提供另一种视角。

02算法原理简介及算法实现流程（文末附代码）

一、算法来源

雪雁以其卓越的长距离迁徙而闻名，它们表现出卓越的合作飞行行为，可优化整个旅程的能源效率和耐力。这些行为包括形成独特的人字形和直线图案，这些图案可以动态适应不同的飞行条件。领头雁通过为整个鹅群创造有利的空气动力学条件，从而减少空气阻力并增强耐力，发挥着至关重要的作用。此外，较年轻或较弱的鹅在鸡群核心中的位置可以提供保护并减少风阻，使它们能够节省能量。

      1. 雪雁迁徙的集体行为

SGA 的灵感源自雪雁在秋季和冬季迁徙过程中的两种关键飞行模式：

人字形飞行模式（Herringbone Shape）：在迁徙初期，雪雁群体形成“人”字形队列，由领头雁带领飞行。这种模式优化了空气动力学，减少了整体空气阻力，帮助群体节省能量。领头雁创造有利的气流条件，使后续雁群（尤其是年轻或体弱的个体）位于队列核心区域，获得保护和能量保存优势。

直线形飞行模式（Straight Line Shape）：当迁徙接近目的地时，雪雁转为直线队列。这一阶段更注重效率，领头雁会轮换以避免疲劳，群体通过随机行为（如布朗运动）探索新路径，防止陷入局部最优路径。

这些行为体现了自然界中的自组织协作机制：群体动态调整飞行模式以应对环境变化（如风阻、能量消耗），确保整个群体在长途迁徙中的生存和成功。这种行为模式被抽象为算法的探索（Exploration）和利用（Exploitation）阶段，直接对应优化问题中的全局搜索和局部收敛过程。

关键洞察：雪雁的迁徙行为是一种高效的资源优化策略，SGA 通过数学建模将这些生物学观察转化为计算优化框架。

2. 行为建模：从生物学到数学

SGA 将雪雁个体的位置和速度映射为优化问题的潜在解，建立了严格的数学模型：

群体表示：每个雪雁个体被视为一个解（Solution），用位置矩阵 P 和速度矩阵 V 表示：

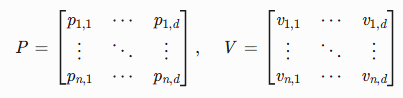
其中 n 为群体规模，d 为问题维度。

探索阶段（人字形模式）：

基于牛顿力学建模：引入空气阻力公式 和加速度更新（Eq. 8），模拟能量消耗与飞行动力学。

位置更新分三类（：

  • 适应度高的个体（前1/5）向全局最优位置靠近。

  • 弱势个体（后1/5）考虑中心位置以避免落伍。

  • 其余个体综合全局最优和随机扰动。该阶段鼓励群体在搜索空间中广泛探索。

利用阶段（直线形模式）

建模核心：算法通过变分问题和自适应参数将生物学行为转化为可计算的优化机制，确保在非平稳问题中平衡探索与利用。

3. 算法设计动机与创新

SGA 的提出是为了解决传统优化方法的局限性：

背景驱动：传统方法（如梯度下降）在高度非线性、多模态或约束工程问题中易陷入局部最优，且机器学习方法依赖大量数据易过拟合。SGA 受“No Free Lunch”定理启发，强调无单一算法适用于所有问题，需开发新型自然启发方法。创新点：双重停止准则：基于峭度检测和能量守恒，自适应控制模态分解数，避免过分解或欠分解。两阶段协同：人字形（探索）与直线形（利用）的切换机制（通过超参数 θ 实现），提升全局搜索能力。随机行为整合：布朗运动增强逃脱局部最优的鲁棒性，源于物理学中的随机过程理论。

算法框架 SGA=(R,U,T) 将初始化（R）、位置更新（U）和终止判断（T）模块化，确保流程可扩展。

总结：SGA 是首个将雪雁迁徙行为系统化为数学优化模型的算法，其来源融合了生物学观察、物理力学和随机过程理论，为复杂工程优化问题提供了新视角。

SGA 的核心来源是雪雁迁徙的协作飞行行为，通过严格的数学建模（位置更新、阻力计算、随机运动）转化为高效优化机制。其创新在于行为启发的两阶段协同和自适应控制，已在工程优化问题（如结构设计）中验证了有效性。这一自然启发的设计体现了多学科交叉的创新思维。

二、算法流程（结合代码）

1.初始化阶段

% 参数初始化
Pos = initialization(Np,D,Xmax,Xmin);  % 随机生成初始种群位置（Np个个体，D维问题）
Vel = zeros(Np,D);                    % 初始化速度矩阵为零
gBestScore = inf;                     % 全局最优分数设为无穷大
cg = zeros(1,Max_iter);                % 收敛曲线记录
% 计算初始适应度
for i = 1:Npfitness(i) = fobj(Pos(i,:));       % 评估每个个体的适应度
end
% 确定初始全局最优
[gBestScore, index] = min(fitness);    % 找出最优适应度及其索引
gBest = Pos(index,:);                  % 记录全局最优解
cg(1) = gBestScore;                    % 记录首轮收敛值

2.  主循环（迭代直到最大次数）

步骤1：飞行参数更新

coe = (4*(t/Max_iter))/exp(4*(t/Max_iter));  % 动态权重系数
fi = rand()*2*pi;                           % 随机生成飞行角度（0~2π）

步骤2：速度更新（牛顿力学模型）

for i = 1:Np    % 计算加速度（含空气阻力）    
acc = ((gBest - Pos(i,:)) - 1.29*Vel(i,:).^2*sin(fi))*10^-2;    % 更新速度    
Vel(i,:) = coe*Vel(i,:) + acc;
end

步骤3：种群排序与中心计算

[~,index] = sort(fitness);          % 按适应度升序排序
New_Pos = Pos(index,:);             % 重组位置矩阵
New_Vel = Vel(index,:);             % 重组速度矩阵% 计算种群加权中心
Xcaa = Pos .* fitness';                % 位置与适应度加权
Xc = sum(aa) / sum(fitness*Np);     % 加权平均中心

步骤4：位置更新（分模式处理）

Pos = Pos + Vel;  % 基础位移
if fi < pi  % 探索阶段（人字形模式）
for i = 1:Npif i <= Np/5  % 前1/5强者            
Pos(i,:) += a*(gBest - Pos(i,:)) + Vel(i,:);elseif i > Np/5 && i < 4*Np/5  % 中间3/5            
Pos(i,:) += a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) - c*(Pos(Np,:) + Pos(i,:)) + el(i,:);
else  % 后1/5弱者            
Pos(i,:) += a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) + Vel(i,:);
end        % 边界约束处理        
Pos(i,:) = min(max(Pos(i,:), Xmin), Xmax);endelse  % 利用阶段（直线模式）
if rand > 0.5  % 集体引导（50%概率）
for i = 1:Np            
Pos(i,:) += (Pos(i,:) - gBest)*rand;            
Pos(i,:) = min(max(Pos(i,:), Xmin), Xmax);endelse  % 布朗运动（50%概率）
for i = 1:Np            % 调用布朗运动函数生成随机步长            
Pos(i,:) = gBest + (Pos(i,:) - gBest).*rand.*Brownian(D);            
Pos(i,:) = min(max(Pos(i,:), Xmin), Xmax);
end
end
end

步骤5：适应度更新与全局最优维护

% 重新评估适应度
fori=1:Npfitness(i) = fobj(Pos(i,:));
end% 更新全局最优
fori=1:N
piffitness(i) < gBestScoregBestScore= fitness(i);        
gBest = Pos(i,:);    
end
end
% 记录收敛曲线
cg(t) = gBestScore;t = t + 1;  % 迭代计数增加

3. 布朗运动生成器

​​​​​​​functiono = Brownian(D)    
T = 1;                   % 时间步长   r = T/D;                 % 维度缩放因子    
dw = sqrt(r)*randn(1,D); % 生成D维高斯随机数    
o = cumsum(dw);          % 累积和生成布朗路径end

代码核心亮点：通过fi角度的随机生成实现自然的两阶段切换，布朗运动函数(Brownian)为逃离局部最优提供随机扰动，种群分组更新策略精准对应雪雁迁徙的生物学特性

03本文代码效果图

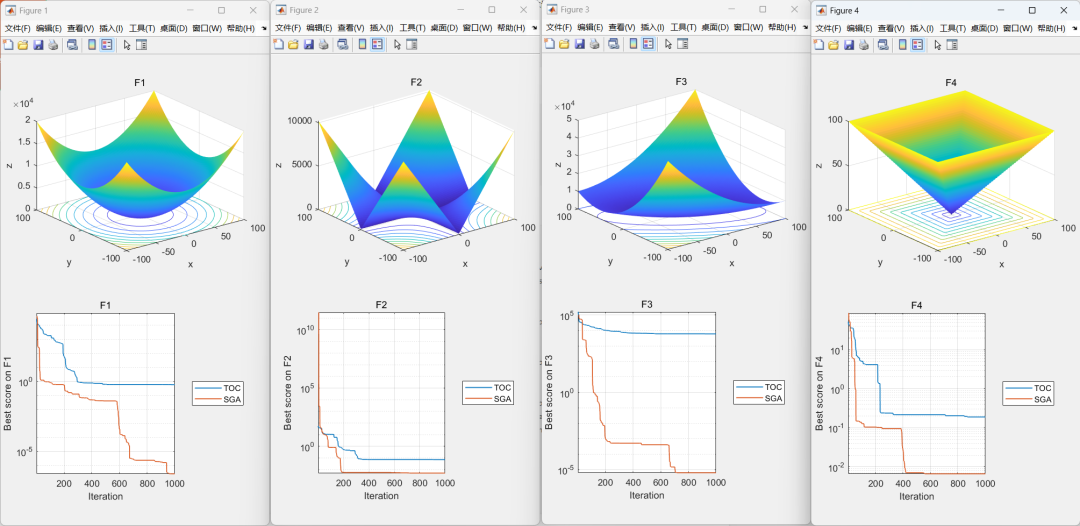
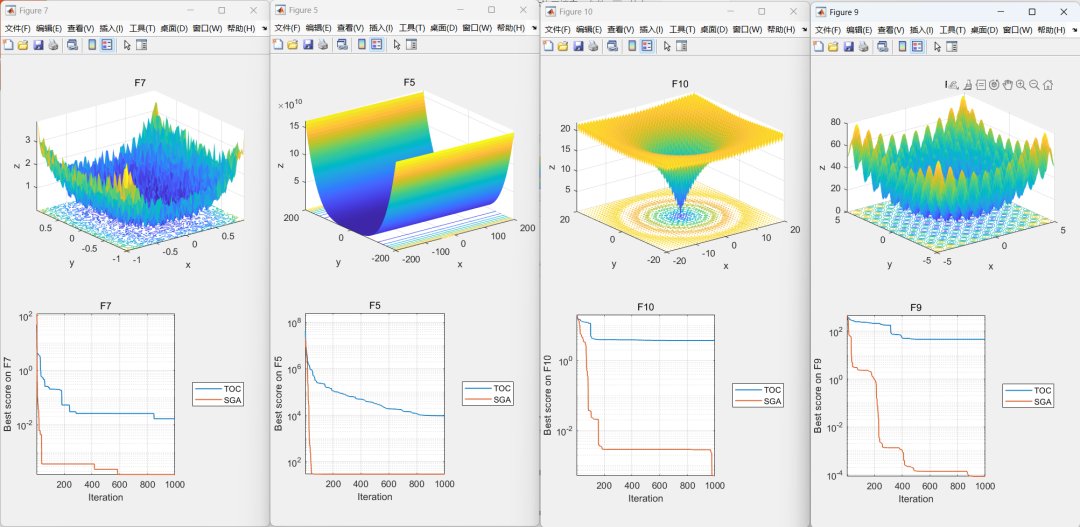
04部分代码

function [gBestScore,gBest,cg] = SGA6(Np, Max_iter, Xmin, Xmax, D, fobj)Pos = initialization(Np,D,Xmax,Xmin);
Vel = zeros(Np,D);gBest = zeros(1,D);
gBestScore = inf;
cg = zeros(1,Max_iter);for i = 1:Npfitness(i) = fobj(Pos(i,:));
end[gBestScore, index] = min(fitness);
gBest = Pos(index,:);cg(1) = gBestScore;t = 2;while t < Max_itercoe = (4*(t/Max_iter))/exp(4*(t/Max_iter));fi = rand()*2*pi;for i = 1:Npacc = ((gBest - Pos(i,:)) - 1.29*Vel(i,:).^2*sin(fi))*10^-2;Vel(i,:) = coe*Vel(i,:) + acc;end[~,index] = sort(fitness);for i = 1: NpNew_Pos(i,:) = Pos(index(i),:);New_Vel(i,:) = Vel(index(i),:);endPos = New_Pos;Vel = New_Vel;a = 4*rand() - 2;b = 3*rand() -1.5;c = 2*rand() - 1;for i =1:Npaa(i,:) = Pos(i,:)*fitness(i);bb(i) = Np*fitness(i);endXc = sum(aa)/sum(bb);Pos = Pos + Vel;if fi < pifor i = 1:Npif i<=1/5*NpPos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + Vel(i,:);    elseif  1/5*Np< i && i < 4/5*NpPos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) - c*(Pos(Np,:) + Pos(i,:))  + Vel(i,:);  elsePos(i,:) = Pos(i,:)  + a*(gBest - Pos(i,:)) + b*(Xc -Pos(i,:)) + Vel(i,:);  endFlag4ub=Pos(i,:)>Xmax;Flag4lb=Pos(i,:)<Xmin;Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;endelseif rand>0.5for i = 1:NpPos(i,:) = Pos(i,:) + (Pos(i,:) - gBest)*rand;Flag4ub=Pos(i,:)>Xmax;Flag4lb=Pos(i,:)<Xmin;Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;endelsefor i = 1:NpPos(i,:) = gBest + (Pos(i,:) - gBest).*rand.*Brownian(D);Flag4ub=Pos(i,:)>Xmax;Flag4lb=Pos(i,:)<Xmin;Pos(i,:)=(Pos(i,:).*(~(Flag4ub+Flag4lb)))+Xmax.*Flag4ub+Xmin.*Flag4lb;endendend        for i = 1:Npfitness(i) = fobj(Pos(i,:));endfor i=1:Npif gBestScore > fitness(i)gBest = Pos(i,:);gBestScore = fitness(i);endendt = t +1;cg (t) = gBestScore;
end
endfunction o = Brownian(D)T = 1;r = T/D;dw = sqrt(r)*randn(1,D);o = cumsum(dw);
end

✅作者简介:信号处理方向在校博士研究生,目前专研于MATLAB算法及科学绘图等，熟知各种信号分解算法、神经网络时序、回归和分类预测算法、数据拟合算法以及滤波算法。提供一个可以相互学习相互进步的平台

🚩技术信仰：知行合一，让每一行代码都成为解决问题的利器

🔍后台私信备注个人需求（比如TOC-BP）定制以下TOC算法优化模型（看到秒回）：

1.回归/时序/分类预测类：BP、RF、XGBoost、RBF、LSSVM、SVM、ELM、DELM、ESN、RELM等等均可，优化算法优化BP为例，可达到以下效果：

（1）优化BP神经网络的数据时序预测

（2）优化BP神经网络的数据回归(多输入多输出)预测

（3）优化BP神经网络的数据回归预测

2.分解类：EEMD、VMD、REMD、CEEMDAN、ICEEMDAN、SVMD等分解模型均可，优化算法优化VMD/ICEEMDAN为例，可达到以下效果：

（1）基于改进天鹰优化算法(IAO)优化的VMD参数

（2）基于改进天鹰优化算法(IAO)优化ICEEMDAN参数

3.去噪算法算法类：VMD/CEEMDAN/ICEEMDAN/SVMD+小波阈值/SVD去噪，可在去噪算法前加智能优化算法优化参数以VMD-WT/SVD为例，可达到以下效果：

（1）基于VMD-SpEn(样本熵)联合小波阈值去噪

（2）基于SVMD-SVD的信号去噪算法

（3）基于ZOA优化VMD-IAWT岩石声发射信号降噪算法

http://www.dtcms.com/a/350131.html

相关文章：

  • 2025 JVM 并发革命：虚拟线程与结构化并发，引领性能飞跃（35）
  • 京东前端社招面经
  • Pandas 高效数据处理：apply、向量化与分组
  • Qt——多媒体（音频、视频播放）
  • 艾利特石油管道巡检机器人：工业安全的智能守护者
  • 系统数据库
  • WRC2025 | 澳鹏亮相2025世界机器人大会，以数据之力赋能具身智能新纪元
  • 2025年9月计算机二级C++语言程序设计——选择题打卡Day6
  • 神经网络模型搭建及手写数字识别案例
  • 关于“程序=数据结构+算法”的深层认识
  • Java图形图像处理【双缓冲技术与游戏】【九】
  • Java全栈开发面试实战：从基础到微服务的深度解析
  • IDEA2022开启新版UI
  • 系统架构设计师备考第4天——计算机软件概述操作系统
  • Aligning Effective Tokens with Video Anomaly in Large Language Models
  • 储能防逆流：智能守护电网稳定的核心技术
  • 大数据毕业设计选题推荐-基于大数据的餐饮服务许可证数据可视化分析系统-Spark-Hadoop-Bigdata
  • 阿里云OSS文件上传_对象存储服务全流程
  • Android横竖屏切换的“数据保卫战”：如何优雅地保存和恢复表单数据
  • 用 python 开发一个可调用工具的 AI Agent，实现电脑配置专业评价_python ai agent
  • 常见前端性能优化讲解
  • 在分布式计算区域中通过VPC搭建私有网络
  • Ansible 任务控制与事实管理指南：从事实收集到任务流程掌控
  • Hadoop（四）
  • 【GPT入门】第59课 大模型内存计算指南：7B/8B/70B 模型在 32/16/8/4bit 精度下的内存需求测算
  • 【GPT5的多个子模型和动态路由分别是什么？】
  • 深度学习分类网络初篇
  • AI与自动化工具对比与选择
  • Coze用户账号设置修改用户密码-前端源码
  • 用一根“数据中枢神经”串起业务从事件流到 Apache Kafka