数学建模-整数规划(IP)

目录

1-AI带你认识IP(Integer Programming)

📘 整数规划（Integer Programming, IP）介绍

一、什么是整数规划？

1. 定义：

2. 直观理解：

二、整数规划的基本思想

三、整数规划的常见类型

1. ​​纯整数规划（Pure Integer Programming）​​

2. ​​混合整数规划（Mixed Integer Programming, MIP）​​

3. ​​0-1 整数规划（Binary / 0-1 Integer Programming）​​

四、整数规划的标准形式（以混合整数线性规划为例）

🎯 ​​目标：​​

📌 ​​约束条件：​​

🔢 ​​变量类型：​​

五、整数规划在数学建模中的常见用途

✅ 1. ​​0-1 整数规划典型应用：​​

✅ 2. ​​混合整数规划典型应用：​​

六、整数规划问题的求解方法

1. ​​分支定界法（Branch and Bound, B&B）​​

2. ​​割平面法（Cutting Plane Method）​​

3. ​​启发式算法 / 元启发式算法（用于大规模复杂问题）​​

4. ​​求解软件工具：​​

七、整数规划的优点与局限性

✅ 优点：

❌ 局限性：

八、在数学建模中的使用表述（参考写法）

九、总结一句话：

📌 类比总结（类比熵权法）：

✅ 拓展学习建议：

2-理论知识

定义

应用

0-1整数规划

蒙特卡洛模拟

作业

3-基于matlab实现整数规划

---

1-AI带你认识IP(Integer Programming)

📘 整数规划（Integer Programming, IP）介绍

---

一、什么是整数规划？

1. 定义：

​​整数规划（Integer Programming，简称 IP）​​ 是一类特殊的数学规划问题，在这类问题中，​​部分或全部决策变量被限制为整数​​（即只能取整数值，如 0, 1, 2, ...），而不是任意实数。

它是 ​​线性规划（Linear Programming, LP）的推广​​，但比线性规划 ​​更复杂、计算难度更大​​，因为整数约束使得可行解空间不再连续，无法直接使用单纯形法等传统线性规划算法高效求解。

---

2. 直观理解：

想象你要安排：

• •

  几台机器（只能买整数台，不能买半台）

• •

  派几个员工（不能派 2.5 个人）

• •

  选哪个项目做不做（是 or 否，0 或 1）

• •

  走哪条路径（节点访问顺序，整数表示）

这些问题中，​​变量必须为整数才有实际意义​​，这时候就需要用到 ​​整数规划​​。

---

二、整数规划的基本思想

在满足一系列线性（或非线性）约束条件下，​​寻找一组整数变量，使某个目标函数达到最大值或最小值​​。

与线性规划唯一不同的是：​​整数规划要求部分或全部变量必须是整数​​，这就引入了离散性与组合爆炸的可能性，使得问题通常更难求解，但也更贴合现实。

---

三、整数规划的常见类型

根据变量类型和约束条件的不同，整数规划可以分为以下几类 👇：

---

1. ​​纯整数规划（Pure Integer Programming）​​

• •

  ​​所有决策变量都必须取整数值​​

• •

  比如：x1​,x2​,...,xn​∈Z（即都是整数）

---

2. ​​混合整数规划（Mixed Integer Programming, MIP）​​

• •

  ​​部分变量为整数，部分变量可以为实数​​

• •

  比如：x1​,x2​∈Z，但 x3​,x4​∈R（可以是小数）

• •

  ​​这是数学建模中最常见的类型之一！​​

---

3. ​​0-1 整数规划（Binary / 0-1 Integer Programming）​​

• •

  ​​所有变量只能取 0 或 1​​

• •

  用于表示“是/否”、“选/不选”、“做/不做”等 ​​二元决策问题​​

• •

  比如：是否投资某项目？是否选择某路径？是否安排某人？

👉 ​​0-1 整数规划是整数规划中非常重要的特例，广泛用于组合优化、排班、选址、背包等问题。​​

---

四、整数规划的标准形式（以混合整数线性规划为例）

一个典型的 ​​混合整数线性规划（MILP）问题​​ 可以写成如下形式：

🎯 ​​目标：​​

Minimize (或 Maximize)Z=c1​x1​+c2​x2​+⋯+cn​xn​

📌 ​​约束条件：​​

⎩⎨⎧​a11​x1​+a12​x2​+⋯+a1n​xn​≤(或=,≥)b1​a21​x1​+a22​x2​+⋯+a2n​xn​≤(或=,≥)b2​⋯am1​x1​+am2​x2​+⋯+amn​xn​≤(或=,≥)bm​​

🔢 ​​变量类型：​​

x1​,x2​,…,xk​∈Z（整数变量）xk+1​,…,xn​∈R（连续变量，可取小数）

如果所有变量都是整数，则为纯整数规划；如果都只能取 0 或 1，则为 0-1 规划。

---

五、整数规划在数学建模中的常见用途

整数规划在实际建模问题中非常常见，尤其在需要 ​​做决策、选方案、排顺序、限个数​​ 的场景下，几乎必定涉及整数变量。例如：

---

✅ 1. ​​0-1 整数规划典型应用：​​

• •

  ​​方案选择问题​​：选哪些项目？选哪些路线？选哪些投资？

• •

  ​​任务分配问题​​：某任务分配给谁？（是/否）

• •

  ​​背包问题​​：选哪些物品放入背包，使得总价值最大但重量不超过限制

• •

  ​​选址问题​​：在哪些地方建厂/设点？（0 或 1 表示建或不建）

• •

  ​​排班问题​​：某员工在某天是否上班？

• •

  ​​TSP 旅行商问题（结合其他算法）​​

👉 这些问题往往可以建模为 ​​0-1 整数规划问题​​

---

✅ 2. ​​混合整数规划典型应用：​​

• •

  ​​生产计划问题​​：生产多少产品（整数或实数）、使用多少设备（整数）

• •

  ​​供应链与物流​​：建几个仓库（整数）、运输量（实数）

• •

  ​​网络设计问题​​：建多少基站（整数）、流量分配（实数）

• •

  ​​资源分配与优化​​：人员安排、资金分配、设备配置等

---

六、整数规划问题的求解方法

由于整数约束的存在，整数规划问题 ​​无法直接使用线性规划的单纯形法求解​​，常用的求解方法包括：

---

1. ​​分支定界法（Branch and Bound, B&B）​​

• •

  将问题分解为多个子问题（分支），并通过上下界剪枝（定界）逐步搜索最优解

• •

  是求解整数规划最常用的精确算法之一

---

2. ​​割平面法（Cutting Plane Method）​​

• •

  通过添加额外约束（割平面）逐步缩小可行域，逼迫解收敛到整数点

---

3. ​​启发式算法 / 元启发式算法（用于大规模复杂问题）​​

当问题规模很大、求解困难时，可使用：

• •

  遗传算法（GA）

• •

  模拟退火（SA）

• •

  粒子群优化（PSO）

• •

  蚁群算法（ACO）

• •

  等等...

这些方法 ​​不一定能得到全局最优解，但能在合理时间内获得较好的近似解​​，常用于竞赛或实际工程中。

---

4. ​​求解软件工具：​​

• •

  ​​Python：​​ PuLP、Pyomo、CVXPY、Gurobi、CPLEX 接口

• •

  ​​MATLAB：​​ intlinprog 函数（官方支持混合整数线性规划）

• •

  ​​Lingo / LINGO：​​ 专门用于线性和整数规划建模与求解

• •

  ​​Gurobi / CPLEX：​​ 商业优化求解器，性能极强（常用于数学建模竞赛进阶求解）

---

七、整数规划的优点与局限性

✅ 优点：

1. 1.

   ​​更贴近现实问题​​：很多实际问题中变量本来就是整数（人数、设备台数、是否选择等）

2. 2.

   ​​表达能力强​​：可以精确描述多种决策优化问题

3. 3.

   ​​求解精确​​：在合理时间内（尤其小规模、混合整数规划）能求得最优解

4. 4.

   ​​建模灵活​​：可与线性规划、非线性规划、动态规划等结合

❌ 局限性：

1. 1.

   ​​计算复杂度高​​：整数约束导致问题是 ​​NP 难问题​​，求解时间随问题规模指数增长

2. 2.

   ​​大规模问题难求解​​：变量和约束较多时，求解可能非常慢甚至不可行

3. 3.

   ​​对建模要求高​​：变量定义、约束设置不当会导致模型无解或偏离实际

4. 4.

   ​​需要专业工具​​：求解一般需要借助优化软件或编程实现

---

八、在数学建模中的使用表述（参考写法）

“本文针对 XX 问题，通过分析决策变量之间的逻辑关系与约束条件，构建了​​混合整数线性规划模型（MILP）​​，其中部分关键决策变量（如是否选择、是否建设、人员安排等）设定为整数变量（或 0-1 变量），以反映实际问题的离散特性。模型以 XX 为目标函数，以 XX 为约束条件，在此基础上利用 ​​Python 的 PuLP / Gurobi / MATLAB intlinprog​​ 等工具进行求解，得到最优决策方案。”

或者更简单的写法：

“考虑到某些决策变量（如选择、分配、建设等）必须为整数，本文构建了​​0-1 整数规划 / 混合整数规划模型​​，通过优化算法求解，确定了最优策略。”

---

九、总结一句话：

​​整数规划是一类要求部分或全部决策变量取整数值的数学优化方法，是线性规划的推广，能够更准确地描述现实中的离散决策问题，广泛应用于方案选择、资源分配、排班选址、组合优化等实际问题中，但其求解复杂度较高，常需借助专业算法与软件工具。​​

---

📌 类比总结（类比熵权法）：

对比维度	​​熵权法​​	​​整数规划​​
​​类型​​	一种客观赋权方法	一种数学优化方法
​​核心思想​​	利用信息熵衡量指标离散程度，确定客观权重	在一定约束下，寻找使目标最优的整数（或混合）变量取值
​​变量类型​​	无变量，只有指标数据	决策变量（可为整数、0-1、实数）
​​目标​​	确定各指标的权重，用于后续综合评价	优化某个目标函数（最大/最小），满足约束
​​适用问题​​	多指标综合评价中确定权重	方案选择、资源分配、调度、选址、组合优化等
​​输出结果​​	各指标的权重值	最优的决策方案（变量取值）
​​工具/方法​​	基于信息熵公式计算	建模 + 单纯形法扩展 / 分支定界 / 软件求解

---

✅ 拓展学习建议：

如果你对整数规划感兴趣，可以进一步了解：

• •

  ​​0-1 背包问题​​

• •

  ​​旅行商问题（TSP）与车辆路径问题（VRP）​​

• •

  ​​指派问题（Assignment Problem）​​

• •

  ​​设施选址问题（Facility Location）​​

• •

  ​​混合整数非线性规划（MINLP）​​

• •

  ​​整数规划在数学建模竞赛中的真题案例（如国赛、美赛）​

2-理论知识

定义

应用

0-1整数规划

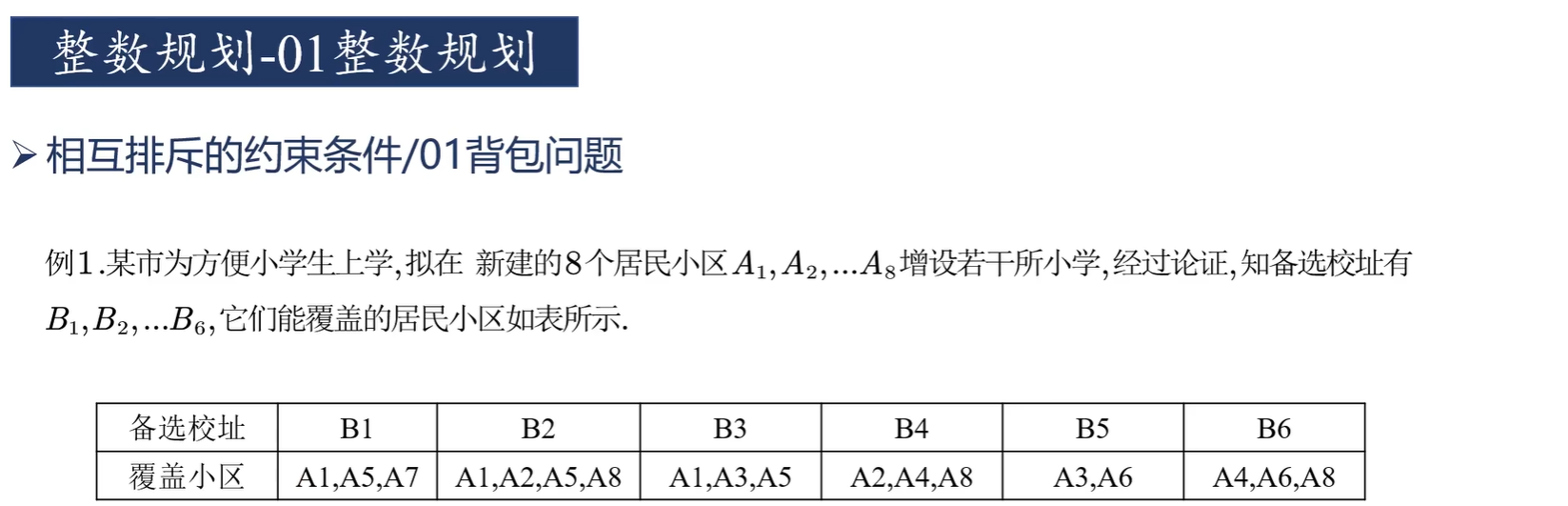
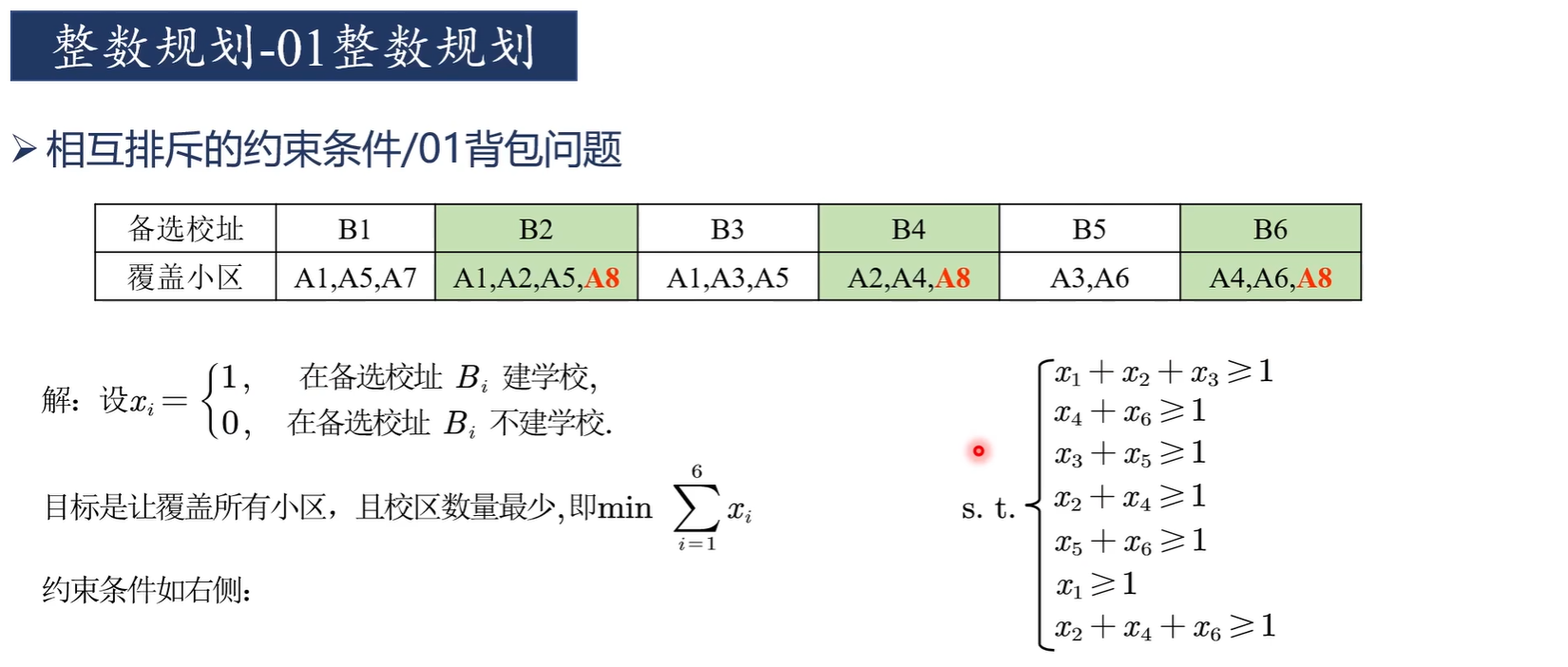
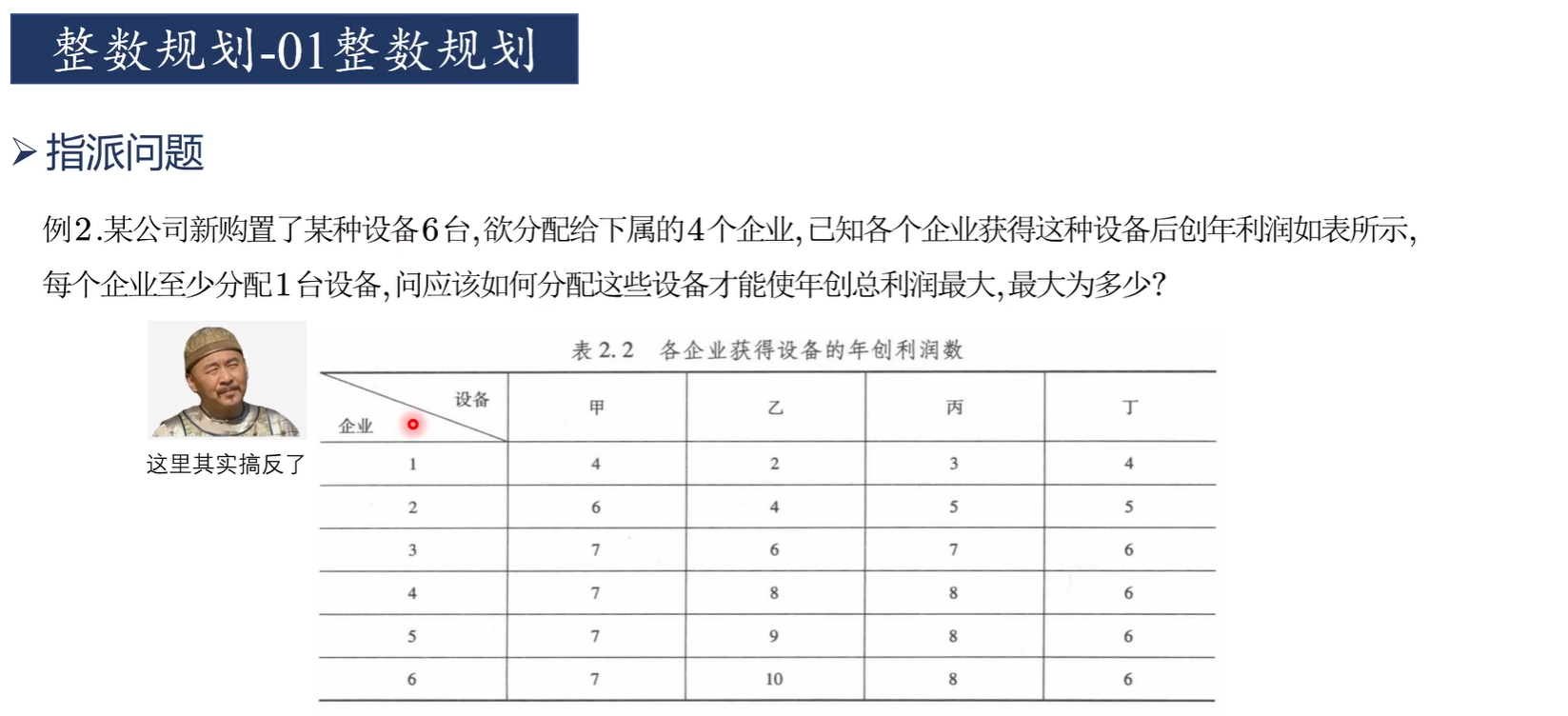
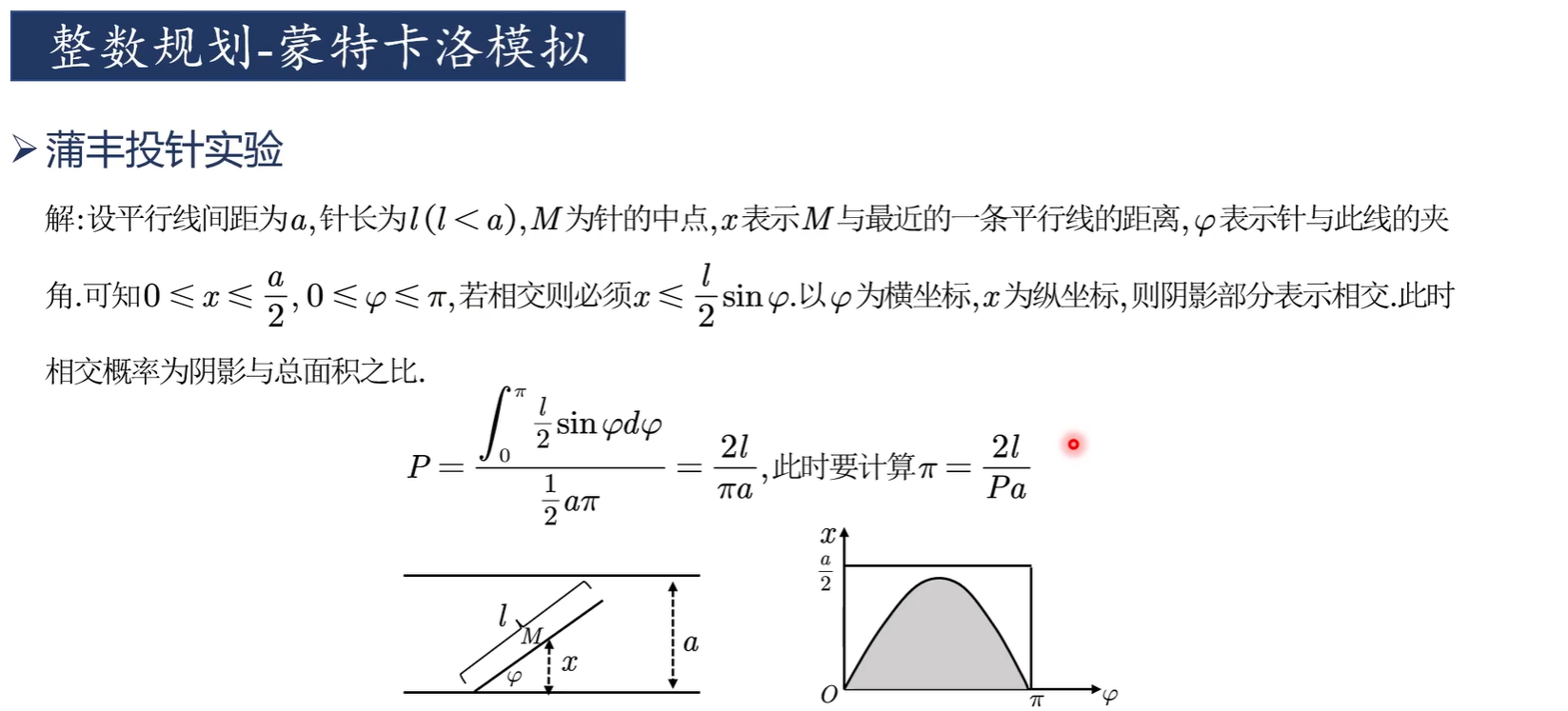
蒙特卡洛模拟

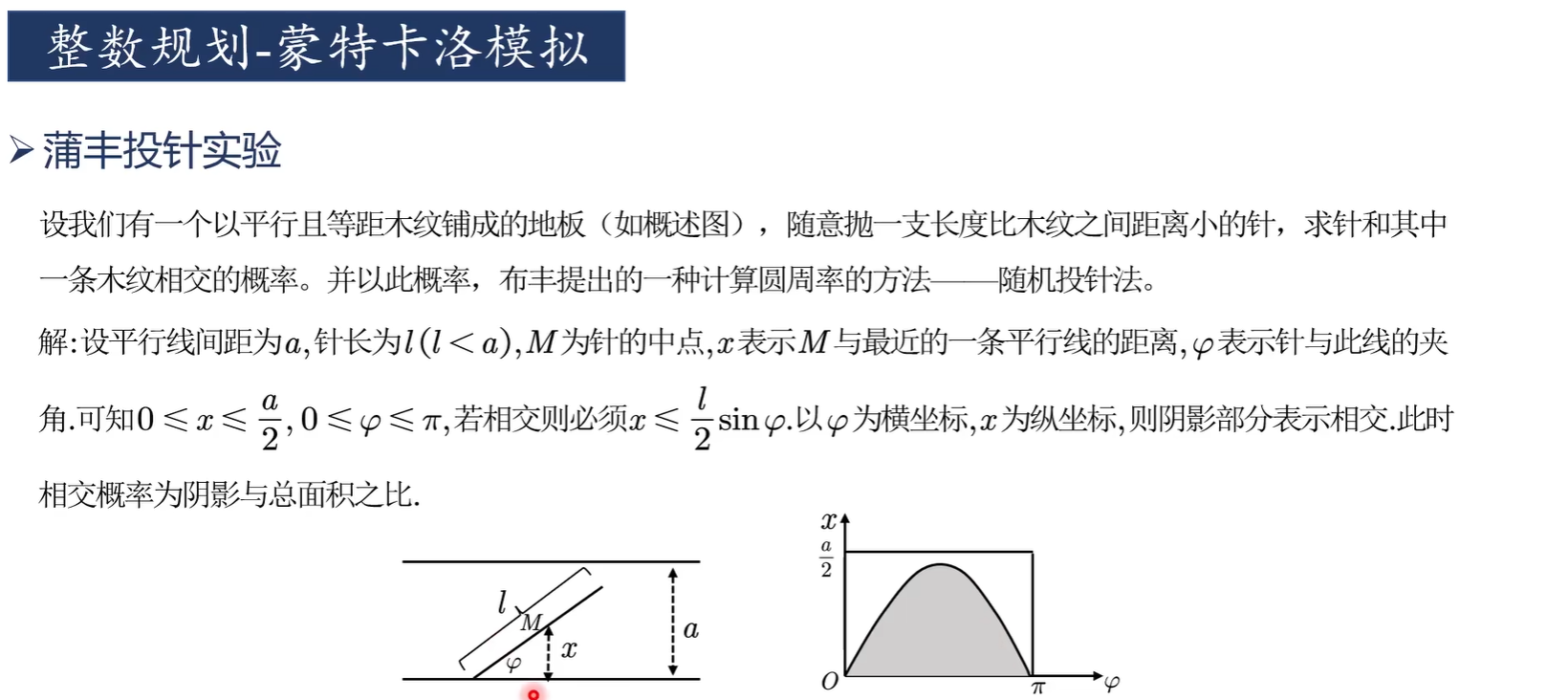
作业

3-基于matlab实现整数规划