大模型知识点之矩阵乘以向量

说明：本文开始总结大模型使用到的知识点。很零散，但重要。
矩阵乘以向量的几何意义
说明：
矩阵乘以向量的几何意义如下：⚠️警告：升维降维那我说的是 Ax 这个顺序相乘（矩阵在左边向量在右边）
1、矩阵乘以向量的的前提是列数必须等于向量的维度。否则无法对应每个输入维度进行加权求和。这是规则，但是为什么会有这个规则呢？具体参考 为什么矩阵乘以向量要求矩阵列数等于向量维度
2、当矩阵的行数不等于向量的维度的时候（列数必须等于向量的维度），相当于做了升维（矩阵行数大于向量维度）或者降维（矩阵行数小于向量维度），另外也做了拉伸（非单位矩阵）等操作。
3、当矩阵的行数等于向量的维度的时候（列数必须等于向量的维度），相当于只做了拉伸（非单位矩阵）等操作。

升维

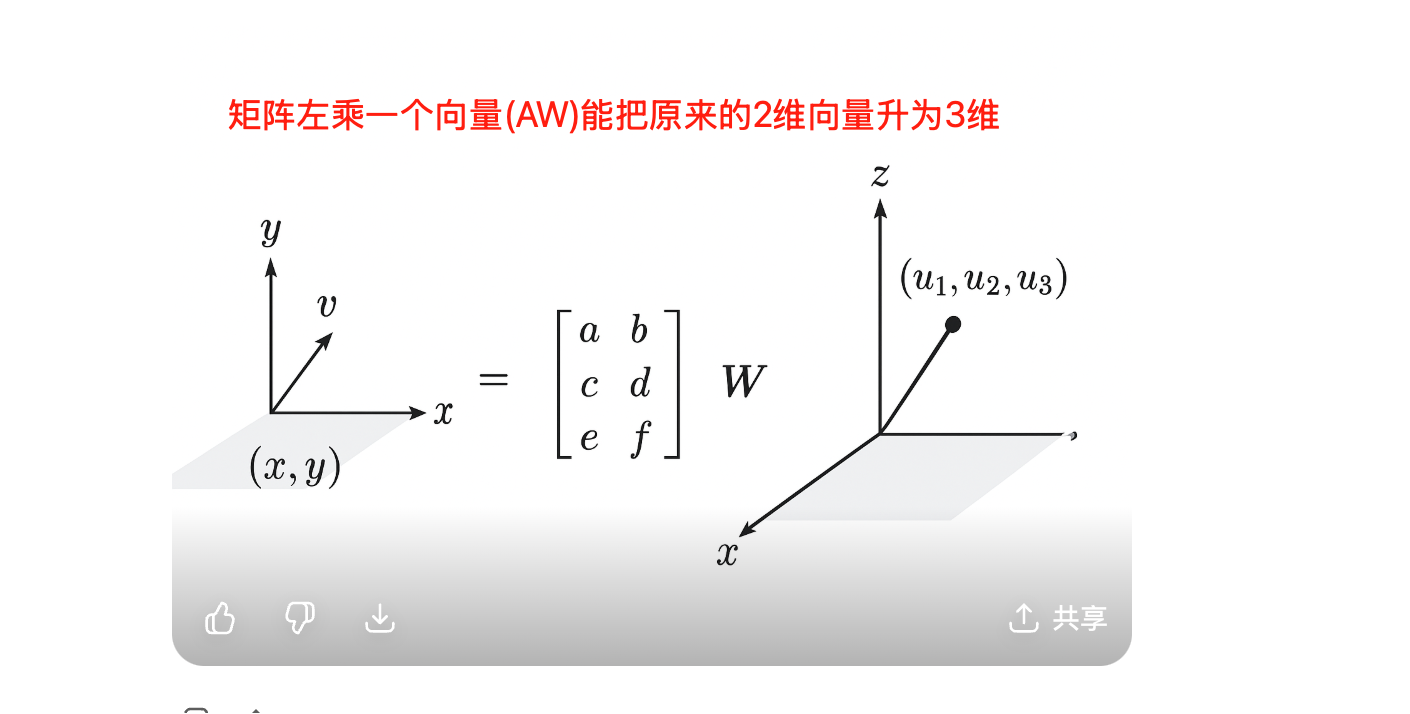
拉伸
注意

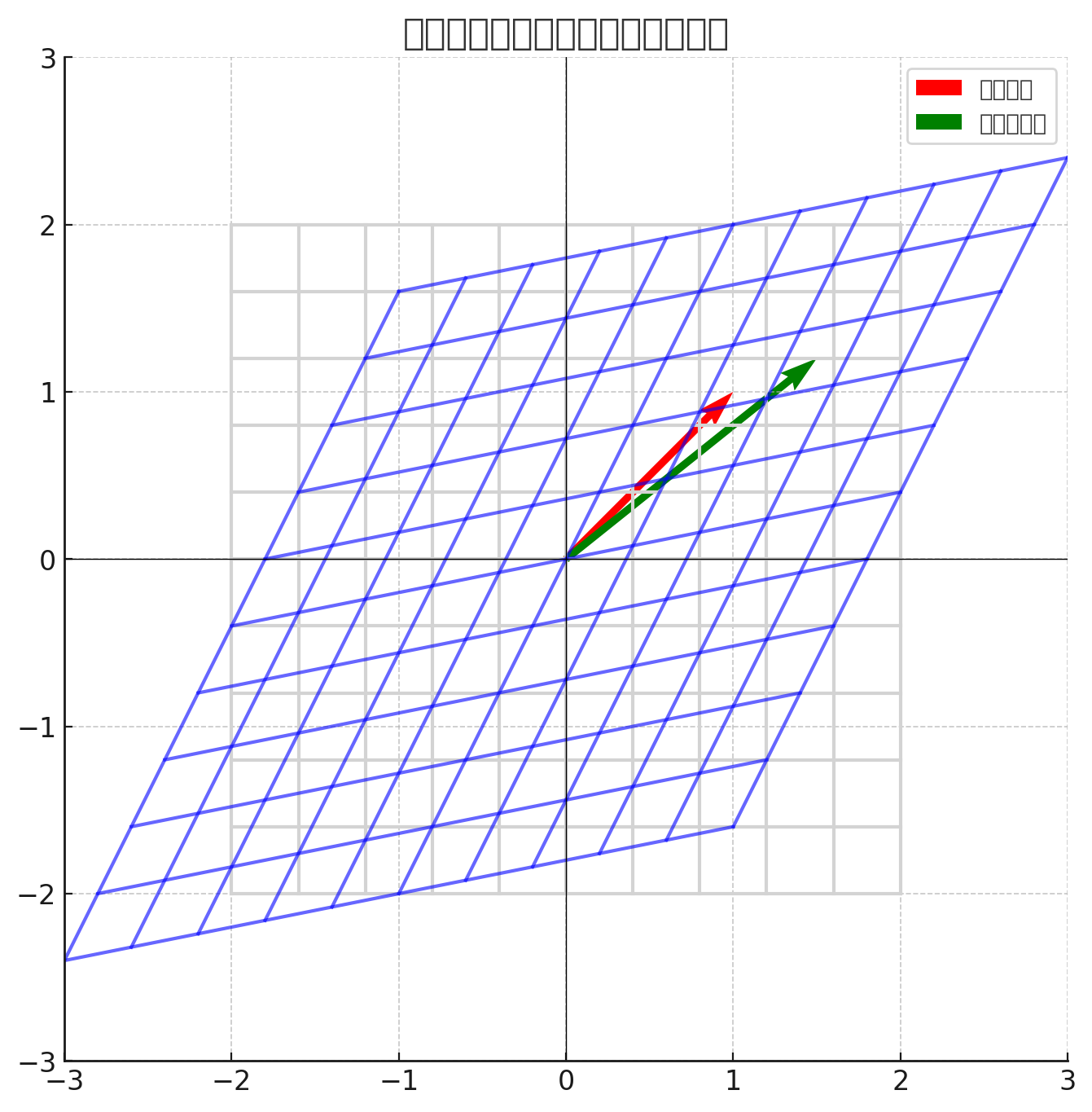
上图就是 矩阵乘向量的几何意义：

灰色网格：原始坐标系

蓝色网格：矩阵作用后的坐标系（整个平面被拉伸+错切）

红色箭头：原始向量

绿色箭头：矩阵变换后的向量

👉 所以：矩阵乘以向量 = 向量在空间中被线性变换。