当前位置：首页 > news >正文

【数学建模】如何总结数学建模中的层次分析法最好

news 2025/8/26 6:39:42

模型简介

模型名称：层次分析法
核心问题类型：评价类
核心思想和适用场景
- 核心思想：将大决策问题拆解成小比较问题，通过数学计算综合最终结论：本质是人的主观判断转换为客观数据的工具
- [[适用场景]]
  - 个人决策
  - 企业 / 项目决策
  - 综合评价
核心步骤与流程图：
- 核心步骤：
  1. [[构建层次结构]]
    1. 目标层
    2. 准则层
    3. 方案层
  2. 构造判断矩阵
    1. 两两比较法/优劣度
      1. 用 1-9 标度法赋值
    2. 生成两类矩阵
      1. 准则层重要性矩阵
      2. 方案层在各准则下的优劣矩阵
  3. 计算权重 + 单层次一致性检验
    - [[计算权重]]
  4. 层次总排序 + 总一致性检验
    - [[总权重计算]]
    - [[总一致性检验]]
  5. 选择总权重最高的方案作为最优解
- 流程图
数学公式/表达式
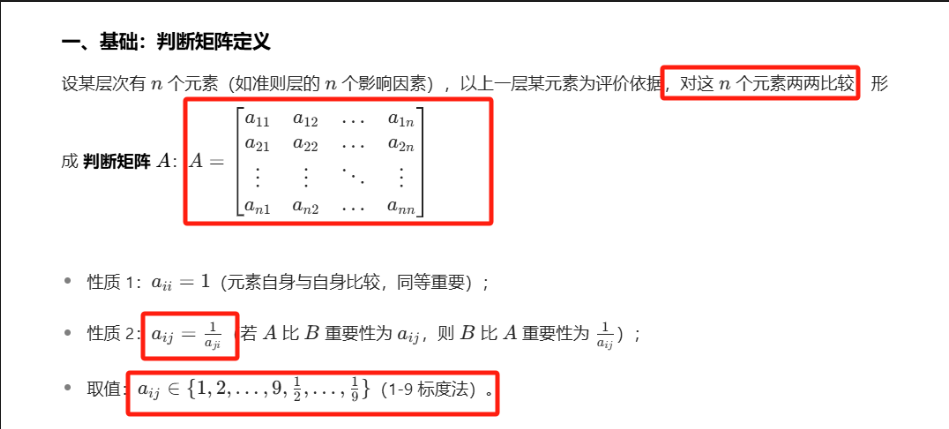
1. 基础：[[判断矩阵定义]]
2. 核心 1：权重计算
  1. [[特征值法]]（优先级高）
  2. [[和法]]
  3. [[根法]]
3. 核心 2：一致性检验（避免主观判断矛盾）
  - 步骤一：[[一致性指标CI]]
  - 步骤二：[[平均随机一致性指标RI]]
  - 步骤三：[[一致性比例CR]]
4. [[层次总排序]]（合成最终权重）
- [[套路]]

获取判断矩阵

代码：

disp('请输入判断矩阵A')%相当于printfA=input('A=');%相当于scanf，输入函数[n,m] = size(A);
size(A)函数是用来求矩阵A的大小的,它返回一个行向量，第一个元素是矩阵的行数，第二个元素是矩阵的列数

方法1： [[算术平均法求权重]]

Sum_A = sum(A); %将A矩阵按列求和
SUM_A = repmat(Sum_A,n,1);
%B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。
Stand_A = A ./ SUM_A;
disp('算术平均法求权重的结果为：');
w1 = sum(Stand_A,2)./n;
disp(w1)

[[SUM_A = repmat(Sum_A,n,1);（主要做算术平均法的分母）]]
将列和向量 Sum_A 复制成与原矩阵 A 同维度的矩阵
- [[Stand_A ]]= A ./ SUM_A
  对原矩阵 A 进行列归一化
[[w1]] = sum(Stand_A,2)./n; %n=3，2是行求和的意思
计算最终权重

方法二：特征值法求权重

[V,D] = eig(A);%求特征值Max_eig = max(max(D));% 先按列求最大值，得到行向量，再从这个向量里面求最大值[r,c]=find(D == Max_eig , 1);disp('特征值法求权重的结果为：');w2 = V(:,c) ./ sum(V(:,c));disp(w2)disp('两种方法的平均权值为：');disp((w1 + w2) ./ 2);

还是用3*3的A举例

[[[V,D] = eig(A);]]
特征值和特征向量
[[Max_eig = max(max(D));]]
提取最大特征值
[[ [r,c] = find(D == Max_eig , 1)]]
定位最大特征值在矩阵 D 中的列索引
[[w2]] = V(:,c) ./ sum(V(:,c));
计算特征值法的权重向量
(w1 + w2) ./ 2
将算术平均法得到的 w1 与特征值法得到的 w2 取平均值

计算一致性比例CR（优先计算）

CI = (Max_eig - n) / (n-1);RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %这里的RI最多支持 n = 15，注意检查！% 这里n=2时，RI=0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数CR=CI/RI(n);disp('最大特征值为:');disp(Max_eig);disp('一致性指标CI=');disp(CI);disp('一致性比例CR=');disp(CR);if CR<0.10disp('CR<0.10，该判断矩阵A的一致性可以接受!');elsedisp('注意：CR >= 0.10，该判断矩阵需要进行修改!');end

若 (CR < 0.1)：判断矩阵矛盾可接受，权重有效；
若 (CR \geq 0.1)：需调整判断矩阵（如修改两两比较的赋值），
直至 (CR < 0.1)。·

源代码：

%% 层次分析法% 只有非一致矩阵才需要一致性检验% % 要先进行一致性检验，通过后才能求权重，我们这里为了方便讲解才放到了最后做的一致性检验%% 获取判断矩阵disp('请输入判断矩阵A')A=input('A=');[n,n] = size(A);%% 方法1： 算术平均法求权重Sum_A = sum(A); %将A矩阵按列求和SUM_A = repmat(Sum_A,n,1);%B = repmat(A,m,n):将矩阵A复制m×n块，即把A作为B的元素，B由m×n个A平铺而成。Stand_A = A ./ SUM_A;disp('算术平均法求权重的结果为：');w1 = sum(Stand_A,2)./n;disp(w1)%% 方法2： 特征值法求权重[V,D] = eig(A);Max_eig = max(max(D));% 先按列求最大值，得到行向量，再从这个向量里面求最大值[r,c]=find(D == Max_eig , 1);disp('特征值法求权重的结果为：');w2 = V(:,c) ./ sum(V(:,c));disp(w2)disp('两种方法的平均权值为：');disp((w1 + w2) ./ 2);%% 计算一致性比例CRCI = (Max_eig - n) / (n-1);RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %这里的RI最多支持 n = 15，注意检查！% 这里n=2时，RI=0，我们为了避免分母为0，将这里的第二个元素改为了很接近0的正数CR=CI/RI(n);disp('最大特征值为:');disp(Max_eig);disp('一致性指标CI=');disp(CI);disp('一致性比例CR=');disp(CR);if CR<0.10disp('CR<0.10，该判断矩阵A的一致性可以接受!');elsedisp('注意：CR >= 0.10，该判断矩阵需要进行修改!');end

查看全文

http://www.dtcms.com/a/349592.html