深度学习入门第一课——神经网络实现手写数字识别

昨天我们讲了深度学习的大致框架，下面我们用深度学习网络来实现一个小项目——手写数字识别。

完整代码

import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensortraining_data=datasets.MNIST(root='./data',train=True,download=True,transform=ToTensor())test_data=datasets.MNIST(root='./data',train=False,download=True,transform=ToTensor())from matplotlib import pyplot as plt, figurefigure = plt.figure()
for i in range(9):image,label = training_data[i+59000]figure.add_subplot(3,3,i+1)plt.title(label)plt.axis('off')plt.imshow(image.squeeze(),cmap='gray')a=image.squeeze()
plt.show()train_dataloader=DataLoader(training_data,32)
test_dataloader=DataLoader(test_data,32)device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)for X, y in test_dataloader:print(f"Shape of X [N, C, H, W]: {X.shape}")  # 批次大小、通道、高度、宽度print(f"Shape of y: {y.shape}, Type of y: {y.dtype}")breakclass Net(nn.Module):def __init__(self):super().__init__()self.flatten = nn.Flatten()self.hidden1 = nn.Linear(28*28,128)self.hidden2 = nn.Linear(128,400)self.output = nn.Linear(400,10)def forward(self, x):x = self.flatten(x)x = self.hidden1(x)x = nn.ReLU()(x)# x = nn.functional.sigmoid(x)x = self.hidden2(x)x = nn.ReLU()(x)# x = nn.functional.sigmoid(x)x = self.output(x)return xmodel = Net()
model.to(device)
loss_fn = nn.CrossEntropyLoss()
# optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)def train(train_dataloader,model,loss_fn,optimizer):model.train()batch_size_num=1for X, y in train_dataloader:X,y=X.to(device),y.to(device)output = model.forward(X)loss = loss_fn(output,y)optimizer.zero_grad()loss.backward()optimizer.step()a=loss.item()if batch_size_num %100 ==0:print(f"Batch size: {batch_size_num}, Loss: {a}")batch_size_num+=1# print(model)def test(dataloader,model,loss_fn):size = len(dataloader.dataset)num_batches = len(dataloader)model.eval()batch_size_num=1loss,correct=0,0with torch.no_grad():for X, y in test_dataloader:X,y=X.to(device),y.to(device)pred = model(X)loss = loss_fn(pred,y)+losscorrect += (pred.argmax(1) == y).type(torch.float).sum().item()loss/=num_batchescorrect/=sizeprint(f'Test result: \n Accuracy: {(100*correct)}%,Avg loss: {loss}')# train(train_dataloader,model,loss_fn,optimizer)
# test(test_dataloader,model,loss_fn)epochs=10
for i in range(epochs):print(f"Epoch {i+1}")train(train_dataloader,model,loss_fn,optimizer)test(test_dataloader,model,loss_fn)

结果展示

下面我来进行拆解，

 1 导入库

import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor

前面就是导入库，没什么多说的。

2 导入数据

training_data=datasets.MNIST(root='./data',train=True,download=True,transform=ToTensor())test_data=datasets.MNIST(root='./data',train=False,download=True,transform=ToTensor())

首先我们从datasets.MINST()这个库中导入数据

从上面我们可以看出，这个库中包含一些网址，然后可以从其中下载一些数据。

root='./data',        这个表示把数据存储在这样一个文件夹中
train=False,        这个表示下载的是训练集还是测试集，True为训练集，False为测试集
download=True,        下载
transform=ToTensor())        转化为Tensor数据，将图像数据转换为PyTorch张量（像素值归一化到[0,1]）。

3 数据展示

from matplotlib import pyplot as plt, figurefigure = plt.figure()
for i in range(9):image,label = training_data[i+59000]figure.add_subplot(3,3,i+1)plt.title(label)plt.axis('off')plt.imshow(image.squeeze(),cmap='gray')a=image.squeeze()
plt.show()

• 创建一个3x3的子图，显示训练集中最后9个样本（索引59000到59008）的图像和标签。
• image.squeeze()将形状从[1,28,28]变为[28,28]，因为matplotlib要求单通道图像为二维。

结果展示

4 创建数据加载器

train_dataloader=DataLoader(training_data,32)
test_dataloader=DataLoader(test_data,32)

• 训练和测试数据加载器，每次迭代返回一个批次（32张图片和对应的标签）。

5 ​设置设备

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)

• 检查是否有可用的GPU，如果有则使用第一个GPU，否则用CPU。

6 打印一批测试数据的形状

for X, y in test_dataloader:print(f"Shape of X [N, C, H, W]: {X.shape}")  # 批次大小、通道、高度、宽度print(f"Shape of y: {y.shape}, Type of y: {y.dtype}")break

• 从测试数据加载器中取一个批次，打印输入图像和标签的形状。
• X的形状：[32, 1, 28, 28]（32个样本，1个通道，28x28像素）
• y的形状：[32]（32个标签）

7 ​定义神经网络模型

class Net(nn.Module):def __init__(self):super().__init__()self.flatten = nn.Flatten()self.hidden1 = nn.Linear(28 * 28, 128)  # 第一层全连接self.hidden2 = nn.Linear(128, 400)     # 第二层全连接self.output = nn.Linear(400, 10)       # 输出层（10个数字）def forward(self, x):x = self.flatten(x)        # 将图像展平为向量：[batch, 28 * 28]x = self.hidden1(x)        # [batch, 128]#x = nn.functional.sigmoid(x)x = nn.ReLU()(x)           # ReLU激活x = self.hidden2(x)        # [batch, 400]#x = nn.functional.sigmoid(x)x = nn.ReLU()(x)           # ReLU激活x = self.output(x)         # [batch, 10]return x

• 一个简单的多层感知机（MLP）模型：
  • 输入：28x28=784维
  • 两个隐藏层：128和400个神经元，使用ReLU激活。
  • 输出层：10个神经元（对应0-9），无激活（后面用交叉熵损失包含Softmax）。

forward为前向传播

        第一步先用flatten(x)把数据拉成一维的，例如原本28*28的二维数据，变成了28*28的一维数据

        第二步传入到隐含层

        第三步使用激活函数进行激活（这里初开始使用sigmod函数进行激活，但使用ReLU激活比较好）

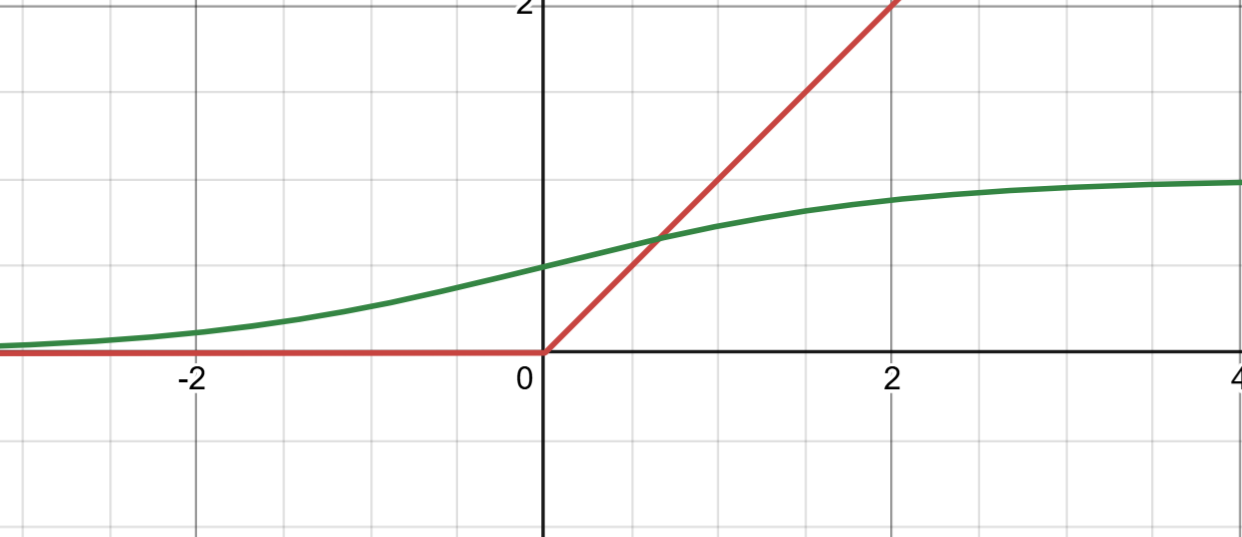
sigmod和ReLU函数对比

Sigmoid 激活函数的公式为： f(x) = 1 / (1 + e^(-x)) 它将输入值映射到 (0, 1) 区间，常用于二分类问题的输出层。Sigmoid 的优点是可以提供概率分布，但存在以下问题：

• 梯度消失问题：当输入值过大或过小时，梯度趋近于 0，导致深层网络训练困难。

• 非零中心输出：输出值始终为正，可能导致权重更新不稳定。

• 计算复杂度高：涉及指数运算，计算效率较低。

ReLU 激活函数的公式为： f(x) = max(0, x) ReLU 是深度学习中广泛使用的激活函数，具有以下优点：

• 计算效率高：只需简单的比较操作，计算速度快。

• 避免梯度消失：在正值范围内梯度为常数，有助于深层网络的训练。

• 稀疏激活性：部分神经元输出为 0，减少参数依赖，缓解过拟合问题。

然而，ReLU 也存在死亡 ReLU问题，即当神经元进入负值区域时，梯度为 0，可能导致神经元永不激活。为此，改进版本如 Leaky ReLU 和 Parametric ReLU 被提出。

对比总结：

• 计算效率：ReLU 优于 Sigmoid，适合处理大规模数据。

• 梯度问题：Sigmoid 易出现梯度消失，而 ReLU 在正值范围内表现更优。

• 适用场景：Sigmoid 常用于二分类问题的输出层，而 ReLU 更适合深度网络，如图像识别和自然语言处理任务

• 

8 创建模型对象

model = Net()
model.to(device)

这里创建了一个模型对象，并把模型传入到我们的device也就是GPU中

9 初始化损失函数

loss_fn = nn.CrossEntropyLoss()

然后定义损失函数，这里为交叉熵损失函数。因为分类算法一般都是用交叉熵损失函数，找最优参数。还有许多损失函数的介绍看我主页。

10 建立优化器

# optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

这里最初建立的是SGD优化器，这个是梯度下降优化器，lr步长为0.01，后面优化成了Adam优化器，这个比较实用。适用几乎所有哦网络。

11 创建训练函数

def train(train_dataloader,model,loss_fn,optimizer):model.train()batch_size_num=1for X, y in train_dataloader:X,y=X.to(device),y.to(device)output = model.forward(X)loss = loss_fn(output,y)optimizer.zero_grad()loss.backward()optimizer.step()a=loss.item()if batch_size_num %100 ==0:print(f"Batch size: {batch_size_num}, Loss: {a}")batch_size_num+=1# print(model)

第一步model.train()，这里设置为训练模式（影响 Dropout、BatchNorm 等层），也就是说允许读写w。

第二部 分批次对训练集进行导入，前行传播，计算损失值，清空之前的梯度，反向计算梯度，更新梯度，下面就是训练100批次就打印一下损失值。

12 创建测试函数

def test(dataloader, model, loss_fn):size = len(dataloader.dataset)     # 总样本数num_batches = len(dataloader)      # batch 数量model.eval()                       # 设置为评估模式batch_size_num = 1loss, correct = 0, 0with torch.no_grad():  # 不计算梯度，节省内存和计算for X, y in dataloader:X, y = X.to(device), y.to(device)pred = model(X)loss += loss_fn(pred, y)  # 累积损失correct += (pred.argmax(1) == y).type(torch.float).sum().item()  # 统计正确预测的数量loss /= num_batches                # 平均损失correct /= size                    # 正确率print(f'Test result: \n Accuracy: {(100*correct):.2f}%, Avg loss: {loss:.4f}')

我们先把总样本数求出来是因为后面要用预测对的样本数/总样本数就可以得到准确率了

model.eval()就是把w的模式改为仅读模式

初始化损失值和准确率

在不对梯度进行改变的情况下，对训练集中每一个值进行循环，得到预测值，然后用预测值和真实值作对比，然后得出的是一个列表，其中全是True和False.然后转化为float也就是转化为数值型0/1，然后再sum求综合再取item()。

然后计算平均损失和正确率（其实这里损失值没啥用了）

13 训练和测试

train(train_dataloader,model,loss_fn,optimizer)
test(test_dataloader,model,loss_fn)

这里进行了训练和测试，结果并不是很理想，但是我们可以叠加训练，也就是说，在优化的时候次数太少，w权重并没有更新到最优状态。然后我们叠加train,这也是深度学习的一个优点，可以在前一层的基础上继续训练。

epochs=10
for i in range(epochs):print(f"Epoch {i+1}")train(train_dataloader,model,loss_fn,optimizer)test(test_dataloader,model,loss_fn)

如上，我们进行了十次训练，准确率从0.87训练到了95