关于熵减 - 电子圆柱
下面我们继续讨论自提升系统的另一个实现方法:双线线圈。
首先根据已知单位计算磁场强度的单位,特斯拉![]() ,
,
![]()
![]()
![]()
![]()
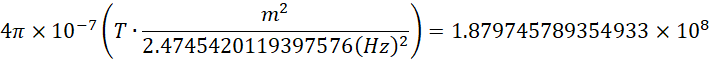
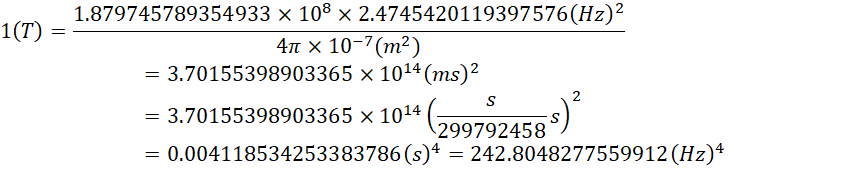
另一种结果,
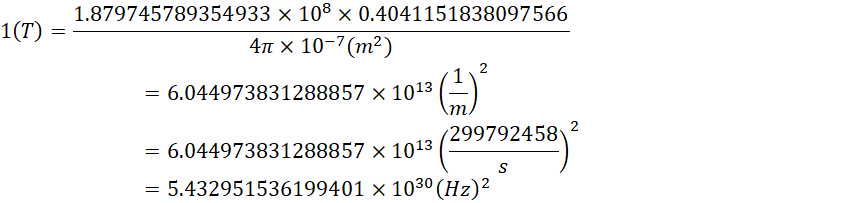
按照米秒制,它的单位是赫兹的四次方或者赫兹的平方。
![]()
相距为R的两根平行长直导线,各自在距离为R处产生的磁场强度为,
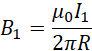
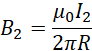
![]() 受到
受到![]() 产生的磁场安培力的大小,
产生的磁场安培力的大小,
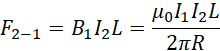
![]() 受到
受到![]() 产生的磁场安培力的大小,
产生的磁场安培力的大小,
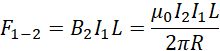
同向电流时大小相等方向相反,反向电流时大小相等方向相同。通常情况下这两者用的力是磁场力。对于非对称电容来说,两个极板共用同一个电场,而极板的面积大小不同,就造成了极板两端的光速差异。我们可以考虑类似的情况,两条平行导线,通过通入电流而构成同一个磁场(可能是相吸或者相斥),电流的大小可以相同,但是导线的长度不能相同。或者导线的长度相同,电流作用的时间不同。因为导线的长度不容易改变,所以我们考虑改变电流作用的时间。如果确定了单位时间,那么剩下的即使电流的频率。
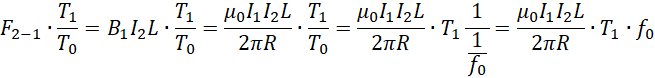
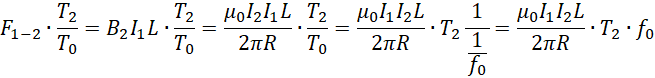
这里的![]() 是电子频率。从前面出现的,
是电子频率。从前面出现的,
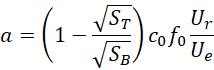
可以看出![]() 对应于
对应于![]() ,也就是说电子对的频率中心距离的比率对应于电压的比率,
,也就是说电子对的频率中心距离的比率对应于电压的比率,
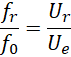
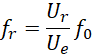
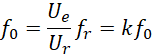
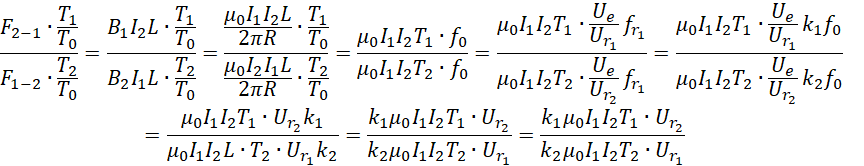
这里T和U相互独立,且,
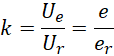
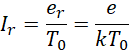
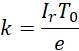
一旦![]() 确定
确定![]() 就确定了,如果两个力在时间上的作用效果相同(限制为不输出的内力即可),
就确定了,如果两个力在时间上的作用效果相同(限制为不输出的内力即可),
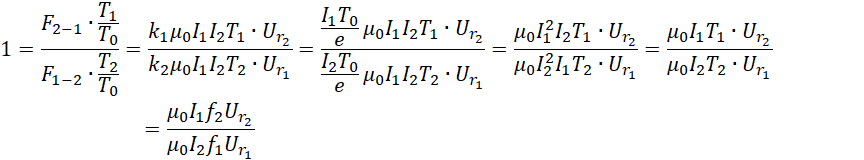
这里的![]() 为外部输入电流的频率,
为外部输入电流的频率,
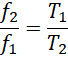
继续推导,
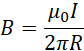
![]()
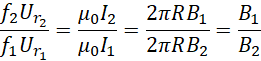
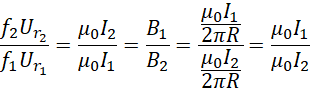
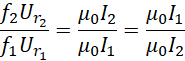
这就要求如果![]() 不变,
不变,![]() 和
和![]() 总是相等,且外部输入的频率和电压必须保证,
总是相等,且外部输入的频率和电压必须保证,
![]()
但这是无法保证的,因为外部输入的电压和频率不可能受控于内部的磁场。所以,![]() 必须可以发生变化。但由于真空磁导率确实为虚数单位和常数的乘积,所以,
必须可以发生变化。但由于真空磁导率确实为虚数单位和常数的乘积,所以,
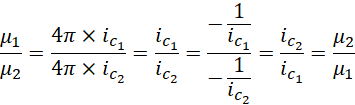
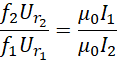
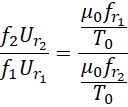
假定![]() 不随其它量改变,
不随其它量改变,
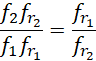
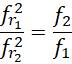
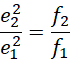
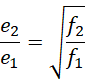
也就是说,最终输入的频率的比率会控制电子的频率的平方的比率。或者说输入的频率比的平方根,决定两条导线中电子电量的比率或者电子的频率的比率。观察光速的表达式,
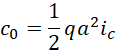
可见它并不涉及电子频率的数值。但是,如果认为
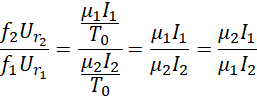
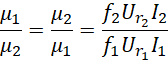
不难发现由于![]() 具有虚数单位性质,它和它自己的负倒数相等,所以两种不同的真空磁导率的比值和比值的倒数相等。这就说明两种真空磁导率是同时存在的。可以通过调节电流电压和频率来使得它发生变化。但如果我们需要其中一个大于另一个,那就需要两个线圈共地,那么两者的一端频率相等,另一端就会出现频率差异。比如一端选择标准的真空磁导率和介电常数,
具有虚数单位性质,它和它自己的负倒数相等,所以两种不同的真空磁导率的比值和比值的倒数相等。这就说明两种真空磁导率是同时存在的。可以通过调节电流电压和频率来使得它发生变化。但如果我们需要其中一个大于另一个,那就需要两个线圈共地,那么两者的一端频率相等,另一端就会出现频率差异。比如一端选择标准的真空磁导率和介电常数,
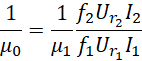
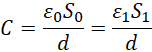
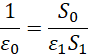
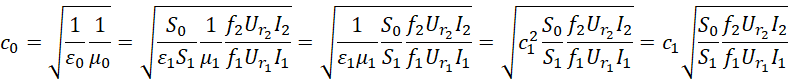
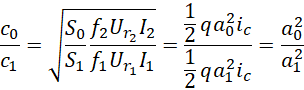
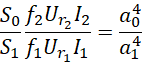
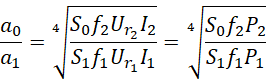
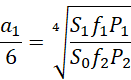
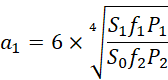
这样就可以换掉首项,进入其它平行世界。再回来观察,
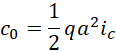
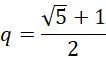
![]()
首项,
![]()
斐波那契数列的前四项就是,
![]()
所以2和3并不是最前面的两个质数,而是斐波那契数列的前四项(包括两个1),
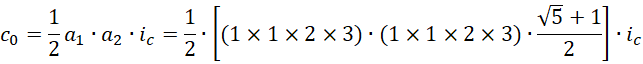
也就是说可以认为![]() 内部包含两个相互垂直或者首尾相接的斐波那契数列。较为基础的数列的头四项是较为高级的数列的单位。因为黄金分割率是斐波那契数列的极限两项之间的比率,所以这里表示的是较高级的数列的极限两项是基础数列的最初四项的乘积。或者说,当前数列的最后两项的单位是另一个斐波那契数列的最初四项的乘积(其中最前面的两项为1)。如果2和3是质数,那就会无法构成斐波那契数列的递归关系,所以应当认为2和3的出现不是因为它们是质数。另外除了2和3之外,没有两个质数是相邻的。好在我们求得的结果,
内部包含两个相互垂直或者首尾相接的斐波那契数列。较为基础的数列的头四项是较为高级的数列的单位。因为黄金分割率是斐波那契数列的极限两项之间的比率,所以这里表示的是较高级的数列的极限两项是基础数列的最初四项的乘积。或者说,当前数列的最后两项的单位是另一个斐波那契数列的最初四项的乘积(其中最前面的两项为1)。如果2和3是质数,那就会无法构成斐波那契数列的递归关系,所以应当认为2和3的出现不是因为它们是质数。另外除了2和3之外,没有两个质数是相邻的。好在我们求得的结果,
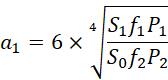
并不要求![]() 必须是质数的乘积。综合一下,斐波那契数列,
必须是质数的乘积。综合一下,斐波那契数列,
![]()
![]()
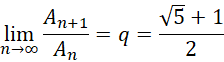
![]()
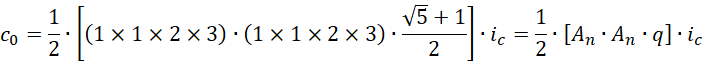
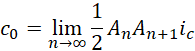
显然我们要的 不是![]() 无穷多项中的最后一项,而是其中的某一项,
无穷多项中的最后一项,而是其中的某一项,
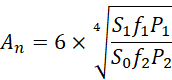
它应当符合斐波那契数列中的连续四项的乘积,因为开头两项是1,所以可以移位两项,也是成立的。从这个角度来看,
![]()
中的正弦函数和余弦函数的周期性,实际上来自于斐波那契数列。从其可移动相位来看,直接符合斐波那契数列的是余弦函数。
所以并非任何面积,频率或者功率都可以满足,
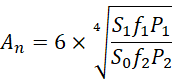
需要![]() 是斐波那契数列数列的连续四项的乘积。但是哪怕稍微移相,四个数的乘积都会非常大,比如移动半个周期,
是斐波那契数列数列的连续四项的乘积。但是哪怕稍微移相,四个数的乘积都会非常大,比如移动半个周期,
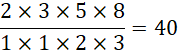
就会增大40倍,再移动半个周期,
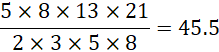
增大45倍,如果移动一个周期,

则增大1820倍。所以若要提升![]() 可以遵循半周期提升的方法。假定提升一个周期之后,单位会归1,那么提升一个周期之后,斐波那契数列的前4个数仍然可以被认为是1,1,2,3。只是这里的1,已经相当于原来的1840。
可以遵循半周期提升的方法。假定提升一个周期之后,单位会归1,那么提升一个周期之后,斐波那契数列的前4个数仍然可以被认为是1,1,2,3。只是这里的1,已经相当于原来的1840。
显然可以通过这种方式不断向上爬升,
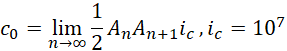
每个周期都可以提升,
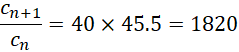
倍,综合结果为,
![]()
但相对于自身来说始终不变。由于光速可以近乎无限的增大,两点之间的距离就相当于可以无限缩短,所以从无限角度来说,宇宙中的任意两点都是没有距离的。
再看,
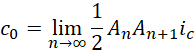
假定![]() 到
到![]() 为线性增长,选取中间值,
为线性增长,选取中间值,
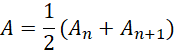
替换两端的值,
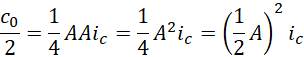
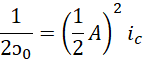
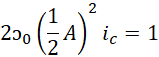
![]()
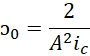
光速倒写的数值越小,速度速度越快,或者说等时间前提下,两点之间的距离越短,因为此时的时间就是距离。再以米秒制写出,
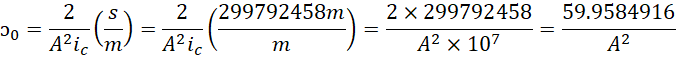
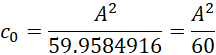
此处给出的是给定A也就是四个相邻的斐波那契数的前提下,标准1米的长度相当于多少米的长度。
带入层次n,得到关于n的函数,
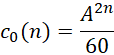
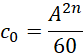
比如,
![]()
![]()
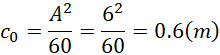
这个长度短于1米,但如果,
![]()
![]()
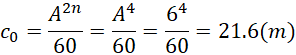
也就是1米长度相当于21.6米;如果,
![]()
![]()
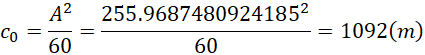
也就是1米的长度相当于1092米,或者,
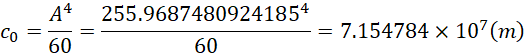
1米的长度相当于七千万米,这样的话两点之间的距离就被严重的缩短了。实际的情况很可能是斐波那契数列中只有两项两项的出现,而不是四项四项的出现,所以一个周期的压缩比率可能不会太高。
经过这些讨论,我们要问的是,真空中的标准光速![]() 是可变的吗?从其常数特性来看,它是不可变的,
是可变的吗?从其常数特性来看,它是不可变的,
但是作为绝对速度,由真空磁导率和真空介电常数构成,它是可变的,也是可调的。对这个数量进行调节,就可以获得不同的长度和时间的比例关系,进而实现拉长或者缩短时空的效果。
然后考虑万有引力常数,
![]()
得到单位为秒的平方的结果,
![]()
把这个结果带入方程,得到电子在电子周围电子长度为半径处的引力加速度,
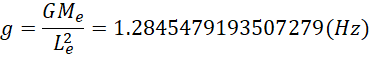
同理按照常规的物理方法计算,
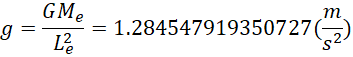
这两个数值近似相等,可以推导单位,
![]()
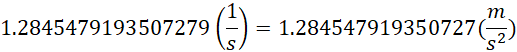
![]()
也就是说,万有引力常数G,是使得,
![]()
的换算单位。而光速是使得,
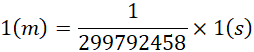
的换算单位。
![]()
它接近于,
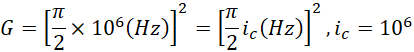
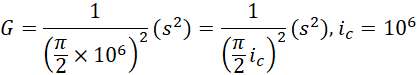
至于它难于量准确,主要是因为它涉及的跨度太大,从宏观到电子的数量级跨度![]() 大于虚数单位
大于虚数单位![]() 的数量级跨度。从数量上理解,最后考虑普朗克长度和普朗克时间,
的数量级跨度。从数量上理解,最后考虑普朗克长度和普朗克时间,
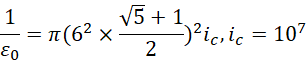
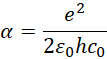
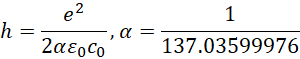
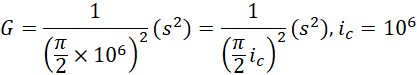
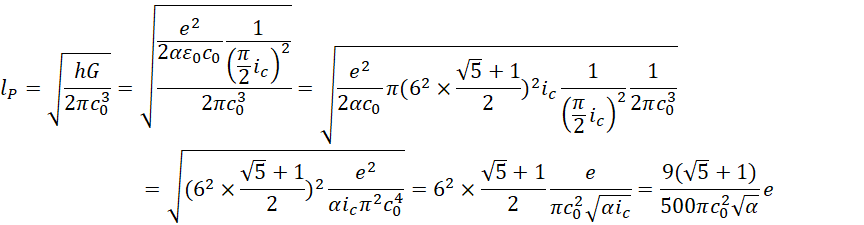
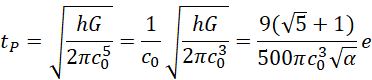
可见即便万有引力常数,光速和精细结构常数不变,普朗克长度和普朗克时间仍然是和电子的静止频率成正比的。
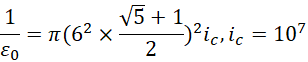
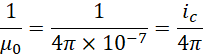
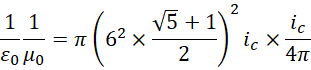
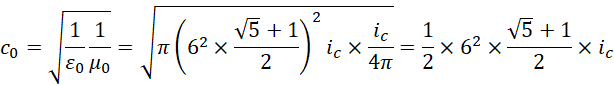
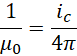
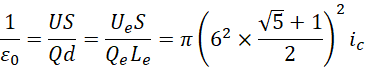
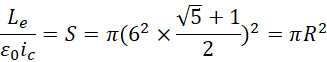
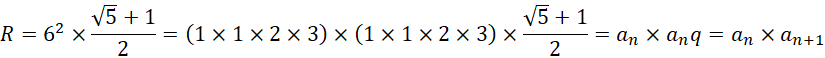
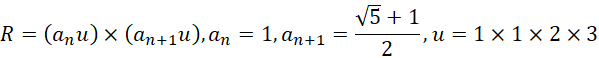
可见R仍然是一个二维结构,是一个长为1,宽为1.61803,单位为6的长方形,这就构成一个圆柱体,
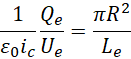
把![]() 理解为一种比例系数,则
理解为一种比例系数,则![]() 和
和![]() 具有同构性,
具有同构性,![]() 所描述的电子长度对应于
所描述的电子长度对应于![]() 所描述的电子长度,
所描述的电子长度,![]() 所描述的电子电量对应于
所描述的电子电量对应于![]() 所描述的电子电量,
所描述的电子电量,
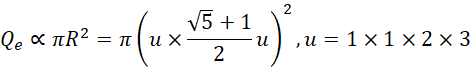
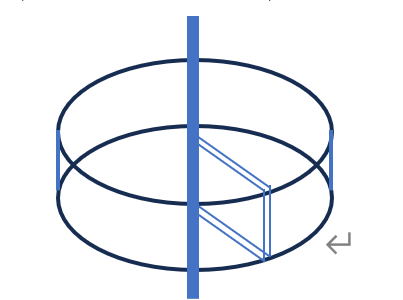
半径由一个长方体构成,长宽高分别为3,2,1,构成三维,第零维的点的大小也为1。
![]() 指的就是这种结构,圆柱体的3维体积,和电子长度的比值,从数值上放大
指的就是这种结构,圆柱体的3维体积,和电子长度的比值,从数值上放大![]() 倍。观察,
倍。观察,
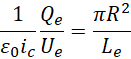
这个体现为一个圆面积的体积和某种特定(电子)长度的比值。结果得到一个二维面积,但这个二维面积的两个维数上的单位长度都是1。所以,方程右侧是一种面积而不是一种长度,
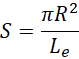
根据量纲分析,左侧为,
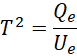
单位是秒的平方,所以,
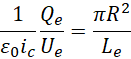
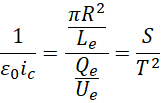
![]() 就是时间的平方转化到长度的平方也就是面积的比例系数。
就是时间的平方转化到长度的平方也就是面积的比例系数。![]() 就是这个比例系数放大
就是这个比例系数放大![]() 倍的结果。从体积比长度的角度理解,
倍的结果。从体积比长度的角度理解,
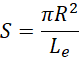
这个面积显然取决于长度,因为分子是不变的,分母是可变的电子的长度,而![]() 和
和![]() 也是随着电子的长度改变的。但是回顾,
也是随着电子的长度改变的。但是回顾,
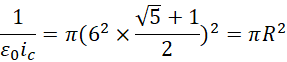
可见电子的长度和电量以及电压已经被三个物理量之间的关系内部处理了,
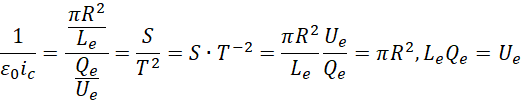
剩下的就是三维体积和一维长度的比值,内在的体积被认为是长度,最后得到长度的比率。而这个比率指的是外在度量电子的长度和内部结构上电子单位时间振动总量的比例关系。也就是说,
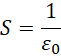
表示电子内外度量之间的比例关系的平方,而它配合纯数![]() ,相乘再开平方,
,相乘再开平方,
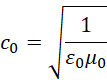
就是电子的内在长度度量结果和外在长度度量结果的比例关系。这个值对于常规电子来说,内在单位长度是6,外在单位长度是1。因为内在的长度无法度量,所以即便是面积或者体积,向外体现的仍然是长度,也就是说,内在的体积等于内在的面积等于对外体现的长度。外在的长度用时间来表示,而内在的长度用频率来表示。所以内在长度越高,频率越高,外在长度越高,频率越低。于是就有了提升频率也就是提升内在长度,进而可以改变内外长度比的方法。需要特别指出的是,方程,
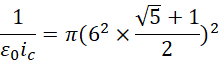
中的6是2和3的乘积,但也可以是-2和-3的乘积。也就是说,存在“负斐波那契数列”,
![]()
把-2和-3带入上述方程,结果是不可区分的。但是,对于光速来说,是有影响的,因为开方出来的两个-1,会复合到![]() 和
和![]() ,进而使得所描述的电子为相反的电子(可能是正电子)。因为负数本身相当于周期中非常大的数,从内在高频的角度理解,显然具有更高的频率,但是这个频率是不断下降的。
,进而使得所描述的电子为相反的电子(可能是正电子)。因为负数本身相当于周期中非常大的数,从内在高频的角度理解,显然具有更高的频率,但是这个频率是不断下降的。
