生成模型 | DDPM -> Imrpoved DDPM -> DDIM
DDPM: Denoising Diffusion Probabilistic Models

采样过程中的迭代计算为:
- xt−1=1αt(xt−1−αt1−αˉϵθ(xt,t))+β~tzx_{t-1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}}}\epsilon_{\theta}(x_t, t)) + \sqrt{\tilde{\beta}_t} zxt−1=αt1(xt−1−αˉ1−αtϵθ(xt,t))+β~tz
- z∼N(0,I)if t>1else z=0z \sim N(0, I) \, \text{ if } t > 1 \, \text{ else } \, z = 0z∼N(0,I) if t>1 else z=0
对应于前面的介绍:
- μ~θ(xt,t)=1αt(xt−1−αt1−αˉϵθ(xt,t))\tilde{\mu}_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}}}\epsilon_{\theta}(x_t, t))μ~θ(xt,t)=αt1(xt−1−αˉ1−αtϵθ(xt,t)):由于训练过程中 xtx_txt 是已知的,所以直接使用模型预测其中的噪声即可。
- β~θ(xt,t)=β~tI\tilde{\beta}_\theta(x_t, t) = \tilde{\beta}_t Iβ~θ(xt,t)=β~tI:而这里的方差既可以学习获得,也可以手工设置。DDPM使用后者,因为发现训练一个对角方差βθ\beta_\thetaβθ会导致训练不稳定且采样质量较差。不考虑其训练的话,可以通过移除常数项从而简化损失函数中间项 (1≤t<T1\le t < T1≤t<T) 为LsimpleL_\text{simple}Lsimple,通常设置采样中的方案 β~t=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_tβ~t=1−αˉt1−αˉt−1⋅βt(fixedsmall,即前述推导所得的形式)或者直接设置为前向方差 βt\beta_tβt(fixedlarge,要大于fixedsmall,αˉt<αˉt−1\bar{\alpha}_t < \bar{\alpha}_{t-1}αˉt<αˉt−1)。
所以损失函数为:
Lsimple=Eq(x0:T)[∥ϵt−ϵθ(xt,t)∥2]=Eq(x0:T)[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]L^\text{simple} = \mathbb{E}_{q(x_{0:T})} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] = \mathbb{E}_{q(x_{0:T})} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] Lsimple=Eq(x0:T)[∥ϵt−ϵθ(xt,t)∥2]=Eq(x0:T)[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]
- T=1000T = 1000T=1000:预设的步数。
- αt=1−0.02tT⇒logαˉt=∑t=1Tlog(1−0.02tT)<∑t=1T−0.02tT=−0.02TT(T+1)2=−0.01(T+1)=−10.01⇒αˉt≤e−10.01≈0\alpha_t = 1 - \frac{0.02t}{T} \Rightarrow \log \bar{\alpha}_t = \sum_{t=1}^{T} \log(1 - \frac{0.02t}{T}) < \sum_{t=1}^{T} - \frac{0.02t}{T} = - \frac{0.02}{T}\frac{T(T+1)}{2} = -0.01(T+1) = -10.01 \Rightarrow \bar{\alpha}_t \le e^{-10.01} \approx 0αt=1−T0.02t⇒logαˉt=∑t=1Tlog(1−T0.02t)<∑t=1T−T0.02t=−T0.022T(T+1)=−0.01(T+1)=−10.01⇒αˉt≤e−10.01≈0,从而可以将数据抑制为仅剩噪声。注意这里使用了不等式关系x1+x≤log(1+x)≤x,∀x>−1\frac{x}{1+x} \le \log(1+x) \le x, \forall x > -11+xx≤log(1+x)≤x,∀x>−1。
- 对应的β1=2×10−5→βT=0.02\beta_1 = 2 \times 10^{-5} \rightarrow \beta_T = 0.02β1=2×10−5→βT=0.02的线性插值。
按照反向扩散过程的马尔可夫链从DDPM生成样本是非常慢的,因为这里的TTT可能上达数千步。所以后续许多方法对其采样过程进行了优化与调整,来实现更快的图像生成。
Improved DDPM: Improved Denoising Diffusion Probabilistic Models
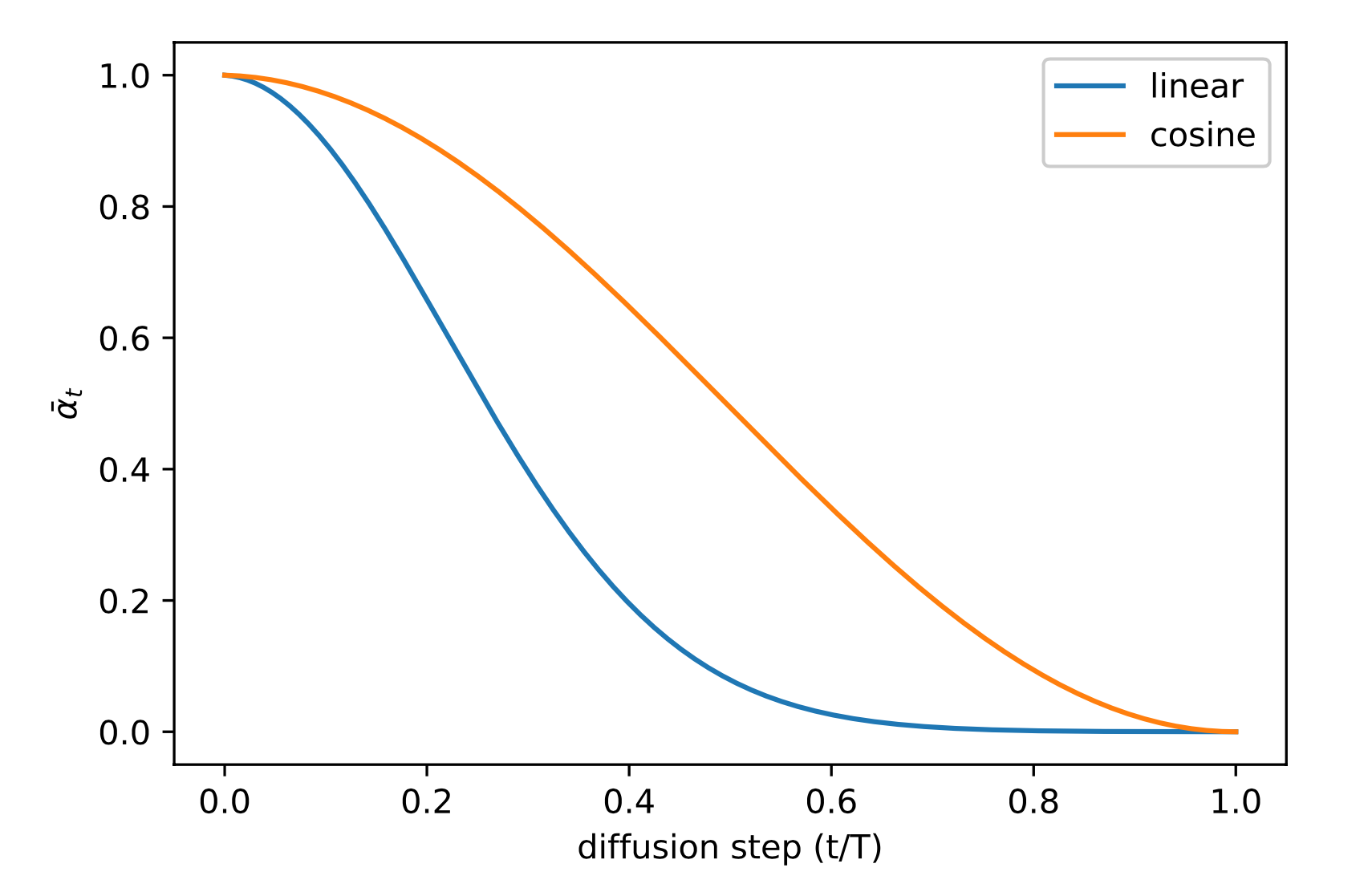
- βt\beta_tβt:相较于DDPM中使用的线性常量增加的序列,使用了基于余弦形式的调整策略。调度函数的选择可以是任意的,只要它在训练过程的中间提供一个近似线性的下降,并在t=0t=0t=0和t=Tt=Tt=T附近有微小的变化。这里使用的是:βt=clip(1−αˉtαˉt−1,0.999),αˉt=f(t)f(0),where f(t)=cos(t/T+s1+s⋅π2)2\beta_t=\text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999), \, \bar{\alpha}_t=\frac{f(t)}{f(0)}, \, \text{where } f(t)=\cos(\frac{t/T + s}{1 + s} \cdot \frac{\pi}{2})^2βt=clip(1−αˉt−1αˉt,0.999),αˉt=f(0)f(t),where f(t)=cos(1+st/T+s⋅2π)2,这里的sss是一个超参数,用于控制t=0t=0t=0时的噪声尺度。
- β~θ(xt,t)=exp(vlogβt+(1−v)logβ~t)\tilde{\beta}_\theta(x_t, t) = \exp(v \log \beta_t + (1-v) \log \tilde{\beta}_t)β~θ(xt,t)=exp(vlogβt+(1−v)logβ~t):利用模型预测两个边界值βt\beta_tβt和β~t\tilde{\beta}_tβ~t之间的混合向量vvv。相应的,DDPM中使用的简单版本的损失函数就没法使用了。所以使用了Lhybrid=Lsimple+λLVLB,λ=0.001L_{\text{hybrid}} = L_{\text{simple}} + \lambda L_{VLB}, \, \lambda=0.001Lhybrid=Lsimple+λLVLB,λ=0.001,这里的第二项中会截止μ~θ\tilde{\mu}_\thetaμ~θ的梯度,从而仅仅引导方差项的学习。经验观察到,由于有噪声梯度,优化起来很有挑战性,所以建议对第二项使用配合重要性采样的时间平均平滑版本。
为了加快采样过程,本文直接对原本完整的TTT步,使用⌈T/S⌉\lceil T/S \rceil⌈T/S⌉作为采样步间隔得到新的采样步{τ1,…,τS}\{\tau_1, \dots, \tau_S\}{τ1,…,τS},从而将整体步数缩减为SSS步。
DDIM: Denoising Diffusion Implicit Models
DDPM 的损失函数尽管在推导中依赖马尔可夫性,但是最终形式却只依赖边际分布q(xt∣x0)q(x_t | x_0)q(xt∣x0),所有出现的 q(⋅∣x0)q(\cdot | x_0)q(⋅∣x0) 都是由 αˉt\bar{\alpha}_tαˉt 定义的边际高斯分布,而这些边际分布的形式在任何满足相同边际的前向过程(无论是马尔可夫还是非马尔可夫)下都保持不变。DDIM 中通过延续这些边际分布,但是将原来 DDPM 的马尔可夫链换成一条非马尔可夫链,从而设计为更有效的迭代隐式概率模型。其本身由于边际分布不变,所以损失形式可以沿用DDPM的形式,具有相同的训练目标。但其反向过程(去噪生成过程)却因为忽略了马尔可夫性,使其避免了相邻步之间的依赖,从而可以更快地采样。
非马尔科夫链采样
DDPM依据马尔可夫链性质,对反向转移分布q(xt−1∣xt,x0)q(x_{t-1} | x_t, x_0)q(xt−1∣xt,x0)进行了简化和拆解,最终得到了如下形式:
q(xt−1∣xt,x0)=N(μ~t(xt,x0),β~tI)=N(αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0,1−αˉt−11−αˉtβtI)\begin{align} q(x_{t-1} | x_t, x_0) = \mathcal{N}(\tilde{\mu}_t(x_t, x_0), \tilde{\beta}_t I) = \mathcal{N}(\frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1-\bar{\alpha}_{t}} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t} }{1 - \bar{\alpha}_{t}} x_{0}, \frac{1 - \bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}} \beta_{t} I) \end{align} q(xt−1∣xt,x0)=N(μ~t(xt,x0),β~tI)=N(1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0,1−αˉt1−αˉt−1βtI)
这份工作直接假定了非马尔可夫链条件下的情况:
q(xt−1∣xt,x0)=N(kx0+mxt,β^tI)自定义了均值和方差q(xt−1∣x0)=N(αˉt−1x0,(1−αˉt−1)I)xt−1=kx0+mxt+β^tϵϵ∼N(0,I)=kx0+m(αˉtx0+1−αˉtϵˉt)+β^tϵϵˉt∼N(0,I)=(k+mαˉt)x0+m1−αˉtϵˉt+β^tϵ=(k+mαˉt)x0+m2(1−αˉt)+β^tϵ′ϵ′∼N(0,I)⇓结合前述分布形式⇒{k+mαˉt=αˉt−1m2(1−αˉt)+β^t=1−αˉt−1⇒{k=αˉt−1−αˉt1−αˉt−1−β^t1−αˉtm=1−αˉt−1−β^t1−αˉt⇓q(xt−1∣xt,x0)=N((αˉt−1−αˉt1−αˉt−1−β^t1−αˉt)x0+(1−αˉt−1−β^t1−αˉt)xt,β^tI)=N(αˉt−1x0+1−αˉt−1−β^txt−αˉtx01−αˉt,β^tI)xt−1=αˉt−1x0+1−αˉt−1−β^txt−αˉtx01−αˉt+β^tϵ′=αˉt−1(xt−1−αˉtϵˉθ(xt,t)αˉt)+1−αˉt−1−β^txt−(xt−1−αˉtϵˉθ(xt,t))1−αˉt+β^tϵ′=αˉt−1(xt−1−αˉtϵˉθ(xt,t)αˉt)⏟predicted x0+1−αˉt−1−β^tϵˉθ(xt,t)⏟direction pointing to xt+β^tϵ′⏟random noise\begin{align} q(x_{t-1} | x_t, x_0) & = \mathcal{N}(k x_0 + m x_t, \hat{\beta}_t I) & \text{自定义了均值和方差} \\ q(x_{t-1} | x_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_{t-1}} x_0, (1 - \bar{\alpha}_{t-1}) \mathbf{I}) \\ x_{t-1} & = k x_0 + m x_t + \sqrt{\hat{\beta}_t} \epsilon & \epsilon \sim \mathcal{N}(0, I) \\ & = k x_0 + m (\sqrt{\bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_t) + \sqrt{\hat{\beta}_t} \epsilon & \bar{\epsilon}_t \sim \mathcal{N}(0, I) \\ & = (k + m \sqrt{\bar{\alpha}_t}) x_0 + m \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_t + \sqrt{\hat{\beta}_t} \epsilon \\ & = (k + m \sqrt{\bar{\alpha}_t}) x_0 + \sqrt{m^2 (1 - \bar{\alpha}_t) + \hat{\beta}_t} \epsilon' & \epsilon' \sim \mathcal{N}(0, I) \\ \Downarrow \\ \text{结合前述分布形式} \Rightarrow & \begin{cases} k + m \sqrt{\bar{\alpha}_t} = \sqrt{\bar{\alpha}_{t-1}} \\ m^2 (1 - \bar{\alpha}_t) + \hat{\beta}_t = 1 - \bar{\alpha}_{t-1} \\ \end{cases} \Rightarrow \begin{cases} k = \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\bar{\alpha}_t} \sqrt{\frac{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t}{1 - \bar{\alpha}_{t}}} \\ m = \sqrt{\frac{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t}{1 - \bar{\alpha}_{t}}} \\ \end{cases} \\ \Downarrow \\ q(x_{t-1} | x_t, x_0) & = \mathcal{N}(\Big( \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\bar{\alpha}_t} \sqrt{\frac{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t}{1 - \bar{\alpha}_{t}}} \Big)x_0 + \Big( \sqrt{\frac{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t}{1 - \bar{\alpha}_{t}}} \Big) x_t, \hat{\beta}_t I) \\ & = \mathcal{N}(\sqrt{\bar{\alpha}_{t-1}} x_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \frac{x_t - \sqrt{\bar{\alpha}_t} x_0}{\sqrt{1 - \bar{\alpha}_{t}}}, \hat{\beta}_t I) \\ x_{t-1} & = \sqrt{\bar{\alpha}_{t-1}} x_0 + \sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \frac{x_t - \sqrt{\bar{\alpha}_t} x_0}{\sqrt{1 - \bar{\alpha}_{t}}} + \sqrt{\hat{\beta}_t} \epsilon' \\ & = \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \frac{x_t - (x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t))}{\sqrt{1 - \bar{\alpha}_{t}}} + \sqrt{\hat{\beta}_t} \epsilon' \\ & = \sqrt{\bar{\alpha}_{t-1}} \underbrace{\Big( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} \Big)}_{\text{predicted } x_0} + \underbrace{\sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \bar{\epsilon}_\theta(x_t, t)}_{\text{direction pointing to } x_t} + \underbrace{\sqrt{\hat{\beta}_t} \epsilon'}_\text{random noise} \\ \end{align} q(xt−1∣xt,x0)q(xt−1∣x0)xt−1⇓结合前述分布形式⇒⇓q(xt−1∣xt,x0)xt−1=N(kx0+mxt,β^tI)=N(αˉt−1x0,(1−αˉt−1)I)=kx0+mxt+β^tϵ=kx0+m(αˉtx0+1−αˉtϵˉt)+β^tϵ=(k+mαˉt)x0+m1−αˉtϵˉt+β^tϵ=(k+mαˉt)x0+m2(1−αˉt)+β^tϵ′{k+mαˉt=αˉt−1m2(1−αˉt)+β^t=1−αˉt−1⇒⎩⎨⎧k=αˉt−1−αˉt1−αˉt1−αˉt−1−β^tm=1−αˉt1−αˉt−1−β^t=N((αˉt−1−αˉt1−αˉt1−αˉt−1−β^t)x0+(1−αˉt1−αˉt−1−β^t)xt,β^tI)=N(αˉt−1x0+1−αˉt−1−β^t1−αˉtxt−αˉtx0,β^tI)=αˉt−1x0+1−αˉt−1−β^t1−αˉtxt−αˉtx0+β^tϵ′=αˉt−1(αˉtxt−1−αˉtϵˉθ(xt,t))+1−αˉt−1−β^t1−αˉtxt−(xt−1−αˉtϵˉθ(xt,t))+β^tϵ′=αˉt−1predicted x0(αˉtxt−1−αˉtϵˉθ(xt,t))+direction pointing to xt1−αˉt−1−β^tϵˉθ(xt,t)+random noiseβ^tϵ′自定义了均值和方差ϵ∼N(0,I)ϵˉt∼N(0,I)ϵ′∼N(0,I)
本文设置了一个特殊的方差:β^t\hat{\beta}_tβ^t,这里的η∈R+\eta \in \mathbb{R}^{+}η∈R+是一个超参数用于控制采样过程中的方差,从而调整过程的随机性。
β^t=η2β~t=η21−αˉt−11−αˉtβt=η21−αˉt−11−αˉt(1−αt)\begin{align} \hat{\beta}_t = \eta^2 \tilde{\beta}_t = \eta^2 \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t = \eta^2 \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} (1-\alpha_t) \end{align} β^t=η2β~t=η21−αˉt1−αˉt−1βt=η21−αˉt1−αˉt−1(1−αt)
由于推导过程中,并未使用马尔科夫链的特性,所以DDIM的q(xt−1∣xt,x0)q(x_{t-1} | x_t, x_0)q(xt−1∣xt,x0)实际上可以扩展为q(xτi−1∣xτt,x0)q(x_{\tau_{i-1}} \vert x_{\tau_t}, x_0)q(xτi−1∣xτt,x0),从而再生成过程中,只需要SSS个扩散步,即{τ1,…,τS}\{\tau_1, \dots, \tau_S\}{τ1,…,τS}:
q(xτi−1∣xτt,x0)=N(αˉτi−1x0+1−αˉτi−1−β^τixτi−αˉτix01−αˉτi,β^τiI)\begin{align} q(x_{\tau_{i-1}} \vert x_{\tau_t}, x_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_{\tau_{i}-1}}x_0 + \sqrt{1 - \bar{\alpha}_{\tau_{i}-1} - \hat{\beta}_{\tau_{i}}} \frac{x_{\tau_i} - \sqrt{\bar{\alpha}_{\tau_{i}}}{x}_0}{\sqrt{1 - \bar{\alpha}_{\tau_{i}}}}, \hat{\beta}_{\tau_{i}} \mathbf{I}) \\ \end{align} q(xτi−1∣xτt,x0)=N(αˉτi−1x0+1−αˉτi−1−β^τi1−αˉτixτi−αˉτix0,β^τiI)
这实际上也证明了,如过想要准确的估计出来q(xt−1∣xt,x0)q(x_{t-1} | x_t, x_0)q(xt−1∣xt,x0),实际上不是必须要计算q(xt∣xt+1,x0)q(x_t | x_{t+1}, x_0)q(xt∣xt+1,x0),而DDPM中的马尔科夫性质对相邻时间步是存在约束的。因此,模型只要在训练中能够学会如何估计出每步积累的噪声就好了,而没有必要在采样中每步一一执行。当然,这也进一步对模型的噪声估计提出了要求。步数越且步数分布比较合理时,效果越好。因为对于距离更近的步骤,通过网络预测出对应的噪声会更容易。
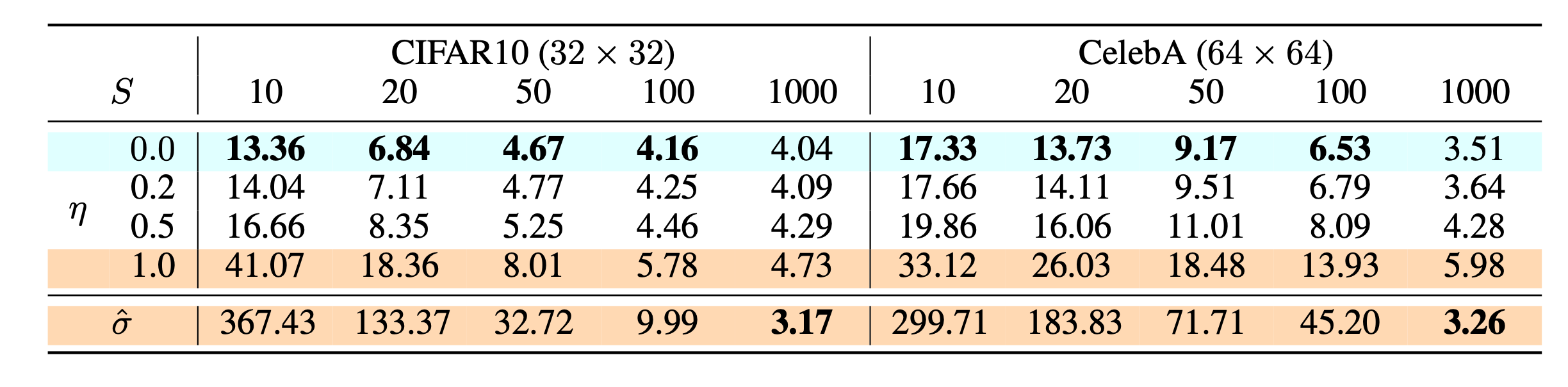
在设置T=1000T=1000T=1000时:
- 当选定的步数SSS很少时,例如η=0\eta = 0η=0的DDIM可以获得最好的生成质量,而η=1\eta = 1η=1时则差得多。
- 当选定的步数S=TS=TS=T时,使用更大的方差能够获得更好的效果。
方差构造
方差参数的三种特殊版本:
- η=1\eta = 1η=1:等价于DDPM的fixedsmall版本。
- η=0\eta = 0η=0:采样过程不再具有随机性。
- β^t=β~t=βt\hat{\beta}_t = \tilde{\beta}_t = \beta_tβ^t=β~t=βt:等价于DDPM的fixedlarge版本。
在生成过程中,这里的方差参数越小,最终生成图像的噪声和多样性反而相对来说越大;整体步数(跨步)越少,生成的图片更加平滑,多样性也会有所降低;所以在整体扩散部署减少的时候,可以适当缩小β^t\hat{\beta}_tβ^t,以保持生成图片质量大致不变,这跟DDIM原论文的实验结论是一致的。总体来说不带噪声的生成过程的生成效果不如带噪声的生成过程,不带噪声时生成效果受模型架构影响较大。
η=1\eta=1η=1 等价于DDPM
此时DDPM和DDIM的优化目标q(xt−1∣xt,x0)q(x_{t-1} | x_t, x_0)q(xt−1∣xt,x0)就一样了,此时二者的方差是一样的,对于均值,可以进行如下推导:
αˉt−1(xt−1−αˉtϵˉθ(xt,t)αˉt)+1−αˉt−1−β^tϵˉθ(xt,t)=αˉt−1αˉt(xt−1−αˉtϵˉθ(xt,t))+1−αˉt−1−1−αˉt−11−αˉt(1−αt)ϵˉθ(xt,t)=1αtxt−1−αˉtαtϵˉθ(xt,t)+(αt−αˉt)(1−αˉt−1)1−αˉtϵˉθ(xt,t)=1αtxt−1−αˉtαtϵˉθ(xt,t)+αt(1−αˉt−1)21−αˉtϵˉθ(xt,t)=1αtxt−1−αˉtαtϵˉθ(xt,t)+(1−αˉt−1)αt1−αˉtϵˉθ(xt,t)=1αtxt+((1−αˉt−1)αt1−αˉt−1−αˉtαt)ϵˉθ(xt,t)=1αt(xt+(1−αˉt−1)αt−(1−αˉt)1−αˉtϵˉθ(xt,t))=1αt(xt+αt−αˉt−1+αˉt1−αˉtϵˉθ(xt,t))=1αt(xt−1−αt1−αˉtϵˉθ(xt,t))=1αt(xt−βt1−αˉtϵˉθ(xt,t))\begin{align} \sqrt{\bar{\alpha}_{t-1}} \Big( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} \Big) & + \sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{\sqrt{\bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_t}} \Big( x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t) \Big) + \sqrt{1 - \bar{\alpha}_{t-1} - \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} (1-\alpha_t)} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\alpha_t}} \bar{\epsilon}_\theta(x_t, t) + \sqrt{\frac{(\alpha_t - \bar{\alpha}_t) (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\alpha_t}} \bar{\epsilon}_\theta(x_t, t) + \sqrt{\frac{\alpha_t (1 - \bar{\alpha}_{t-1})^2}{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} x_t - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\alpha_t}} \bar{\epsilon}_\theta(x_t, t) + (1 - \bar{\alpha}_{t-1})\sqrt{\frac{\alpha_t }{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} x_t + \Big( (1 - \bar{\alpha}_{t-1})\frac{\sqrt{\alpha_t}}{\sqrt{1 - \bar{\alpha}_t}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\alpha_t}} \Big) \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} \Big( x_t + \frac{(1 - \bar{\alpha}_{t-1}) \alpha_t - (1 - \bar{\alpha}_t)}{\sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \Big) \\ & = \frac{1}{\sqrt{\alpha_t}} \Big( x_t + \frac{\alpha_t - \bar{\alpha}_{t} - 1 + \bar{\alpha}_t}{\sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \Big) \\ & = \frac{1}{\sqrt{\alpha_t}} \Big( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \Big) \\ & = \frac{1}{\sqrt{\alpha_t}} \Big( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) \Big) \\ \end{align} αˉt−1(αˉtxt−1−αˉtϵˉθ(xt,t))+1−αˉt−1−β^tϵˉθ(xt,t)=αˉtαˉt−1(xt−1−αˉtϵˉθ(xt,t))+1−αˉt−1−1−αˉt1−αˉt−1(1−αt)ϵˉθ(xt,t)=αt1xt−αt1−αˉtϵˉθ(xt,t)+1−αˉt(αt−αˉt)(1−αˉt−1)ϵˉθ(xt,t)=αt1xt−αt1−αˉtϵˉθ(xt,t)+1−αˉtαt(1−αˉt−1)2ϵˉθ(xt,t)=αt1xt−αt1−αˉtϵˉθ(xt,t)+(1−αˉt−1)1−αˉtαtϵˉθ(xt,t)=αt1xt+((1−αˉt−1)1−αˉtαt−αt1−αˉt)ϵˉθ(xt,t)=αt1(xt+1−αˉt(1−αˉt−1)αt−(1−αˉt)ϵˉθ(xt,t))=αt1(xt+1−αˉtαt−αˉt−1+αˉtϵˉθ(xt,t))=αt1(xt−1−αˉt1−αtϵˉθ(xt,t))=αt1(xt−1−αˉtβtϵˉθ(xt,t))
微分方程视角
αtxt−1=xt−βt1−αˉtϵˉθ(xt,t)+αt1−αˉt−11−αˉt(1−αt)ϵ′xt−1αˉt−1=xtαˉt−1−αtαˉt1−αˉtϵˉθ(xt,t)+1−αˉt−1αˉt−11−αˉt(1−αt)ϵ′xtαˉt−xt−1αˉt−1=1−αtαˉt1−αˉtϵˉθ(xt,t)−1−αˉt−1αˉt−11−αˉt(1−αt)ϵ′⇓当T足够大,或两个α差异足够小(差异也小)Δ(x(s)αˉ(s))=1−α(s)⏞≈Δsαˉs1−αˉ(s)ϵˉθ(x(s),s)−1−αˉ(s−1)αˉ(s−1)1−αˉ(s)1−α(s)⏞≈Δsϵ′≈1αˉs1−αˉ(s)ϵˉθ(x(s),s)⏟drift itemΔs−1αˉ(s)⏟diffusion itemΔWs\begin{align} \sqrt{\alpha_t} x_{t-1} & = x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) + \sqrt{\alpha_t} \sqrt{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} } (1-\alpha_t) \epsilon' \\ \frac{x_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} & = \frac{x_{t}}{\sqrt{\bar{\alpha}_{t}}} - \frac{1 - \alpha_t}{\sqrt{\bar{\alpha}_{t}} \sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) + \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}} \sqrt{1 - \bar{\alpha}_t}} \sqrt{(1-\alpha_t)} \epsilon' \\ \frac{x_{t}}{\sqrt{\bar{\alpha}_{t}}} - \frac{x_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} & = \frac{1 - \alpha_t}{\sqrt{\bar{\alpha}_{t}} \sqrt{1 - \bar{\alpha}_t}} \bar{\epsilon}_\theta(x_t, t) - \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}} \sqrt{1 - \bar{\alpha}_t}} \sqrt{(1-\alpha_t)} \epsilon' \\ & \Downarrow 当T足够大,或两个\alpha差异足够小(差异也小)\\ \Delta \Big(\frac{x(s)}{\sqrt{\bar{\alpha}(s)}}\Big) & = \frac{\overbrace{1 - \alpha(s)}^{\approx \Delta_s}}{\sqrt{\bar{\alpha}_{s}} \sqrt{1 - \bar{\alpha}(s)}} \bar{\epsilon}_\theta(x(s), s) - \frac{\sqrt{1 - \bar{\alpha}(s-1)}}{\sqrt{\bar{\alpha}(s-1)} \sqrt{1 - \bar{\alpha}(s)}} \overbrace{\sqrt{1-\alpha(s)}}^{\approx \sqrt{\Delta_s}} \epsilon' \\ & \approx \underbrace{\frac{1}{\sqrt{\bar{\alpha}_{s}} \sqrt{1 - \bar{\alpha}(s)}} \bar{\epsilon}_\theta(x(s), s)}_\text{drift item} \Delta_s \underbrace{- \frac{1}{\sqrt{\bar{\alpha}(s)}}}_\text{diffusion item} \Delta_{W_s} \\ \end{align} αtxt−1αˉt−1xt−1αˉtxt−αˉt−1xt−1Δ(αˉ(s)x(s))=xt−1−αˉtβtϵˉθ(xt,t)+αt1−αˉt1−αˉt−1(1−αt)ϵ′=αˉtxt−αˉt1−αˉt1−αtϵˉθ(xt,t)+αˉt−11−αˉt1−αˉt−1(1−αt)ϵ′=αˉt1−αˉt1−αtϵˉθ(xt,t)−αˉt−11−αˉt1−αˉt−1(1−αt)ϵ′⇓当T足够大,或两个α差异足够小(差异也小)=αˉs1−αˉ(s)1−α(s)≈Δsϵˉθ(x(s),s)−αˉ(s−1)1−αˉ(s)1−αˉ(s−1)1−α(s)≈Δsϵ′≈drift itemαˉs1−αˉ(s)1ϵˉθ(x(s),s)Δsdiffusion item−αˉ(s)1ΔWs
这里的WsW_sWs表示维纳过程,其增量服从高斯分布ΔWs=Ws+Δs−Ws∼N(0,Δs)\Delta_{W_s} = W_{s + \Delta_s} - W_s \sim \mathcal{N}(0, \Delta_s)ΔWs=Ws+Δs−Ws∼N(0,Δs)
η=0\eta=0η=0 此时为确定性采样
此时β^t=0\hat{\beta}_t = 0β^t=0:
xt−1=αˉt−1(xt−1−αˉtϵˉθ(xt,t)αˉt)⏟predicted x0+1−αˉt−1−β^tϵˉθ(xt,t)⏟direction pointing to xt+β^tϵ′⏟random noise=αˉt−1xt−1−αˉtϵˉθ(xt,t)αˉt+1−αˉt−1ϵˉθ(xt,t)=xt−1−αˉtϵˉθ(xt,t)αt+1−αˉt−1ϵˉθ(xt,t)=1αtxt+(1−αˉt−1−1−αˉtαt)ϵˉθ(xt,t)\begin{align} x_{t-1} & = \sqrt{\bar{\alpha}_{t-1}} \underbrace{\Big( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} \Big)}_{\text{predicted } x_0} + \underbrace{\sqrt{1 - \bar{\alpha}_{t-1} - \hat{\beta}_t} \bar{\epsilon}_\theta(x_t, t)}_{\text{direction pointing to } x_t} + \underbrace{\sqrt{\hat{\beta}_t} \epsilon'}_\text{random noise} \\ & = \sqrt{\bar{\alpha}_{t-1}} \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\bar{\alpha}_t}} + \sqrt{1 - \bar{\alpha}_{t-1}} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \bar{\epsilon}_\theta(x_t, t)}{\sqrt{\alpha_t}} + \sqrt{1 - \bar{\alpha}_{t-1}} \bar{\epsilon}_\theta(x_t, t) \\ & = \frac{1}{\sqrt{\alpha_t}} x_t + \Big( \sqrt{1 - \bar{\alpha}_{t-1}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\alpha_t}} \Big) \bar{\epsilon}_\theta(x_t, t) \\ \end{align} xt−1=αˉt−1predicted x0(αˉtxt−1−αˉtϵˉθ(xt,t))+direction pointing to xt1−αˉt−1−β^tϵˉθ(xt,t)+random noiseβ^tϵ′=αˉt−1αˉtxt−1−αˉtϵˉθ(xt,t)+1−αˉt−1ϵˉθ(xt,t)=αtxt−1−αˉtϵˉθ(xt,t)+1−αˉt−1ϵˉθ(xt,t)=αt1xt+(1−αˉt−1−αt1−αˉt)ϵˉθ(xt,t)
此时采样过程不再依赖于外部新添加的噪声,而是仅仅依赖于模型预测的“确定”噪声。所以整体的预测过程就是完全确定的,意味着给定xtx_txt,得到的xt−1x_{t-1}xt−1就是唯一确定的。
微分方程视角
对前述公式进行进一步变换:
xt=αtxt−1−(αt1−αˉt−1−1−αˉt)ϵˉθ(xt,t)xtαˉt=αtαˉtxt−1−(αtαˉt1−αˉt−1−1−αˉtαˉt)ϵˉθ(xt,t)xtαˉt=xt−1αˉt−1−(1−αˉt−1αˉt−1−1−αˉtαˉt)ϵˉθ(xt,t)xtαˉt−xt−1αˉt−1=(1−αˉtαˉt−1−αˉt−1αˉt−1)ϵˉθ(xt,t)⇓当T足够大,或两个α足够小(差异也小)dds(x(s)αˉ(s))=ϵˉθ(x(s),t(s))dds(1−αˉ(s)αˉ(s))\begin{align} x_t & = \sqrt{\alpha_t} x_{t-1} - \Big( \sqrt{\alpha_t} \sqrt{1 - \bar{\alpha}_{t-1}} - \sqrt{1 - \bar{\alpha}_t} \Big) \bar{\epsilon}_\theta(x_t, t) \\ \frac{x_t}{\sqrt{\bar{\alpha}_t}} & = \frac{\sqrt{\alpha_t}}{\sqrt{\bar{\alpha}_t}} x_{t-1} - \Big( \frac{\sqrt{\alpha_t}}{\sqrt{\bar{\alpha}_t}} \sqrt{1 - \bar{\alpha}_{t-1}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} \Big) \bar{\epsilon}_\theta(x_t, t) \\ \frac{x_t}{\sqrt{\bar{\alpha}_t}} & = \frac{x_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} - \Big( \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}}} - \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} \Big) \bar{\epsilon}_\theta(x_t, t) \\ \frac{x_t}{\sqrt{\bar{\alpha}_t}} - \frac{x_{t-1}}{\sqrt{\bar{\alpha}_{t-1}}} & = \Big( \frac{\sqrt{1 - \bar{\alpha}_t}}{\sqrt{\bar{\alpha}_t}} - \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{\bar{\alpha}_{t-1}}} \Big) \bar{\epsilon}_\theta(x_t, t) \\ & \Downarrow 当T足够大,或两个\alpha足够小(差异也小)\\ \frac{d}{ds}\Big(\frac{x(s)}{\sqrt{\bar{\alpha}(s)}}\Big) & = \bar{\epsilon}_\theta(x(s), t(s)) \frac{d}{ds} \Big( \frac{\sqrt{1 - \bar{\alpha}(s)}}{\sqrt{\bar{\alpha}(s)}} \Big) \end{align} xtαˉtxtαˉtxtαˉtxt−αˉt−1xt−1dsd(αˉ(s)x(s))=αtxt−1−(αt1−αˉt−1−1−αˉt)ϵˉθ(xt,t)=αˉtαtxt−1−(αˉtαt1−αˉt−1−αˉt1−αˉt)ϵˉθ(xt,t)=αˉt−1xt−1−(αˉt−11−αˉt−1−αˉt1−αˉt)ϵˉθ(xt,t)=(αˉt1−αˉt−αˉt−11−αˉt−1)ϵˉθ(xt,t)⇓当T足够大,或两个α足够小(差异也小)=ϵˉθ(x(s),t(s))dsd(αˉ(s)1−αˉ(s))
基于这个常微分方程的视角,整体的采样过程就是从s=1(t=T)s=1 (t=T)s=1(t=T)求解s=0(t=0)s=0 (t=0)s=0(t=0)时的x(0)x(0)x(0)。而DDIM的这种确定性迭代过程,实际上对应了该常微分方程的欧拉解法。同样可以应用其他更有效的求解方案,例如R-K方案等。在这个视角下,生成过程等同于求解常微分方程,也因此可以进一步借助常微分方程的数值解法,为生成过程的加速提供更丰富多样的手段。
参考资料
- 万字长文【Diffusion Model-DDIM数学原理推导】与【源码详解】 - Dezeming的文章 - 知乎 https://zhuanlan.zhihu.com/p/1927489312892629561
- 生成扩散模型漫谈(四):DDIM = 高观点DDPM https://spaces.ac.cn/archives/9181
