当前位置： 首页 > news >正文

数学建模（摸索中……）

news 2025/8/25 8:32:46

目录

还在犹豫要不要报名数学建模大赛，目前在B站上面上课了一段时间感觉还是有很多不会的，按照这个大佬的讲解可以分成下面几个部分，通过自己记录看会不会效果好一点。

【胎教级入门数学建模】持续更新！可能是B站大学最良心的数学建模课程了，包含全套数学模型、算法、编程、写作、MATLAB教学视频_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1p14y1U7Nr/?spm_id_from=333.1007.0.0&vd_source=7c3bfbf39d037fe80c97234396acc524

层次分析法

一、数学建模层次分析法（AHP）【清风数学建模个人笔记】_ahp层次分析法-CSDN博客https://blog.csdn.net/m0_58882109/article/details/122483183?ops_request_misc=elastic_search_misc&request_id=6d4261a907b2c35ed550e477a67ee8b3&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-122483183-null-null.142^v102^pc_search_result_base3&utm_term=%E5%B1%82%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95&spm=1018.2226.3001.4187

概念

将主观判断进行量化，通过一套严谨的数学方法，最终帮你得出一个综合性的最优选择。

核心步骤

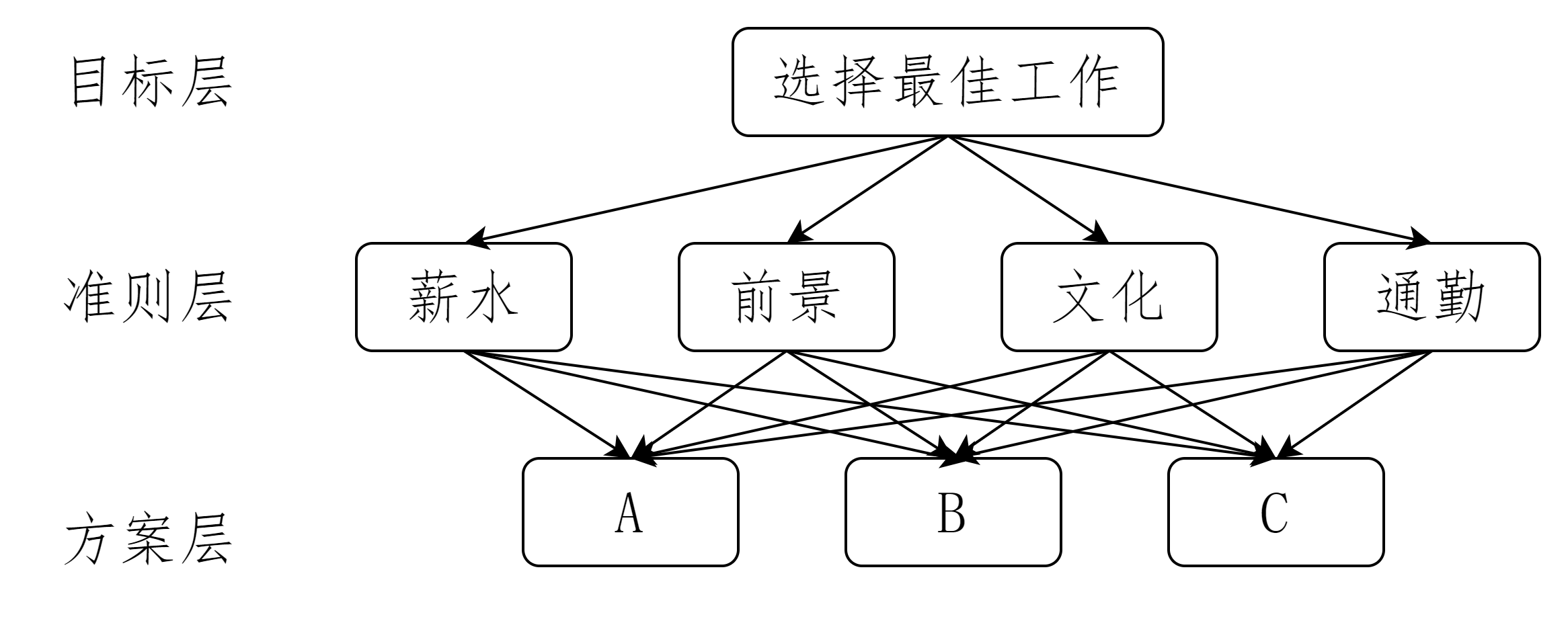
1.建立层次结构

  • 目标层
  • 准则层
  • 方案层

2.构造判断矩阵（核心步骤）

两两比较，比较准则的重要性（确定评价指标的权重），然后根据评价指标，在每个准则下比较方案。

3.层次单排序与一致性检验

用数学的方法从每个判断矩阵中算出权重（特征值法和算术平均值法），同时检查判断是否自相矛盾（因为在构造判断矩阵的时候进行的是两两比较，所以就可能出现逻辑混乱的情况）。

一致性指标 CI = (λ_max - n) / (n - 1)，一致性比例 CR = CI / RI。如果 CR < 0.1，则认为判断合理。

4.层次总排序

将所有权重组合起来。

示例

现在有一个这样的场景，需要你要从三个offer中选择一个工作（A, B, C公司）。 你该怎么做出一个不让自己后悔的决定呢？

建立层次结构

假设（这个实际需要查阅文献来进行比较重要程度）：

  • 准则：薪水、前景、文化、通勤

  • 方案：A公司、B公司、C公司

  • 你的主观判断：

    • 准则比较：前景 > 薪水 > 文化 > 通勤

    • 薪水比较：A > C > B

    • 前景比较：B > C > A

    • 文化比较：C > B > A

    • 通勤比较：A > B > C

比较准则的重要性（构建判断矩阵）

% 准则顺序：1薪水, 2前景, 3文化, 4通勤
CriteriaMatrix = [1,  1/3, 3,    5;    % 薪水 vs [薪水,前景,文化,通勤]3,  1,   5,    7;    % 前景 vs ...1/3,1/5, 1,    3;    % 文化 vs ...1/5,1/7, 1/3,  1];   % 通勤 vs ...

在每个指标下的比较方案（构建判断矩阵）

%% 2. 构建方案层判断矩阵（针对每个准则）
% 方案顺序：A公司, B公司, C公司% 2.1 在“薪水”准则下，比较方案
Salary_Matrix = [1,   5,    3;    % A公司 vs [A, B, C]1/5, 1,    1/3;  % B公司 vs ...1/3, 3,    1];   % C公司 vs ...% 2.2 在“前景”准则下，比较方案
Potential_Matrix = [1,   1/5, 1/3;5,   1,   3;3,   1/3, 1];% 2.3 在“文化”准则下，比较方案
Culture_Matrix = [1,   1/3, 1/5;3,   1,   1/3;5,   3,   1];% 2.4 在“通勤”准则下，比较方案
Commute_Matrix = [1,   3,   5;1/3, 1,   3;1/5, 1/3, 1];

一致性检验

因为需要检验多个矩阵，所以这里对一致性检验的代码进行封装。

如果CR<0.1，则可以认为判断矩阵的一致性可以接受，否则需要对判断矩阵进行修正。

优先修改数值较大的判断，每次只微调1-2个元素，调整成倍数关系。

一致性指标 CI = (λ_max - n) / (n - 1)。

1.通过eig函数计算comparisonMatrix的特征值和特征向量，[eigenVectors, eigenValues] = eig(comparisonMatrix);eigenVectors是特征向量(列向量)构造的矩阵，eigenValues是特征值的对角矩阵。

eig - 特征值和特征向量 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/eig.html?searchHighlight=eig&s_tid=srchtitle_support_results_1_eig2.通过max(max(eigenValues))找到最大特征值，因为eigenValues是一个对角矩阵，max(eigenValues)求的是每列的最大值，得到的是一个行向量，max(max(eigenValues))返回这个行向量的最大值。

max - 数组的最大元素 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/double.max.html?searchHighlight=max&s_tid=srchtitle_support_results_1_max3.通过size(comparisonMatrix, 1)返回第一个维度的长度(行数)，这里两两进行的比较，所以行数和列数是相等的。

size - 数组大小 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/double.size.html?searchHighlight=size&s_tid=srchtitle_support_results_1_size3.求CI = (λ_max - n) / (n - 1)，RI是随机一致性指标，通过大量随机矩阵实验得出的经验值，可以在网上搜到。

4.一致性比例 CR = CI / RI，和0.1进行比较。

function [weights, CR] = ahp_eigenvalue_method(comparisonMatrix)% 计算特征值和特征向量[eigenVectors, eigenValues] = eig(comparisonMatrix);% 找到最大特征值maxEigenValue = max(max(eigenValues));% 一致性检验n = size(comparisonMatrix, 1);CI = (maxEigenValue - n) / (n - 1);RI_Table = [0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];RI = RI_Table(n);CR = CI / RI;
endfunction checkCR(criterionName, CR)if CR >= 0.1fprintf('【注意】"%s"准则下的判断矩阵一致性较差(CR = %.4f)，请重新评估！\n', criterionName, CR);elsefprintf('"%s"准则下方案得分计算成功，CR = %.4f < 0.1，通过检验。\n', criterionName, CR);end
end

层次单排序

采用特征值法和算术平均法两种相加求平均值的算法。

function [combinedWeights, CR, eigWeights, avgWeights] = ahp_calculate_combined(comparisonMatrix)% 方法1: 特征值法计算权重[eigWeights, CR] = ahp_eigenvalue_method(comparisonMatrix);% 方法2: 算术平均法计算权重avgWeights = ahp_arithmetic_mean_method(comparisonMatrix);% 综合方法：两种方法的平均值combinedWeights = (eigWeights + avgWeights) / 2;% 归一化确保总和为1combinedWeights = combinedWeights / sum(combinedWeights);
end

特征值法

如果一个判断矩阵是完全一致的，那么它的最大特征值对应的特征向量就是各元素的权重向量。

1.find(eigenValues == maxEigenValue, 1)查找第一个eigenValues == maxEigenValue的位置，也就是最大特征值所在的位置，[~,col]只要列数(因为特征向量是列向量)。

find - 查找非零元素的索引和值 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/find.html?searchHighlight=find&s_tid=srchtitle_support_results_1_find2.eigenVector = eigenVectors(:, col);得到col列。

3.weights = eigenVector / sum(eigenVector)将特征向量归一化得到权重（特征向量本身只是表示相对比例关系，数字的大小没有明确的物理意义，通过归一化后才能表示改因素的占比）。

function [weights, CR] = ahp_eigenvalue_method(comparisonMatrix)% 计算特征值和特征向量[eigenVectors, eigenValues] = eig(comparisonMatrix);% 找到最大特征值maxEigenValue = max(max(eigenValues));% 找到最大特征值对应的特征向量[~, col] = find(eigenValues == maxEigenValue, 1);eigenVector = eigenVectors(:, col);% 将特征向量归一化得到权重weights = eigenVector / sum(eigenVector);weights = weights'; % 转换为行向量
end

算术平均法

如果判断是一致的，那么每列元素的比例关系应该反映各元素的相对重要性。

1.[n, ~] = size(comparisonMatrix)获取矩阵的行数，通过normalizedMatrix = zeros(n, n)预留一个n*n大小的空间。

zeros - 创建全零数组 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/zeros.html?searchHighlight=zeros&s_tid=srchtitle_support_results_1_zeros2.columnSum = sum(comparisonMatrix(:, j))求得j列的和，normalizedMatrix(:, j) = comparisonMatrix(:, j) / columnSum，实现按列归一化（不同列之间的基准不一样，直接计算会导致结果的失真）。

3.mean(normalizedMatrix, 2)按行通过算术平均值得到权重。

mean - 数组的均值 - MATLABhttps://ww2.mathworks.cn/help/matlab/ref/double.mean.html?searchHighlight=mean&s_tid=srchtitle_support_results_1_mean4.将最终结果再进行一次归一化。

function weights = ahp_arithmetic_mean_method(comparisonMatrix)% 1. 按列归一化判断矩阵[n, ~] = size(comparisonMatrix);normalizedMatrix = zeros(n, n);for j = 1:ncolumnSum = sum(comparisonMatrix(:, j));normalizedMatrix(:, j) = comparisonMatrix(:, j) / columnSum;end% 2. 按行求算术平均值得到权重weights = mean(normalizedMatrix, 2)';% 3. 归一化确保总和为1weights = weights / sum(weights);
end

层次总排序

使用相同的方法计算出得分矩阵和准则权重向量（也可以通过Excel表格实现）。

% 计算准则层权重
[criteriaWeights, CR_criteria, eigWeights, avgWeights] = ahp_calculate_combined(CriteriaMatrix);
% 将每个准则下的方案得分组合成矩阵（每一行代表一个公司在不同准则下的得分）
optionScores = [salaryScores; potentialScores; cultureScores; commuteScores]';% 总得分 = 方案得分矩阵 × 准则权重向量
% optionScores: 3×4 矩阵 (3公司 × 4准则)
% criteriaWeights: 4×1 列向量 (4准则权重)
totalScores = optionScores * criteriaWeights';

MATLAB代码

% 层次分析法（AHP）示例：选择最佳工作offer（综合特征值法和算术平均法）
clear; clc;%% 1. 构建准则层判断矩阵并计算权重
% 准则顺序：1薪水, 2前景, 3文化, 4通勤
CriteriaMatrix = [1,  1/3, 3,    5;    % 薪水 vs [薪水,前景,文化,通勤]3,  1,   5,    7;    % 前景 vs ...1/3,1/5, 1,    3;    % 文化 vs ...1/5,1/7, 1/3,  1];   % 通勤 vs ...% 计算准则层权重并进行一致性检验（使用综合方法）
[criteriaWeights, CR_criteria, eigWeights, avgWeights] = ahp_calculate_combined(CriteriaMatrix);
if CR_criteria >= 0.1error('准则层判断矩阵一致性检验未通过(CR = %.4f)，请调整判断!', CR_criteria);
endfprintf('准则层权重计算成功！\n');
fprintf('特征值法权重: [%.4f, %.4f, %.4f, %.4f]\n', eigWeights);
fprintf('算术平均法权重: [%.4f, %.4f, %.4f, %.4f]\n', avgWeights);
fprintf('综合最终权重: [%.4f, %.4f, %.4f, %.4f]\n', criteriaWeights);
fprintf('准则层一致性比率 CR = %.4f < 0.1，通过检验。\n\n', CR_criteria);%% 2. 构建方案层判断矩阵（针对每个准则）
% 方案顺序：A公司, B公司, C公司% 2.1 在"薪水"准则下，比较方案
Salary_Matrix = [1,   5,    3;    % A公司 vs [A, B, C]1/5, 1,    1/3;  % B公司 vs ...1/3, 3,    1];   % C公司 vs ...
[salaryScores, CR_salary, ~, ~] = ahp_calculate_combined(Salary_Matrix);
checkCR('薪水', CR_salary);% 2.2 在"前景"准则下，比较方案
Potential_Matrix = [1,   1/5, 1/3;5,   1,   3;3,   1/3, 1];
[potentialScores, CR_potential, ~, ~] = ahp_calculate_combined(Potential_Matrix);
checkCR('前景', CR_potential);% 2.3 在"文化"准则下，比较方案
Culture_Matrix = [1,   1/3, 1/5;3,   1,   1/3;5,   3,   1];
[cultureScores, CR_culture, ~, ~] = ahp_calculate_combined(Culture_Matrix);
checkCR('文化', CR_culture);% 2.4 在"通勤"准则下，比较方案
Commute_Matrix = [1,   3,   5;1/3, 1,   3;1/5, 1/3, 1];
[commuteScores, CR_commute, ~, ~] = ahp_calculate_combined(Commute_Matrix);
checkCR('通勤', CR_commute);%% 3. 组合所有权重，计算方案总得分
% 将每个准则下的方案得分组合成矩阵（每一行代表一个公司在不同准则下的得分）
optionScores = [salaryScores; potentialScores; cultureScores; commuteScores]';fprintf('\n各公司在各准则下的得分：\n');
fprintf('      薪水     前景     文化     通勤\n');
companies = {'A公司', 'B公司', 'C公司'};
for i = 1:3fprintf('%s: ', companies{i});fprintf('%.4f  ', optionScores(i, :));fprintf('\n');
end% 总得分 = 方案得分矩阵 × 准则权重向量
% optionScores: 3×4 矩阵 (3公司 × 4准则)
% criteriaWeights: 4×1 列向量 (4准则权重)
totalScores = optionScores * criteriaWeights';%% 4. 显示最终结果
fprintf('\n===== 最终决策结果 =====\n');
for i = 1:length(totalScores)fprintf('%s 的综合得分: %.4f\n', companies{i}, totalScores(i));
end[bestScore, bestIndex] = max(totalScores);
fprintf('\n-> 最佳选择是: %s (得分: %.4f)\n', companies{bestIndex}, bestScore);%% --------------------- 新的综合权重计算函数 ---------------------
function [combinedWeights, CR, eigWeights, avgWeights] = ahp_calculate_combined(comparisonMatrix)% 方法1: 特征值法计算权重[eigWeights, CR] = ahp_eigenvalue_method(comparisonMatrix);% 方法2: 算术平均法计算权重avgWeights = ahp_arithmetic_mean_method(comparisonMatrix);% 综合方法：两种方法的平均值combinedWeights = (eigWeights + avgWeights) / 2;% 归一化确保总和为1combinedWeights = combinedWeights / sum(combinedWeights);
end%% --------------------- 特征值法函数 ---------------------
function [weights, CR] = ahp_eigenvalue_method(comparisonMatrix)% 计算特征值和特征向量[eigenVectors, eigenValues] = eig(comparisonMatrix);% 找到最大特征值maxEigenValue = max(max(eigenValues));% 找到最大特征值对应的特征向量[~, col] = find(eigenValues == maxEigenValue, 1);eigenVector = eigenVectors(:, col);% 将特征向量归一化得到权重weights = eigenVector / sum(eigenVector);weights = weights'; % 转换为行向量% 一致性检验n = size(comparisonMatrix, 1);CI = (maxEigenValue - n) / (n - 1);RI_Table = [0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];RI = RI_Table(n);CR = CI / RI;
end%% --------------------- 算术平均法函数 ---------------------
function weights = ahp_arithmetic_mean_method(comparisonMatrix)% 1. 按列归一化判断矩阵[n, ~] = size(comparisonMatrix);normalizedMatrix = zeros(n, n);for j = 1:ncolumnSum = sum(comparisonMatrix(:, j));normalizedMatrix(:, j) = comparisonMatrix(:, j) / columnSum;end% 2. 按行求算术平均值得到权重weights = mean(normalizedMatrix, 2)';% 3. 归一化确保总和为1weights = weights / sum(weights);
end%% --------------------- 一致性检查函数 ---------------------
function checkCR(criterionName, CR)if CR >= 0.1fprintf('【注意】"%s"准则下的判断矩阵一致性较差(CR = %.4f)，请重新评估！\n', criterionName, CR);elsefprintf('"%s"准则下方案得分计算成功，CR = %.4f < 0.1，通过检验。\n', criterionName, CR);end
end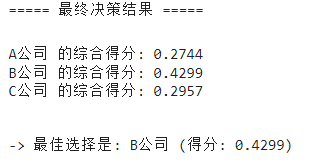

模糊综合评价

数学建模：评价决策类——模糊综合评价法-CSDN博客https://blog.csdn.net/qq_74301026/article/details/140857046?ops_request_misc=elastic_search_misc&request_id=779a489629af22787b93a134fc4e67a1&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-140857046-null-null.142^v102^pc_search_result_base3&utm_term=%E6%A8%A1%E7%B3%8A%E7%BB%BC%E5%90%88%E8%AF%84%E4%BB%B7&spm=1018.2226.3001.4187

熵权法

评价类——熵权法（Entropy Weight Method, EWM），完全客观评价-CSDN博客https://blog.csdn.net/qq_63913621/article/details/142306090?ops_request_misc=elastic_search_misc&request_id=8263af0353972ef2421b509a6a222a34&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-142306090-null-null.142^v102^pc_search_result_base3&utm_term=%E7%86%B5%E6%9D%83%E6%B3%95&spm=1018.2226.3001.4187

Topsis

评价类模型——TOPSIS（优劣解距离法） 清风建模笔记_topsis正向化处理方法哪个好-CSDN博客https://blog.csdn.net/q15623588795/article/details/137187820?ops_request_misc=elastic_search_misc&request_id=3a084b06c72f0e3d3cdd20c141adc447&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-137187820-null-null.142^v102^pc_search_result_base3&utm_term=Topsis&spm=1018.2226.3001.4187

灰色关联分析

【数学建模】灰色关联分析 + Matlab代码实现_灰色关联分析matlab代码-CSDN博客https://blog.csdn.net/weixin_51545953/article/details/111029419?ops_request_misc=elastic_search_misc&request_id=425c9626b1356f09f00c8c97571477a3&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-111029419-null-null.142^v102^pc_search_result_base3&utm_term=%E7%81%B0%E8%89%B2%E5%85%B3%E8%81%94%E5%88%86%E6%9E%90&spm=1018.2226.3001.4187

线性规划

数学建模：运筹优化类——线性规划-CSDN博客https://blog.csdn.net/qq_74301026/article/details/140833016?ops_request_misc=elastic_search_misc&request_id=b883ec5706feec92806a68f6642c8c9c&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-140833016-null-null.142^v102^pc_search_result_base3&utm_term=%E7%BA%BF%E6%80%A7%E8%A7%84%E5%88%92&spm=1018.2226.3001.4187

整数规划

从零开始学习数学建模：整数规划详解-CSDN博客https://blog.csdn.net/weidl001/article/details/143789160?ops_request_misc=elastic_search_misc&request_id=7e2035b1b8e997f23f7a6e65f6a5c7cb&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-143789160-null-null.142^v102^pc_search_result_base3&utm_term=%E6%95%B4%E6%95%B0%E8%A7%84%E5%88%92&spm=1018.2226.3001.4187

非线性规划

非线性规划详解：定义、求解方法与MATLAB实例-CSDN博客https://blog.csdn.net/qq_55433305/article/details/132874084?ops_request_misc=elastic_search_misc&request_id=de0fb80307cd88fb82c4eb1c73a88aef&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-132874084-null-null.142^v102^pc_search_result_base3&utm_term=%E9%9D%9E%E7%BA%BF%E6%80%A7%E8%A7%84%E5%88%92&spm=1018.2226.3001.4187

图论与最短路径算法

图论（二）：图的四种最短路径算法-CSDN博客https://blog.csdn.net/qibofang/article/details/51594673?ops_request_misc=elastic_search_misc&request_id=df7816629456ab1cd98f6c16896fdce6&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-51594673-null-null.142^v102^pc_search_result_base3&utm_term=%E5%9B%BE%E8%AE%BA%E4%B8%8E%E6%9C%80%E7%9F%AD%E8%B7%AF%E5%BE%84%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187

网络最大流问题

【运筹优化】网络最大流问题及三种求解算法详解 + Python代码实现_网络最大流问题例题详解-CSDN博客https://blog.csdn.net/weixin_51545953/article/details/129009589?ops_request_misc=elastic_search_misc&request_id=a432b7f6f2608cee7d95a5e3c322a43d&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-129009589-null-null.142^v102^pc_search_result_base3&utm_term=%E7%BD%91%E7%BB%9C%E6%9C%80%E5%A4%A7%E6%B5%81%E9%97%AE%E9%A2%98&spm=1018.2226.3001.4187

最小费用最大流问题

最小费用最大流问题与算法实现（Bellman-Ford、SPFA、Dijkstra）-CSDN博客https://blog.csdn.net/lym940928/article/details/90209172?ops_request_misc=elastic_search_misc&request_id=0a9b6e6b9fa4983ef308d817ba9cbc03&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-90209172-null-null.142^v102^pc_search_result_base3&utm_term=%E6%9C%80%E5%B0%8F%E8%B4%B9%E7%94%A8%E6%9C%80%E5%A4%A7%E6%B5%81%E9%97%AE%E9%A2%98&spm=1018.2226.3001.4187

旅行商问题

c++ 旅行商问题（动态规划）-CSDN博客https://blog.csdn.net/weixin_52115456/article/details/127799032?ops_request_misc=elastic_search_misc&request_id=dde1e14a620a90441c7fbec6f98cd744&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-127799032-null-null.142^v102^pc_search_result_base3&utm_term=%E6%97%85%E8%A1%8C%E5%95%86%E9%97%AE%E9%A2%98&spm=1018.2226.3001.4187

插值算法

图像插值技术解析-CSDN博客https://blog.csdn.net/syz201558503103/article/details/107192825?ops_request_misc=elastic_search_misc&request_id=6e9556a2cd542ed0af6788867ebf4cdb&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-107192825-null-null.142^v102^pc_search_result_base3&utm_term=%E6%8F%92%E5%80%BC%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187

拟合算法

【数学建模】——拟合算法-CSDN博客https://blog.csdn.net/weixin_73612682/article/details/131728372?ops_request_misc=elastic_search_misc&request_id=e28b24b3229075c2e779d4086ab6e98b&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-131728372-null-null.142^v102^pc_search_result_base3&utm_term=%E6%8B%9F%E5%90%88%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187

微分方程

高等数学（第四章：微分方程）-CSDN博客https://blog.csdn.net/weixin_49272453/article/details/143078443?ops_request_misc=elastic_search_misc&request_id=afa228a62a4969abe72b7855a60f26ec&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-143078443-null-null.142^v102^pc_search_result_base3&utm_term=%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B&spm=1018.2226.3001.4187

时间序列

15种时间序列预测方法总结(包含多种方法代码实现)-CSDN博客https://blog.csdn.net/java1314777/article/details/133272874?ops_request_misc=elastic_search_misc&request_id=8031bdfd00d02f962bc98a5f5b4dbea1&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-133272874-null-null.142^v102^pc_search_result_base3&utm_term=%E6%97%B6%E9%97%B4%E5%BA%8F%E5%88%97&spm=1018.2226.3001.4187

聚类分析

聚类分析（超全超详细版）-CSDN博客https://blog.csdn.net/demm868/article/details/127456264?ops_request_misc=elastic_search_misc&request_id=c371d493f6f382793c0d472a6e95968f&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-127456264-null-null.142^v102^pc_search_result_base3&utm_term=%E8%81%9A%E7%B1%BB%E5%88%86%E6%9E%90&spm=1018.2226.3001.4187

http://www.dtcms.com/a/348711.html

相关文章：

  • CUDA安装，pytorch库安装
  • 如何实现模版引擎
  • Shell 学习笔记 - Shell 三剑客篇
  • unity热更新总结
  • 【如何使用Redis实现分布式锁详解讲解】
  • [快乐数](哈希表)
  • 解决编译osgEarth中winsocket2.h找不到头文件问题
  • 基于Spark的热门旅游景点数据分析系统的设计-django+spider
  • Spring Boot测试陷阱：失败测试为何“传染”其他用例？
  • 【追涨抄底关注】副图指标 紫色主力线上行表明资金介入明显 配合价格突破时可靠性更高
  • deepseek连接solidworks设计一台非标设备 （part1）
  • 阿里云ECS服务器搭建ThinkPHP环境
  • 互联网大厂AI/大模型应用开发工程师面试剧本与解析
  • 阿里云云数据库RDS PostgreSQL管控功能使用
  • 基于SpringBoot的婚纱影楼服务预约平台【2026最新】
  • Spring AI 学习笔记(2)
  • GitHub 热榜项目 - 日榜(2025-08-24)
  • Wireshark USRP联合波形捕获（下）
  • windows上如何实现把指定网段的流量转发到指定的端口，有哪些界面化的软件用来配置完成，类似于 Linux中的iptables规则实现
  • 6.1Element UI布局容器
  • 【Luogu】P2602 [ZJOI2010] 数字计数 (数位DP)
  • 基于大模型的对话式推荐系统技术架构设计-- 大数据平台层
  • 07 - spring security基于数据库的账号密码
  • window11无法连接Fortinet SSL VPN
  • Elasticsearch如何确保数据一致性？
  • 『深度编码』操作系统-进程之间的通信方法
  • 记录一下TVT投稿过程
  • 阿里云大模型应用实战：从技术落地到业务提效
  • Dify 从入门到精通（第 53/100 篇）：Dify 的分布式架构（进阶篇）
  • 兑换汽水瓶