【数据结构入门】排序算法(2):直接选择排序->堆排序
目录
1.直接选择排序
1.1 思想
1.2 代码
2.堆排序
2.1 向下调整算法
2.1.1 代码
2.2 建堆
2.2.1 代码
2.3 正式排序
2.3.1 代码
3. 冒泡排序
3.1 思路
3.1.1 单趟排序
3.1.2 多趟排序
3.1.3优化
3.2 代码
1.直接选择排序
1.1 思想
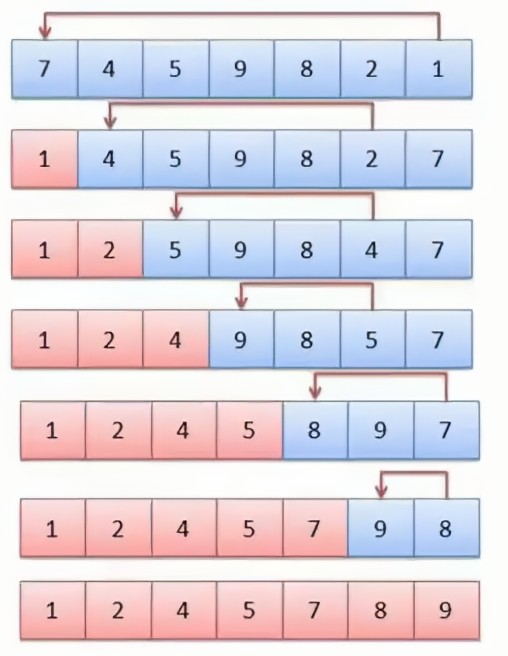
每次从未排序区中选择一个最小\最大的数字插入到排序区的最后一个位置。具体如下图所示:
优化:每一次遍历只选择一个最小的数,有些浪费,如果此时选择一个最小的数的同时也选一个最大的数,此时就能节省一半的时间。那么此时的思路如下:每次选择最小和最大的数放在最左边和最右边,每一次缩小左边界和右边界。
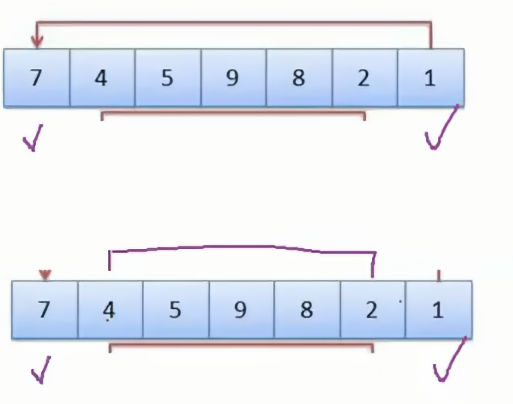
总体思路如下:
①维护两个下标begin和end作为边界。
②遍历[begin,end],设置mini即最小元素的下标、maxi即最大元素的下标为begin,若当前元素比mini所指的元素要小,那么就更新mini,同理更新maxi。
③循环之后将最大的元素与end元素进行交换,将最小的元素和begin进行交换。
④设置最新的begin和end,即更新为begin+1,end-1;
1.2 代码
错误代码演示:
void Swap(int* a,int* b)
{int tmp = *a;*a = *b;*b = tmp;
}// 直接选择排序
void selectSort(int* arr, int size)
{// 维护两个边界int begin = 0, end = size - 1;while (begin < end)// 等于的时候已经排序完毕{// 定义两个下标为最小元素和最大元素的下标int mini = begin;int maxi = begin;// 遍历闭区间内的所有数字,更新mini和maxifor (int i = begin + 1; i <= end; i++){if (arr[i] < arr[mini]){mini = i;// 此时更新mini}if (arr[i] > arr[maxi]){maxi = i;// 此时更新maxi}}// 循环结束之后,maxi是当前最大元素的下标,mini是当前最小元素的下标// 交换maxi元素和end元素。交换mini元素和begin元素Swap(&arr[mini],&arr[begin]);Swap(&arr[maxi],&arr[end]);// 更新左右边界--end;++begin;}
}错误的原因:如果遇到这种特殊情况,begin和min交换,max和end交换,此时相当于没有做出任何改变!第一步交换begin和min的时候是没有问题的,但是此时的maxi指向的并不是正确的位置,因为20已经被交换到最后一个位置了,此时需要重新计算maxi的位置。

由于begin和mini交换,此时的最大值已经在mini处了,所以此时更新maxi为mini。

正确代码如下:
void Swap(int* a,int* b)
{int tmp = *a;*a = *b;*b = tmp;
}// 直接选择排序
void selectSort(int* arr, int size)
{// 维护两个边界int begin = 0, end = size - 1;while (begin < end)// 等于的时候已经排序完毕{// 定义两个下标为最小元素和最大元素的下标int mini = begin;int maxi = begin;// 遍历闭区间内的所有数字,更新mini和maxifor (int i = begin + 1; i <= end; i++){if (arr[i] < arr[mini]){mini = i;// 此时更新mini}if (arr[i] > arr[maxi]){maxi = i;// 此时更新maxi}}// 循环结束之后,maxi是当前最大元素的下标,mini是当前最小元素的下标// 交换maxi元素和end元素。交换mini元素和begin元素Swap(&arr[mini],&arr[begin]);// 如果此时maxi和begin是重合的,那么需要重新找到maxiif (maxi == begin){maxi = mini; //此时mini和begin交换,max被换到了mini的位置上}Swap(&arr[maxi],&arr[end]);// 更新左右边界--end;++begin;}
}2.堆排序
堆排序的内容在之前堆的学习中已经学过了,这里简单再过一遍,如果还是有读者不懂,可以参照堆排序这篇文章。
2.1 向下调整算法
向下调整算法的前提是左右子树都是大堆或小堆;此时如果排的是升序,那么此时需要的是大堆,每次选择堆顶的数和最后一个数进行交换,再向下调整选择次大的数和倒数第二个数交换即可~
向下调整算法的逻辑:
①首先选择左孩子作为孩子中最大的节点,如果右孩子比左孩子大,那么就更新右孩子为最大的节点。
②如果当前节点的孩子节点没有越界,那么进入循环。首先判断右孩子是否越界并且右孩子如果比左孩子大,那么更新child节点为右孩子。
③在判断孩子节点和父亲节点哪一个大,如果孩子节点大那么就进行交换,如果父亲节点比孩子节点要大,说明本身就是大堆,那么就不需要进行调整了,此时直接退出循环即可。
2.1.1 代码
void adjustDown(int* arr, int n, int root)
{int parent = root;int child = 2 * parent + 1;// 默认左节点最大while (child < n)// 只要孩子节点不越界,那就继续循环{if (child + 1 < n && arr[child + 1] > arr[child]){// 说明右孩子更大,更新右孩子++child;}// 此时父亲节点和最大的孩子的节点进行判断if (arr[parent] < arr[child]){Swap(&arr[parent], &arr[child]);// 更新父亲节点,向下调整parent = child;child = child * 2 + 1;}else{// 此时满足大堆的条件,直接返回即可break;}}}2.2 建堆
每次从最后一个非叶子节点进行向下调整。
2.2.1 代码
// 堆排序 :数组、数组长度
void heapSort(int* arr,int n)
{// 建堆// 从最后一个非叶子结点开始向下调整for (int i = (n-1-1)/2; i >= 0; --i){adjustDown(arr,n,i);}
}2.3 正式排序
将堆建好之后,每次取大堆堆顶的数,交换到最后一个位置,再取出次大的数交换倒数第二个位置,以此类推;每次交换的时候需要向下调整,形成堆,才能取出最大的数。
2.3.1 代码
// 堆排序 :数组、数组长度
void heapSort(int* arr, int n)
{// 建堆// 从最后一个非叶子结点开始向下调整for (int i = (n - 1 - 1) / 2; i >= 0; --i){adjustDown(arr, n, i);}// 排序int end = n - 1;while (end > 0) // 1个数就不需要排序了 {Swap(arr[end], arr[0]); // 堆顶和最后一个元素交换// 继续调整成堆adjustDown(arr,end,0); // 将前n-1个数进行向下调整--end;}
}建堆的时间复杂度是O(n),堆排序的时间复杂度是n*Logn
3. 冒泡排序
3.1 思路
3.1.1 单趟排序
从第二个元素比较前一个元素,如果第二个元素小于第一个元素,就交换,循环一直到最后一个元素为止;
也就是说,每一次排序只会将最大的数字放到最后面,那么需要多少次排序呢?
3.1.2 多趟排序
我们只需要控制右边界就可以了,将右边界每次减少1个。
3.1.3优化
一趟排序结束后,没有交换元素,说明元素已经有序,那么就直接退出循环。
3.2 代码
// 冒泡排序void BubbleSort(int* arr, int size)
{int end = size;// 每一趟确定一个最大数while (end > 0){int flag = 1;// 单趟排序for (int i = 1; i < end; ++i){if (arr[i - 1] > arr[i]){Swap(&arr[i - 1], &arr[i]);flag = 0;}}if (flag == 1){break;// 提前退出循环}--end;}
}