Week 13: 深度学习补遗:RNN的训练
文章目录
- Week 13: 深度学习补遗:RNN的训练
- 摘要
- Abstract
- 1. RNN的训练
- 2. Backpropagation Through Time BPTT算法
- 3. RNN训练问题
- 总结
Week 13: 深度学习补遗:RNN的训练
摘要
本周主要跟随李宏毅老师的课程进度,继续学习了RNN的原理部分内容,对数学本质与底层逻辑方面知识继续进行深挖,对BPTT算法和梯度消失问题的解决方法进行了学习。
Abstract
This week, we mainly followed the course progress of Professor Hung-yi Lee and continued to study the principles of RNN. We continued to delve deeper into the mathematical essence and underlying logic, and learned about the BPTT algorithm and solutions to the gradient vanishing problem.
1. RNN的训练
以Slot Filling为例,对于当前的词汇xix^ixi,RNN输出向量yi^\hat{y^i}yi^,代表其属于某个Slot的可能性,即求yiy^iyi与yi^\hat{y^i}yi^的交叉熵损失函数。将多个词汇的损失求和即为网络的损失函数,需要注意的是,不可以打乱词汇的语序,因为RNN的前后文之间会相互影响,也就意味着xi+1x^{i+1}xi+1需要紧跟着xix^ixi输入。
RNN同样采用梯度下降法进行训练,但由于RNN工作在时间序列上,为了训练更加有效,采用了BPTT算法,考虑了时间维度的信息,在时间序列上更加有效。
2. Backpropagation Through Time BPTT算法
BPTT是反向传播算法为了在RNN上使用而改进的版本。
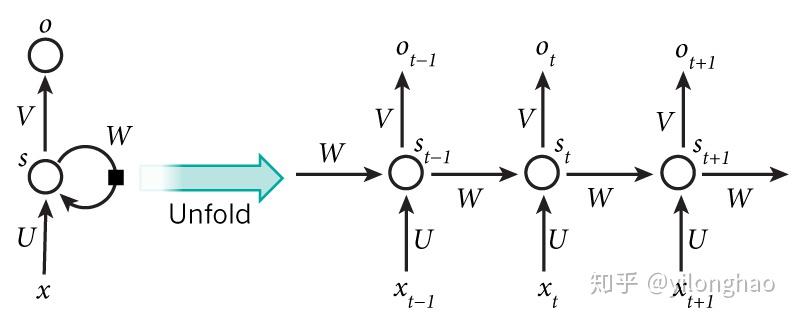
对于任意一个ttt时刻,有输出Ot=g(V⋅st+b2)O_t=g(V\cdot s_t+b_2)Ot=g(V⋅st+b2),而隐藏层st=f(U⋅xt+W⋅st−1+b1)s_t=f(U\cdot x_t+W\cdot s_{t-1}+b_1)st=f(U⋅xt+W⋅st−1+b1)。其中,st−1s_{t-1}st−1为上一时刻t−1t-1t−1的隐藏层存储,而xt−1x_{t-1}xt−1是当前词汇的输入,g(x)g(x)g(x)与f(x)f(x)f(x)是对应的激活函数。
而举例来说,如果f=tanhf=tanhf=tanh,g=softmaxg=softmaxg=softmax,损失函数定义为Cross Entrophy,即Lt=Et(yt,yt^)=−yt⋅logyt^L_t=E_t(y_t,\hat{y_t})=-y_t\cdot\log \hat{y_t}Lt=Et(yt,yt^)=−yt⋅logyt^。那么对于一个时间序列{(xt,yt),t=1,…,T}\{(x_t,y_t),t=1,\dots,T\}{(xt,yt),t=1,…,T},于是其整体损失函数就可以记为E=∑t=1TLt=−∑yt⋅logyt^E=\sum_{t=1}^T L_t=-\sum y_t\cdot\log\hat{y_t}E=∑t=1TLt=−∑yt⋅logyt^。
其和反向传播最大的不同,在于因为损失对各个权重的求导实际上等于对不同时刻误差对权重求导的总和。
∂L∂V=∑t∂Et∂V∂L∂W=∑t∂Et∂W∂L∂U=∑t∂Et∂U\frac{\partial L}{\partial V}=\sum_t \frac{\partial E_t}{\partial V} \\ \frac{\partial L}{\partial W}=\sum_t \frac{\partial E_t}{\partial W} \\ \frac{\partial L}{\partial U}=\sum_t \frac{\partial E_t}{\partial U} \\ ∂V∂L=t∑∂V∂Et∂W∂L=t∑∂W∂Et∂U∂L=t∑∂U∂Et
又因为st=f(U⋅xt+W⋅st−1+b1)s_t=f(U\cdot x_t+W\cdot s_{t-1}+b_1)st=f(U⋅xt+W⋅st−1+b1),因此在求导时后一步对前一步有依赖关系,因此需要进行链式求导,追溯到第一个时刻。
3. RNN训练问题
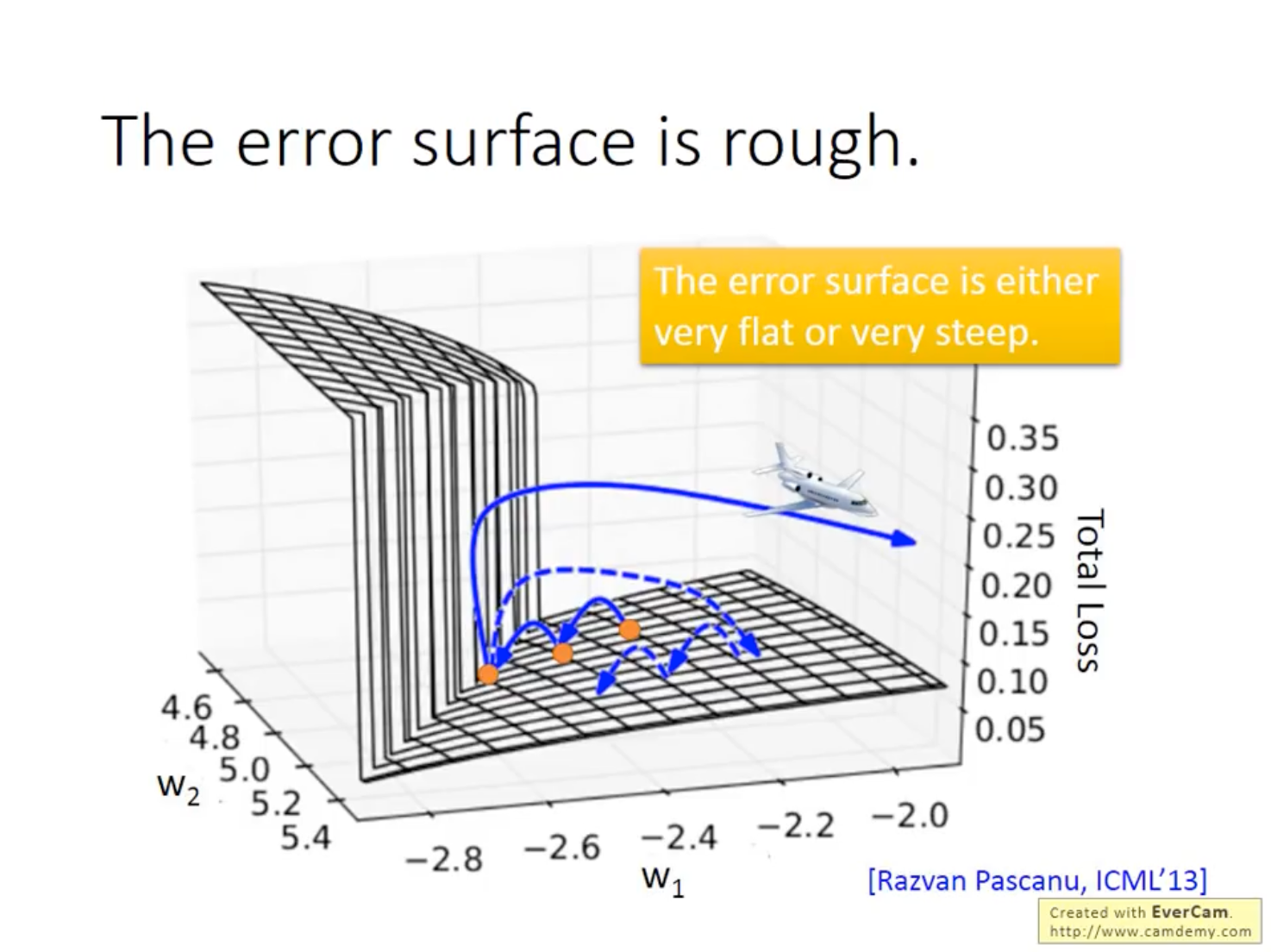
RNN的损失平面通常非常陡峭,导致训练时常常出现NaN或者0的情况,有一个trick非常奏效:Clipping,即设置一个阈值,在梯度大于阈值的时刻使用阈值代替梯度进行计算。
RNN还会出现很大块的梯度非常小的平面,即梯度消失的问题。前面常常提到的梯度消失问题主要来源于激活函数,即认为是Sigmoid函数导致的梯度消失,实际上在RNN上并不是这个原因,而将激活函数换成ReLU在RNN上的性能表现也一般会比较差。
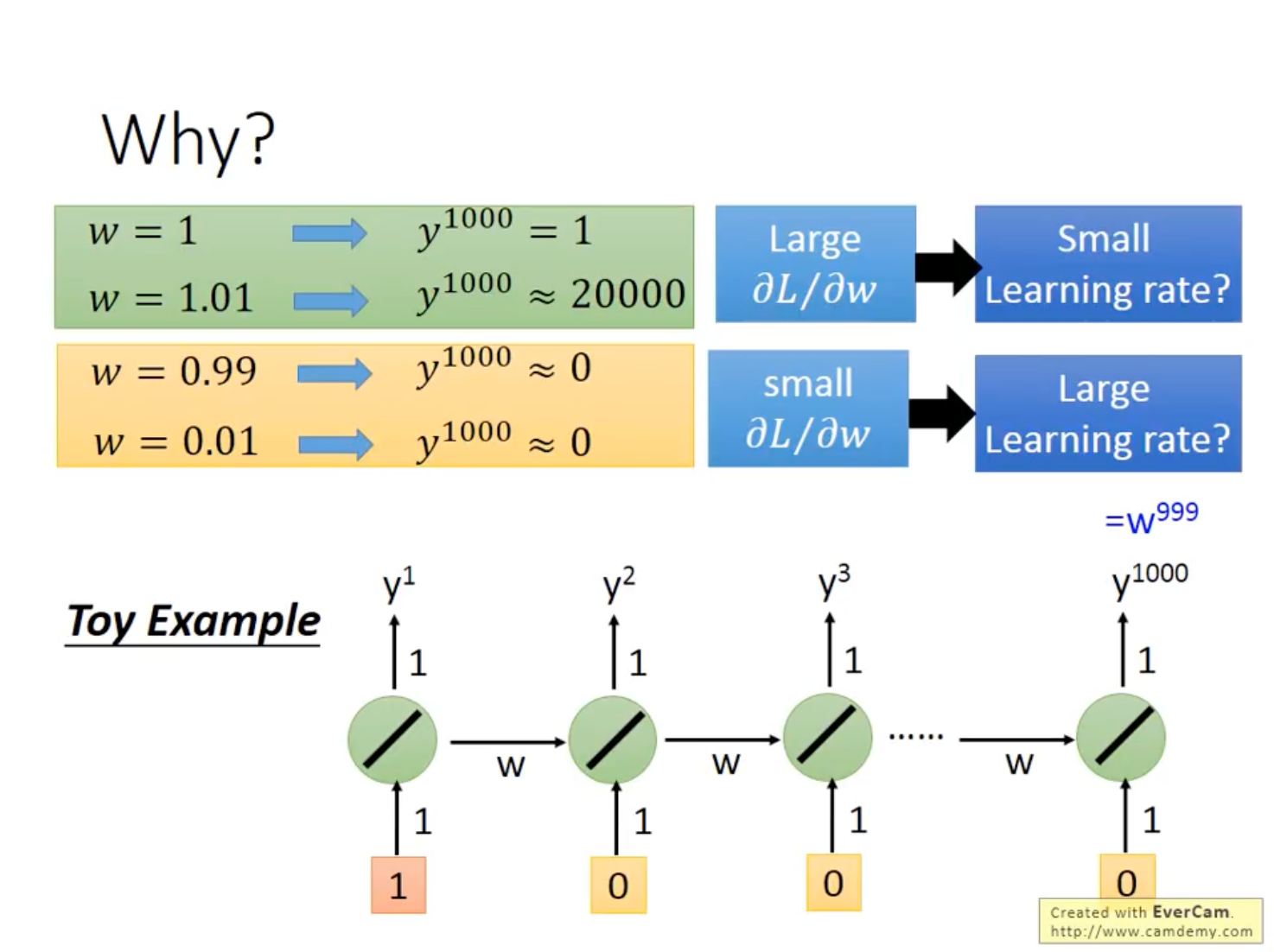
在前述的BPTT中,可知后面时刻隐藏层的值会受到前述所有时刻的影响,假设一个非常简单的RNN,隐藏层激活函数为线性,而每一层的存储层权重都为www,则最后一个时刻的隐藏层权重为w999w^{999}w999。易知当w=1.01w=1.01w=1.01时,w1000≈20000w^{1000}\approx 20000w1000≈20000;而当w=0.99w=0.99w=0.99时,w1000≈0w^{1000}\approx0w1000≈0。这就好比蝴蝶效应,权重的微小变化会给最后的梯度造成巨大影响。
而一个常用的用于解决梯度消失问题的方案就是使用LSTM(并非解决梯度爆炸),原因之一就是Memory的处理是加性的,不会累积权重,而除了遗忘门被打开,前时刻的影响同样不会消失。
还有一个方案是GRU,即Gated Recurrent Unit,门限循环单元。对比LSTM的三个门限,GRU只有两个门限,对比来说更加鲁棒。因此,在LSTM过拟合比较严重的情况下,可以尝试一下GRU。
在众多的解决方案中,还有一个更加有意思的解决方案。前文提到,RNN使用ReLU的激活函数性能不佳。但有趣的是,如果用单位矩阵初始化代替随机初始化时,RNN的性能会非常好,甚至超过LSTM。
总结
本周对RNN的BPTT算法进行了学习,了解了在时序模型上反向传播算法的实际运作流程,同时对RNN的梯度消失问题的出现原因,以及Clipping解决方案和单位矩阵初始化结局方案进行了一定的了解,同时对LSTM和GRU的模型优化解决方案也进行了认识。
