【数据结构】跳表的概率模型详解与其 C 代码实现
文章目录
- 介绍
- 关键组成部分
- 读者可以比对这张图片去理解跳表 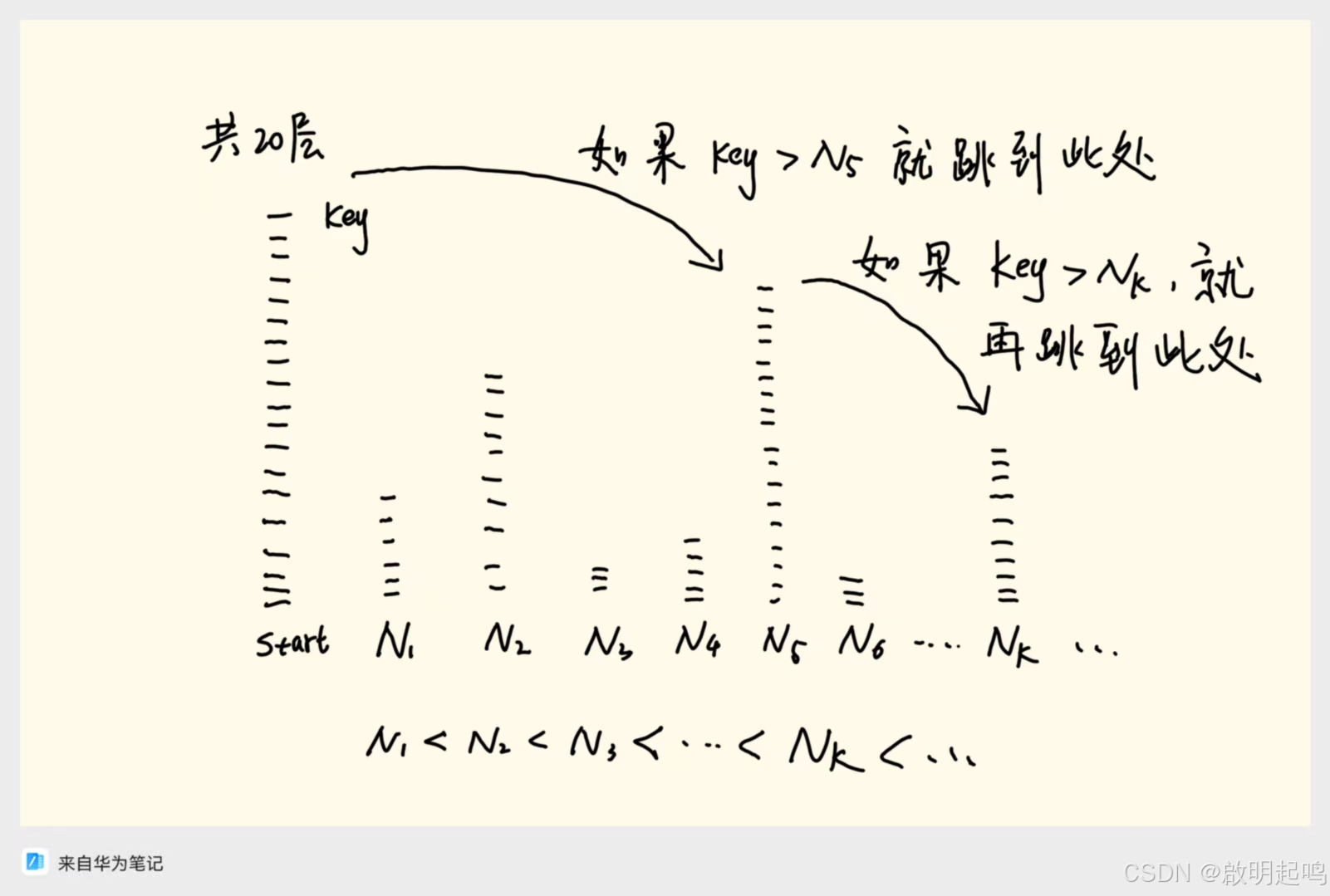 核心操作原理
- 算法的概率模型
- 跳表的 C代码实现
- 初始化跳跃表的节点、跳跃表本身
- 跳表插入节点
- 查找元素
- 更新元素值
- 删除跳表的某个节点
- 跳表的范围查询
- 销毁跳跃表
- 按层级打印跳跃表
- 测试代码(主函数)
推荐一个零声教育学习教程,个人觉得老师讲得不错,分享给大家:[Linux,Nginx,ZeroMQ,MySQL,Redis,fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,TCP/IP,协程,DPDK等技术内容,点击立即学习: https://github.com/0voice 链接。
介绍
跳表本质上是一种概率性的、有序的链表数据结构。它的核心目标是在有序链表的基础上,通过添加多层索引来加速查找、插入和删除操作,使得这些操作的平均时间复杂度能达到 O(log n),媲美平衡二叉搜索树(如AVL树、红黑树),但通常实现起来更简单,并且在某些并发场景下表现更好。
-
数据库与存储系统
LevelDB/RocksDB
应用:内存表(MemTable)实现
优势:高效的范围查询支持(SSTable构建);简单的并发控制;自然的键排序 -
数据库与存储系统
Apache Cassandra
应用:内存中的有序数据结构
优势:支持快速范围扫描和点查询 -
缓存系统
Redis有序集合(Sorted Set)
应用:有序集合的底层实现之一
优势:
1、O(log N) 的ZADD、ZRANGE、ZREM操作
2、高效的范围查询(ZRANGEBYSCORE)
3、与哈希表结合提供O(1)的点查询 -
搜索引擎与倒排索引
Lucene/Elasticsearch
应用:词典存储和区间查询
优势:快速术语查找;支持范围查询(如日期范围);高效的内存使用 -
网络路由与协议
分布式哈希表(DHT)
应用:Chord协议等P2P网络
优势:高效的关键字查找(O(log N)跳);自然支持区间查询 -
实时数据处理
1、时间序列数据库
应用:存储时间戳数据点
优势:高效的时间范围查询;按时间顺序插入;支持滚动窗口统计
2、金融交易系统
应用:订单簿管理
优势:快速价格查询;高效的范围扫描(获取买卖盘)
相比于各种树(红黑树、B/B+树、SPLAY 树),跳表的好处是很多的。
| 场景 | 跳表优势 | 平衡树劣势 |
|---|---|---|
| 并发环境 | 简单的细粒度锁或无锁实现 | 复杂的全局重平衡 |
| 范围查询 | 底层链表自然支持顺序访问 | 需要复杂的中序遍历 |
| 实现复杂度 | 代码简单,调试容易 | 旋转操作复杂,易出错 |
| 内存局部性 | 节点独立,缓存友好 | 指针密集,缓存不友好 |
| 性能预测 | 平均O(log N),实践稳定 | 最坏情况保证但常数因子大 |
你可以把它想象成在一个有序的单链表(第0层)上,建立了一层或多层的“快速通道”(高层索引)。高层索引跨越更多的低层节点,让你能更快地定位到目标区域。
跳表就像并排随机生长的小草,我们查找数据就是类似于玩马里奥游戏,从最左边某处跳下,先跳到离自己最近的长得最高的那棵草上,然后平级跳跃,直至不能再跳才下降一层找其他地方跳。

再仔细想一想,他真的很像一群并排生长的小草,小草的植高是随机的。

关键组成部分
-
节点:
存储实际的数据值(Key)。
包含一个forward指针数组(或叫next数组)。这个数组的大小等于该节点所在的层数(Level)。
forward[i] 指向该节点在第 i 层上的下一个节点。 -
层:
第0层: 最底层,包含所有元素,是一个完整的有序链表。
第1层及以上: 索引层。每一层都是其下一层的子集(一个更稀疏的有序链表)。层级越高,包含的节点越少,跨度越大。 -
头节点: 有一个特殊的头节点(Head),它的层数等于跳表当前的最大层数(MaxLevel)。头节点的 forward[i] 指向第 i 层的第一个实际节点(如果存在)。实际上是个一个哨兵节点。
-
最大层数: 一个预先设定的或动态调整的限制,防止层数无限增长。通常用 MaxLevel 表示。
-
随机层数: 这是跳表“概率性”的核心。当插入一个新节点时,不是固定地把它加到所有层,而是用类似抛硬币的方式(随机算法)决定它应该出现在哪些层。常见方法是:
- 从第1层开始(第0层肯定包含)。
- 生成一个随机数(比如0或1)。
- 如果结果是“正面”(例如1),则将该节点添加到当前层,并尝试向上一层(层数+1),重复抛硬币。
- 如果结果是“反面”(例如0),则停止增加层数。
- 确保节点至少在第0层(所以通常从第1层开始“抛硬币”)。
最终节点的层数 lvl 是一个介于1和MaxLevel之间的随机值(以1为起点)。这个节点将出现在第0层到第 lvl-1 层(或第1层到第 lvl 层,取决于定义)。
读者可以比对这张图片去理解跳表

核心操作原理
-
查找:
- 从最高层开始: 从头节点的最高层开始。
- 向右遍历: 沿着当前层的 forward 指针向右移动,直到下一个节点的值大于等于目标值。
- 向下一层: 如果下一个节点的值大于目标值,或者当前层没有下一个节点了,则下降到下一层。
- 重复: 重复步骤2和3,直到下降到第0层。
- 检查: 在第0层,当前节点的下一个节点如果等于目标值,则找到;否则不存在。
-
插入:
- 查找插入位置: 执行与查找类似的过程,但在下降过程中记录每一层可能需要更新的前驱节点(即在新节点插入后,其 forward 指针需要指向新节点的那些节点)。这些节点存储在 update 数组中,update[i] 保存第 i 层最后一个小于新节点值的节点。
-
生成随机层数: 使用抛硬币法决定新节点的层数 lvl。
-
创建新节点: 创建一个层数为 lvl 的新节点。
-
更新指针:(可选)更新最大层数: 如果 lvl 大于当前跳表的最大层数,则更新头节点的层数和跳表的 MaxLevel。
- 对于每一层 i (从0 到 lvl-1):
新节点的 forward[i] = update[i].forward[i]
update[i].forward[i] = 新节点
- 对于每一层 i (从0 到 lvl-1):
-
删除:
- 查找目标节点: 执行与查找类似的过程,同样记录每一层可能需要更新的前驱节点(存储在 update 数组中),这些节点的 forward 指针指向目标节点(或即将指向)。
- 找到目标节点: 在第0层,update[0].forward[0] 应该就是目标节点(如果存在)。
-
更新指针:
对于每一层 i (从0 到 目标节点层数-1):
如果 update[i].forward[i] 等于目标节点,则 update[i].forward[i] = 目标节点.forward[i] -
删除节点: 释放目标节点内存。
(可选)降低最大层数: 如果删除的是最高层的唯一节点,可能需要降低头节点的层数和跳表的 MaxLevel。
读者可以继续参考这张图

算法的概率模型
每个节点的层高有一套统计学操作程序决策,插入一个节点后,采用随机数判断是否提高层数。只要随机数都指向要上升一级,那就层数加 1;但是只要某一次没有指向层数上升的决定,那么决策终止,节点的层高就此敲定。
如果本科学过概率论,就会发现这就是经典的几何分布。
几何分布(Geometric Distribution)
- 定义:在一次伯努利试验中,成功的概率为 p(0 < p ≤ 1),失败的概率为 q = 1 – p。
独立重复地进行该试验,直到第一次成功为止,所进行的试验总次数记为随机变量 X。
则 X 服从参数为 p 的几何分布,记作 X∼Ge(p)X \sim Ge(p)X∼Ge(p) - 分布律(概率质量函数,PMF)
对于 k = 1, 2, 3, … P(X=k)=qk−1pP(X = k) = q^{k-1} pP(X=k)=qk−1p
解释:前 k – 1 次均失败(概率 q^{k-1}),第 k 次首次成功(概率 p)。 - 期望(均值)
E[X] = 1 / p - 方差(误差)
Var(X) = q / p² = (1 – p) / p²
期望与方差的计算都是使用无穷级数里的幂级数函数项级数的技巧方法,读者可以参考 《数学分析》。
对于我的 C 代码实现,一般来说,每次决策都是有一半的概率提升层数,也有一半的概率不提升节点的层数,故而平均层数为两层,
E[X]=1/p=2,当p=0.25时.E[X] = 1 / p=2, 当 p= 0.25 时.E[X]=1/p=2,当p=0.25时.
算法的查找复杂度(跳表总体层高 依较大概率 小于某个数)
我们记 NmaxN_{max}Nmax 为节点总数为 NNN 时的总体层高(它是一个随机变量),记 K(N) 为随机变量 NmaxN_{max}Nmax 的某个概率上界。一个节点的层高大于 K(N) 的概率是 1−12K(N)1-\frac{1}{2^{K(N)}}1−2K(N)1,故而
P(Nmax≤K(N))≤(1−12K(N))NP(N_{max} \leq K(N)) \leq (1-\frac{1}{2^{K(N)}})^NP(Nmax≤K(N))≤(1−2K(N)1)N
此时我们发现,如果 K(N)=2∗log2NK(N) =2*\log_2 NK(N)=2∗log2N
P(Nmax≤K(N))≤(1−1N2)N=(1e)N→0,当N→∞.P(N_{max} \leq K(N)) \leq (1-\frac{1}{N^2})^N=(\frac{1}{e})^N\to 0,\; 当\;N\to \infty.P(Nmax≤K(N))≤(1−N21)N=(e1)N→0,当N→∞.
所以我们可以算出跳跃表的层高是依概率小于 2log2N2\log_2 N2log2N 的。
跳表的 C代码实现
我们需要明确的一点是
数据结构=数据定义+数据的操作方法。数据结构 = 数据定义 + 数据的操作方法。 数据结构=数据定义+数据的操作方法。
首先是数据定义,每个节点都带有一个跳跃数组 forword,与键值对。跳表需要包括头节点(头节点是一个哨兵节点)、当前元素数量、当前层高。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <limits.h>// 跳表就像并排随机生长的小草,我们查找数据就是类似于玩马里奥游戏,从最左边某处跳下,先跳到离自己最近的长得最高的那棵草上,然后平级跳跃,直至不能再跳才下降一层找其他地方跳
// 跳表最大层数,越大说明稀疏程度越高
#define MAX_LEVEL 16// 跳表节点结构
typedef struct Node {int key;int value;struct Node **forward; // 每层的前进指针数组
} Node;// 跳表结构
typedef struct SkipList {Node *header; // 头节点int level; // 当前最大层数int size; // 元素数量
} SkipList;
初始化跳跃表的节点、跳跃表本身
// 创建新节点
Node* create_node(int level, int key, int value) {Node *node = (Node*)malloc(sizeof(Node));node->key = key;node->value = value;node->forward = (Node**)malloc(sizeof(Node*) * (level + 1));for (int i = 0; i <= level; i++) {node->forward[i] = NULL;}return node;
}// 初始化跳表
SkipList* create_skip_list() {SkipList *sl = (SkipList*)malloc(sizeof(SkipList));sl->level = 0;sl->size = 0;sl->header = create_node(MAX_LEVEL, INT_MIN, 0); // 头节点键值为最小值,头节点的层高一开始也是为 0// 初始化头节点的每层指针for (int i = 0; i <= MAX_LEVEL; i++) {sl->header->forward[i] = NULL;}srand(time(NULL)); // 初始化随机数种子return sl;
}跳表插入节点
我们可以使用奇数与偶数的均匀二分,从而实现成功/失败概率的 1:1。插入,首先进行的是跳跃查找定位到专门的节点。
// 随机生成节点层数(偶数与奇数对半分)
int random_level() {int level = 0;while (rand() % 2 == 0 && level < MAX_LEVEL) {level++;}return level;
}// 插入元素
void insert(SkipList *sl, int key, int value) {Node *update[MAX_LEVEL + 1]; // 记录条,记录 key 的下确界Node *current = sl->header;// 从最高层开始查找插入位置for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}update[i] = current;}// 移动到第0层的下一个节点current = current->forward[0];// 如果键已存在,更新值if (current != NULL && current->key == key) {current->value = value;return;}// 随机生成新节点层数int new_level = random_level();// 如果新节点层数大于当前跳表层数,更新高层指针if (new_level > sl->level) {for (int i = sl->level + 1; i <= new_level; i++) {update[i] = sl->header;}sl->level = new_level;}// 创建新节点Node *new_node = create_node(new_level, key, value);// 更新指针for (int i = 0; i <= new_level; i++) {new_node->forward[i] = update[i]->forward[i];update[i]->forward[i] = new_node;}sl->size++;
}查找元素
// 查找元素
Node* search(SkipList *sl, int key) {Node *current = sl->header; // current 是下确界// 从最高层开始查找for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}}// 移动到第0层的下一个节点current = current->forward[0];if (current != NULL && current->key == key) {return current;}return NULL;
}更新元素值
// 更新元素值
void update(SkipList *sl, int key, int new_value) {Node *node = search(sl, key);if (node != NULL) {node->value = new_value;}
}
删除跳表的某个节点
// 删除元素
void delete(SkipList *sl, int key) {Node *update[MAX_LEVEL + 1]; // update 是下确界Node *current = sl->header;// 从最高层开始查找for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < key) {current = current->forward[i];}update[i] = current;}// 移动到第0层的下一个节点current = current->forward[0];// 如果节点存在则删除if (current != NULL && current->key == key) {// 更新各层指针for (int i = 0; i <= sl->level; i++) {if (update[i]->forward[i] != current) break;update[i]->forward[i] = current->forward[i];}// 释放节点内存free(current->forward);free(current);// 更新跳表层数while (sl->level > 0 && sl->header->forward[sl->level] == NULL) {sl->level--;}sl->size--;}
}跳表的范围查询
我们可以类比的是 B+ 树的范围查询,因为它和 B+ 树的范围查询一样好用。读者可以参考我写的关于 B+ 树的博客。
// 范围查询(高效实现)
void range_query(SkipList *sl, int start_key, int end_key) {Node *current = sl->header;// 定位到起始位置for (int i = sl->level; i >= 0; i--) {while (current->forward[i] != NULL && current->forward[i]->key < start_key) {current = current->forward[i];}}// 移动到起始节点current = current->forward[0];// 遍历范围内的节点printf("Range query [%d, %d]:\n", start_key, end_key);while (current != NULL && current->key <= end_key) {printf(" (%d, %d)\n", current->key, current->value);current = current->forward[0];}
}
销毁跳跃表
// 销毁跳表
void free_skip_list(SkipList *sl) {Node *current = sl->header;Node *next;// 释放所有节点,跳表往右收缩,先删头节点while (current != NULL) {next = current->forward[0];free(current->forward);free(current);current = next;}//free(sl->header);free(sl);printf("all component have been release\n");
}
按层级打印跳跃表
// 打印跳表结构(调试用)
void print_skip_list(SkipList *sl) {printf("Skip List (level=%d, size=%d):\n", sl->level, sl->size);for (int i = sl->level; i >= 0; i--) {Node *node = sl->header->forward[i];printf("Level %d: ", i);while (node != NULL) {printf("%d(%d) → ", node->key, node->value);node = node->forward[i];}printf("NULL\n");}
}
测试代码(主函数)
test_num 是指代测试规模。我们先插入一堆节点,然后按层级打印,紧接着是更改、查询操作,最后是范围查询、删除一个节点后再展示层级打印。
#define test_num 100
int main() {SkipList *sl = create_skip_list();for (int i=0; i<test_num; i++) {insert(sl, i+3, 3*i+17);}// 打印跳表结构print_skip_list(sl);// 查找示例Node *found = search(sl, 5);if (found) {printf("\nFound key 5, value=%d\n", found->value);}// 更新示例update(sl, 5, 555);printf("After update key 5: ");found = search(sl, 5);if (found) printf("value=%d\n", found->value);// 范围查询示例range_query(sl, test_num, 3*test_num);// 删除示例delete(sl, 5);printf("\nAfter deleting key 5:\n");print_skip_list(sl);// 销毁跳表free_skip_list(sl);return 0;
}
代码运行
qiming@qiming:~/share/CTASK/data-structure$ gcc -o skiplist skiplist.c
qiming@qiming:~/share/CTASK/data-structure$ ./skiplist
Skip List (level=7, size=100):
Level 7: 77(239) → NULL
Level 6: 77(239) → NULL
Level 5: 57(179) → 77(239) → NULL
Level 4: 30(98) → 57(179) → 68(212) → 77(239) → 88(272) → NULL
Level 3: 16(56) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 97(299) → NULL
Level 2: 5(23) → 14(50) → 16(56) → 18(62) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 90(278) → 94(290) → 96(296) → 97(299) → NULL
Level 1: 5(23) → 7(29) → 11(41) → 12(44) → 14(50) → 16(56) → 17(59) → 18(62) → 22(74) → 25(83) → 26(86) → 27(89) → 30(98) → 31(101) → 33(107) → 39(125) → 40(128) → 44(140) → 45(143) → 48(152) → 49(155) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 62(194) → 63(197) → 66(206) → 68(212) → 70(218) → 74(230) → 77(239) → 80(248) → 88(272) → 90(278) → 92(284) → 93(287) → 94(290) → 96(296) → 97(299) → NULL
Level 0: 3(17) → 4(20) → 5(23) → 6(26) → 7(29) → 8(32) → 9(35) → 10(38) → 11(41) → 12(44) → 13(47) → 14(50) → 15(53) → 16(56) → 17(59) → 18(62) → 19(65) → 20(68) → 21(71) → 22(74) → 23(77) → 24(80) → 25(83) → 26(86) → 27(89) → 28(92) → 29(95) → 30(98) → 31(101) → 32(104) → 33(107) → 34(110) → 35(113) → 36(116) → 37(119) → 38(122) → 39(125) → 40(128) → 41(131) → 42(134) → 43(137) → 44(140) → 45(143) → 46(146) → 47(149) → 48(152) → 49(155) → 50(158) → 51(161) → 52(164) → 53(167) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 59(185) → 60(188) → 61(191) → 62(194) → 63(197) → 64(200) → 65(203) → 66(206) → 67(209) → 68(212) → 69(215) → 70(218) → 71(221) → 72(224) → 73(227) → 74(230) → 75(233) → 76(236) → 77(239) → 78(242) → 79(245) → 80(248) → 81(251) → 82(254) → 83(257) → 84(260) → 85(263) → 86(266) → 87(269) → 88(272) → 89(275) → 90(278) → 91(281) → 92(284) → 93(287) → 94(290) → 95(293) → 96(296) → 97(299) → 98(302) → 99(305) → 100(308) → 101(311) → 102(314) → NULLFound key 5, value=23
After update key 5: value=555
Range query [100, 300]:(100, 308)(101, 311)(102, 314)After deleting key 5:
Skip List (level=7, size=99):
Level 7: 77(239) → NULL
Level 6: 77(239) → NULL
Level 5: 57(179) → 77(239) → NULL
Level 4: 30(98) → 57(179) → 68(212) → 77(239) → 88(272) → NULL
Level 3: 16(56) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 97(299) → NULL
Level 2: 14(50) → 16(56) → 18(62) → 30(98) → 39(125) → 57(179) → 58(182) → 62(194) → 66(206) → 68(212) → 77(239) → 80(248) → 88(272) → 90(278) → 94(290) → 96(296) → 97(299) → NULL
Level 1: 7(29) → 11(41) → 12(44) → 14(50) → 16(56) → 17(59) → 18(62) → 22(74) → 25(83) → 26(86) → 27(89) → 30(98) → 31(101) → 33(107) → 39(125) → 40(128) → 44(140) → 45(143) → 48(152) → 49(155) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 62(194) → 63(197) → 66(206) → 68(212) → 70(218) → 74(230) → 77(239) → 80(248) → 88(272) → 90(278) → 92(284) → 93(287) → 94(290) → 96(296) → 97(299) → NULL
Level 0: 3(17) → 4(20) → 6(26) → 7(29) → 8(32) → 9(35) → 10(38) → 11(41) → 12(44) → 13(47) → 14(50) → 15(53) → 16(56) → 17(59) → 18(62) → 19(65) → 20(68) → 21(71) → 22(74) → 23(77) → 24(80) → 25(83) → 26(86) → 27(89) → 28(92) → 29(95) → 30(98) → 31(101) → 32(104) → 33(107) → 34(110) → 35(113) → 36(116) → 37(119) → 38(122) → 39(125) → 40(128) → 41(131) → 42(134) → 43(137) → 44(140) → 45(143) → 46(146) → 47(149) → 48(152) → 49(155) → 50(158) → 51(161) → 52(164) → 53(167) → 54(170) → 55(173) → 56(176) → 57(179) → 58(182) → 59(185) → 60(188) → 61(191) → 62(194) → 63(197) → 64(200) → 65(203) → 66(206) → 67(209) → 68(212) → 69(215) → 70(218) → 71(221) → 72(224) → 73(227) → 74(230) → 75(233) → 76(236) → 77(239) → 78(242) → 79(245) → 80(248) → 81(251) → 82(254) → 83(257) → 84(260) → 85(263) → 86(266) → 87(269) → 88(272) → 89(275) → 90(278) → 91(281) → 92(284) → 93(287) → 94(290) → 95(293) → 96(296) → 97(299) → 98(302) → 99(305) → 100(308) → 101(311) → 102(314) → NULL
all component have been release
qiming@qiming:~/share/CTASK/data-structure$ 