线性回归：从原理到实战的完整指南

在机器学习的世界里，线性回归就像是入门者的 "Hello World"，它简单却蕴含着机器学习的核心思想。无论是预测房价、股票走势，还是分析用户行为，线性回归都以其直观性和高效性占据着重要地位。本文将带你从理论到实践，全面掌握线性回归的精髓。

一、线性回归的核心思想：找到最优拟合线

线性回归的本质是通过属性的线性组合来进行预测的模型。想象一下，当我们想通过房屋大小预测房价时，希望找到一条直线能最好地描述两者的关系 —— 这就是线性回归的核心目标：找到一条直线（或高维空间中的超平面），使得预测值与真实值之间的误差最小化。

线性模型的数学表达

对于单个属性的样本，线性模型可表示为

其中：

x 是输入特征（如房屋大小）

w 是权重参数（斜率）

b 是偏置参数（截距）

f(x) 是模型的预测值

当面对多个特征时，多元线性回归的一般形式为：

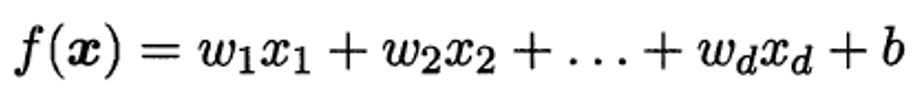
用向量形式可简洁表示为：

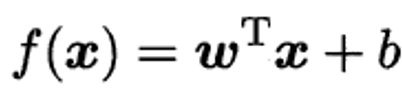
其中 w 是权重向量，x 是特征向量，wT 表示 w 的转置。

二、如何找到最优的拟合线？最小二乘法的魔力

有了模型形式，接下来需要解决的问题是：如何确定最优的参数 w 和 b？这里就要用到最小二乘法—— 一种基于均方误差最小化的模型求解方法。

最小二乘法的原理

最小二乘法的核心思想是：找到一条直线，使所有样本到直线上的欧氏距离之和最小。数学上，我们需要最小化的误差函数（损失函数）为：

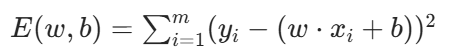
其中 m 是样本数量，yi​ 是真实值，w⋅xi​+b 是预测值。

参数求解过程

通过对误差函数 E(w,b) 分别求 w 和 b 的偏导数，并令导数为 0，可解得最优参数：

权重 w 的最优解：通过样本特征与均值的协方差计算

偏置 b 的最优解：b=yˉ​−w⋅xˉ（其中 yˉ​ 是真实值均值，xˉ 是特征均值）

这个过程被称为线性回归模型的参数估计，它通过数学推导直接得到解析解，无需迭代优化。

三、如何评估模型好坏？关键指标解析

训练出模型后，需要用评估指标来判断其拟合效果。线性回归常用的评估指标有以下几种：

1. 误差平方和（SSE/RSS）

误差平方和（Sum of Squared Errors 或 Residual Sum of Squares）计算所有样本预测值与真实值差值的平方和：

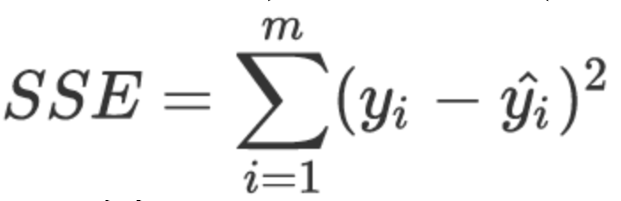
其中 y^​i​ 是模型对第 i 个样本的预测值。SSE 值越小，说明模型拟合效果越好。

2. 均方误差（MSE）

均方误差（Mean Square Error）是 SSE 的平均值，消除了样本数量对误差值的影响：

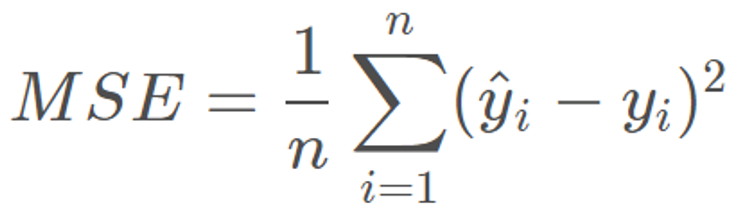
3. 决定系数（R²）

R² 是最常用的评估指标之一，它表示模型解释数据变异的能力

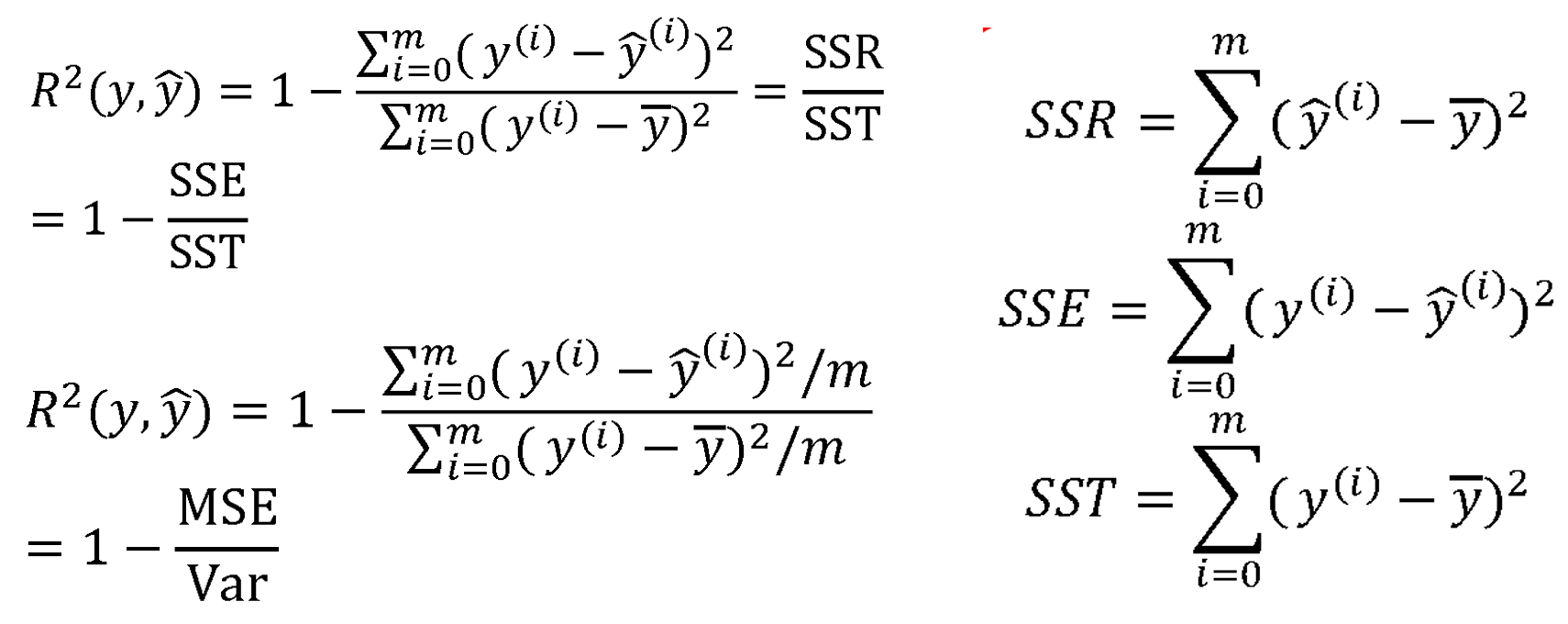
R² 取值范围为 (−∞,1]

越接近 1，表示模型拟合效果越好

当 R² = 1 时，模型完全拟合所有样本

当 R² ≤ 0 时，说明模型效果不如直接使用均值预测

四、实战：用 scikit-learn 实现线性回归预测

理论掌握后，让我们通过实战巩固。以下是使用 scikit-learn 库实现线性回归的示例代码：

核心 API 介绍

scikit-learn 中线性回归的核心类是 linear_model.LinearRegression，其主要参数包括：

fit_intercept	是否有截据，如果没有则直线过原点，默认为Ture。
normalize	是否将数据归一化,默认为False。

加州房价预测示例

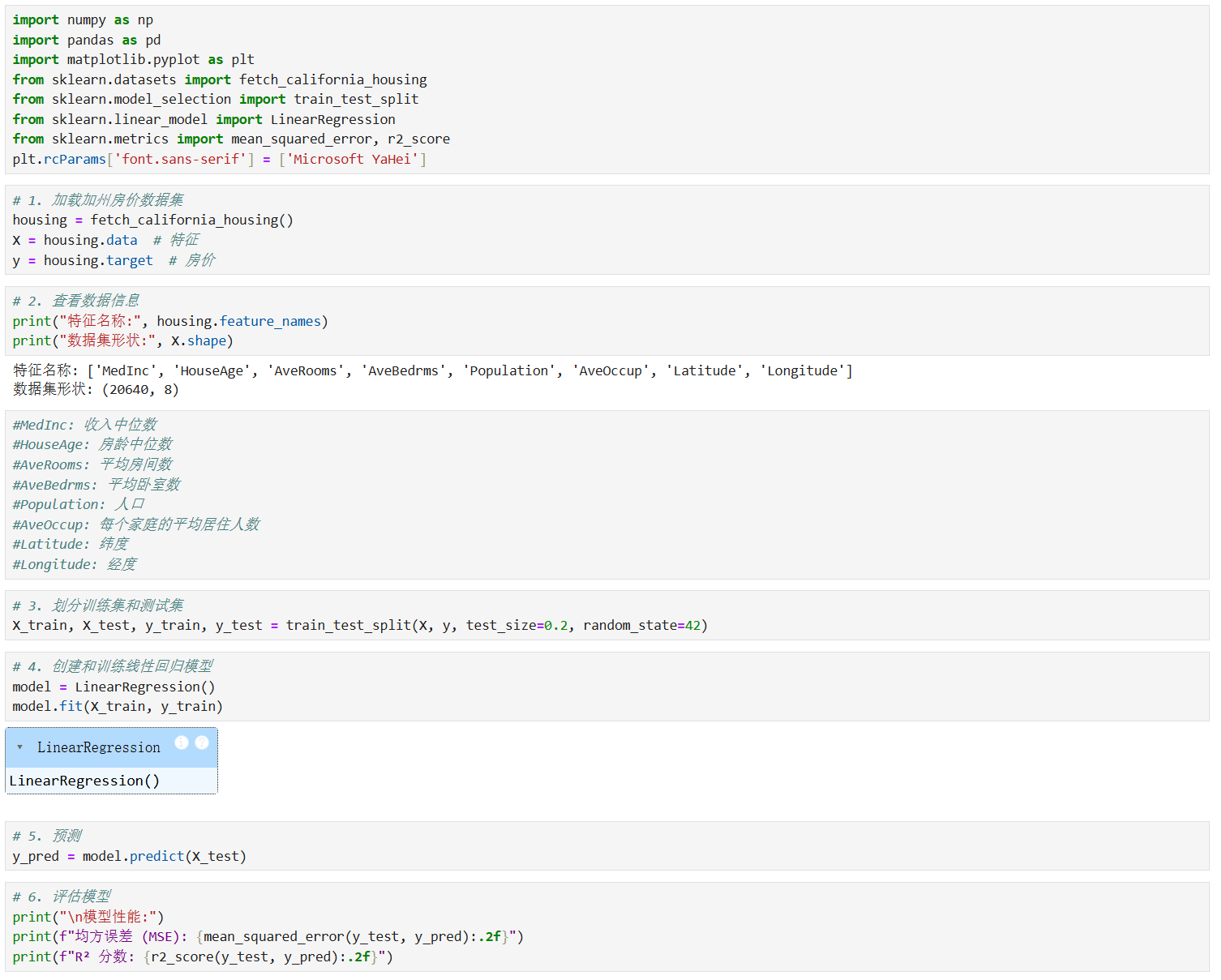
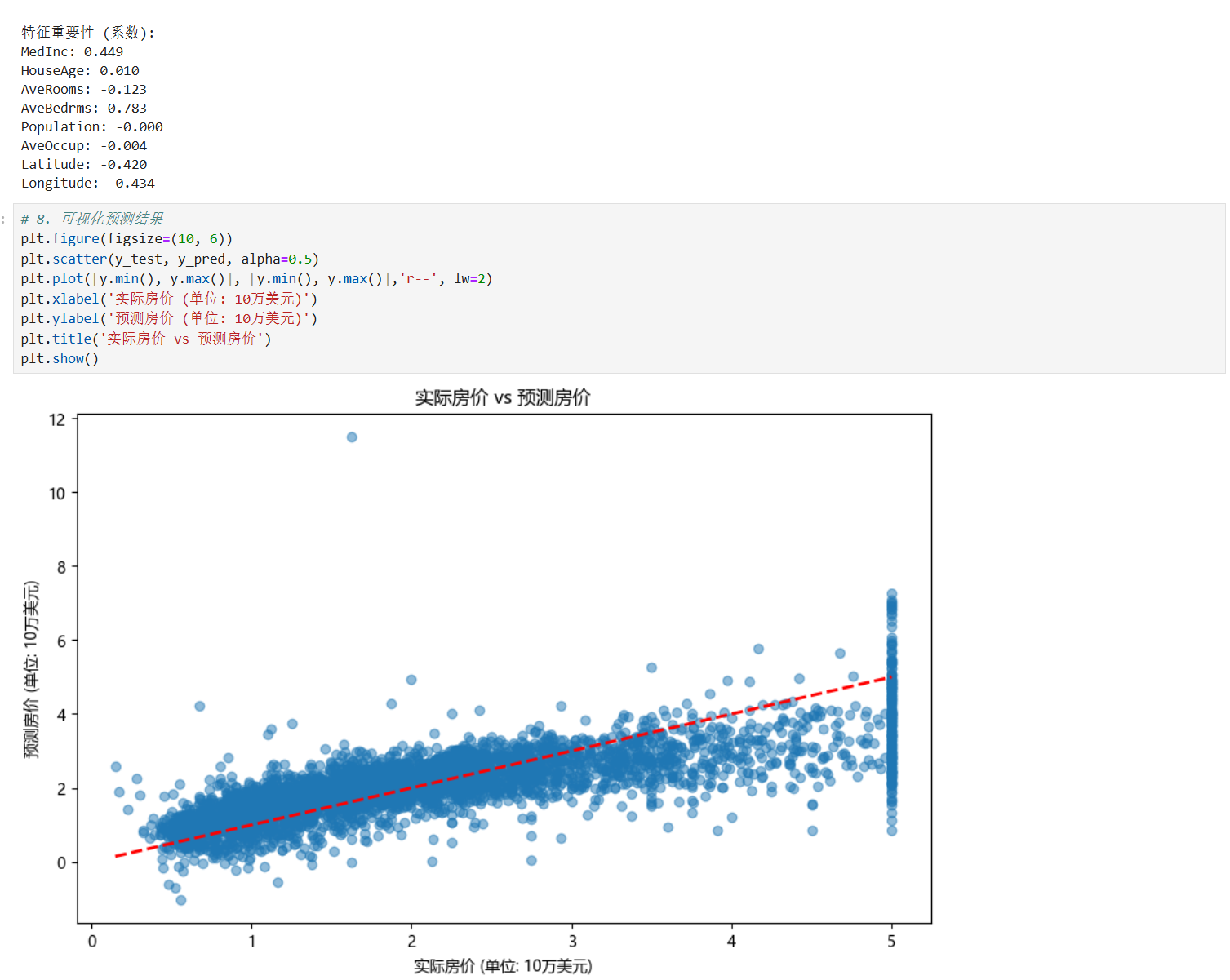
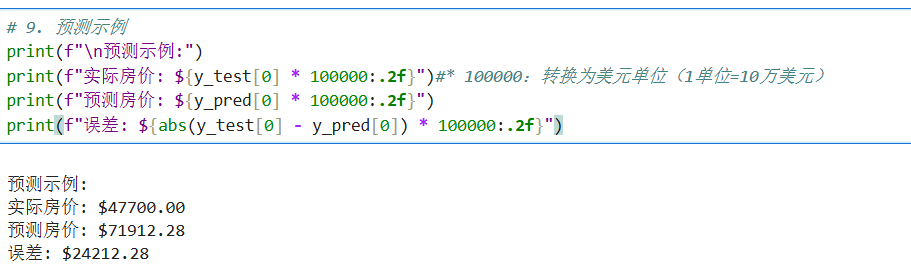
学生考试表现影响因素预测示例

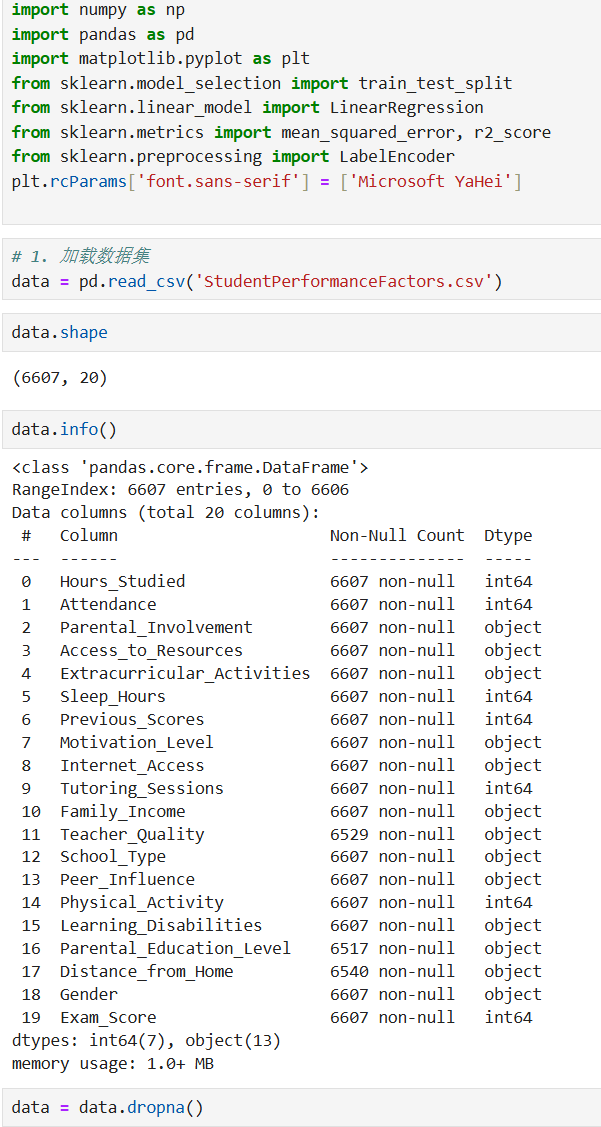
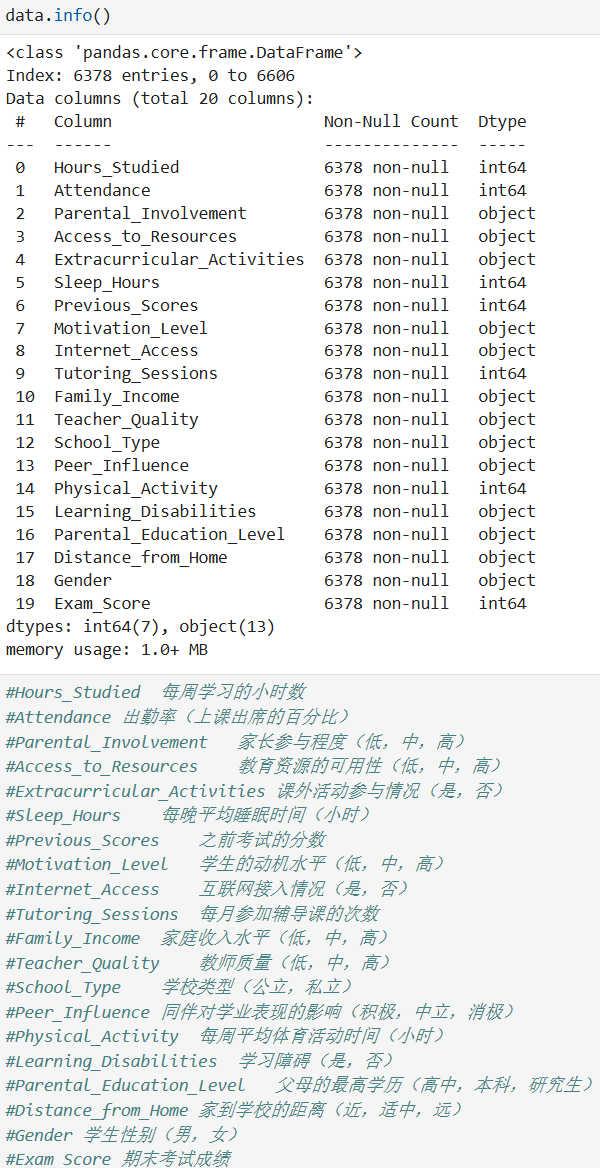
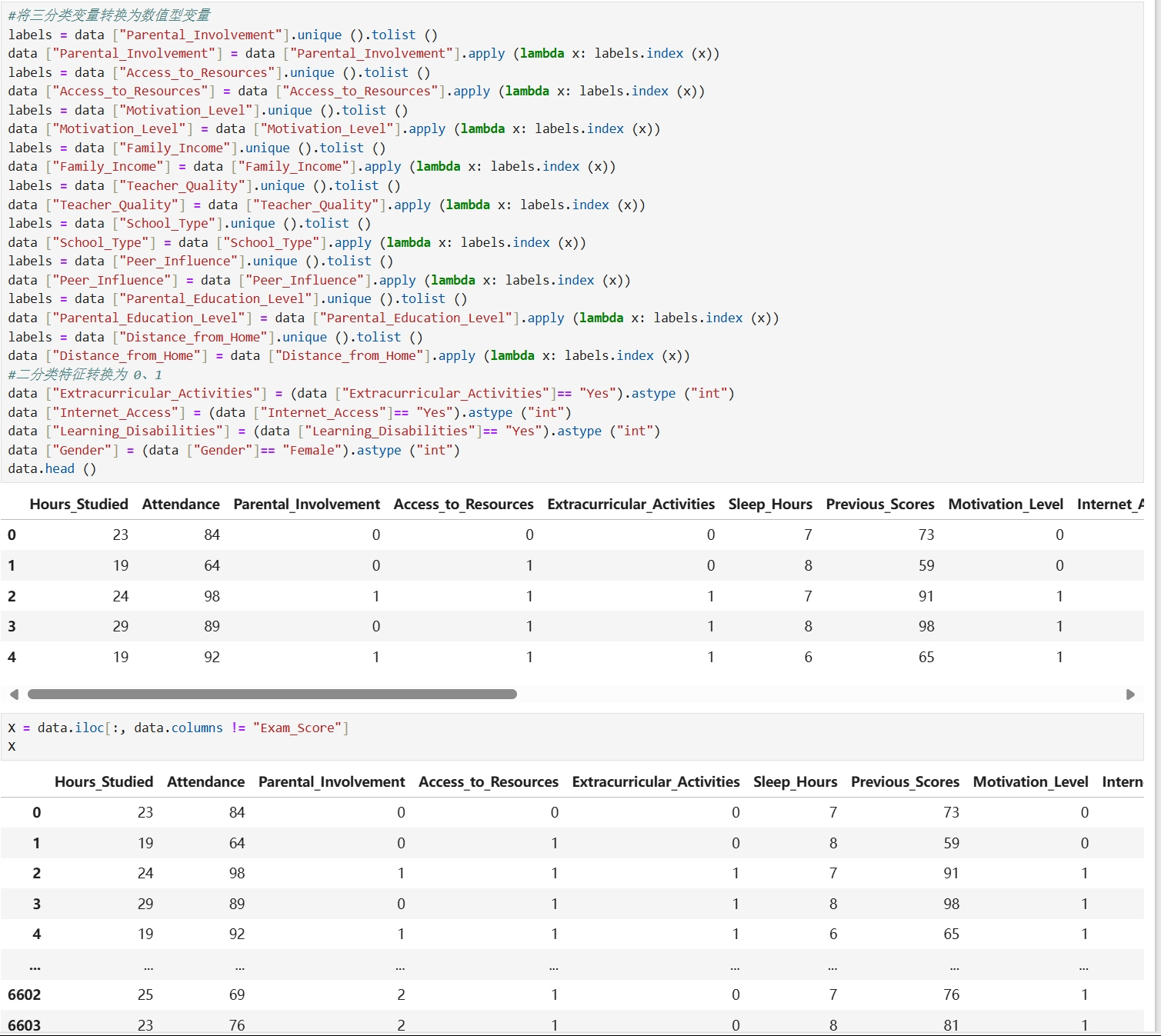
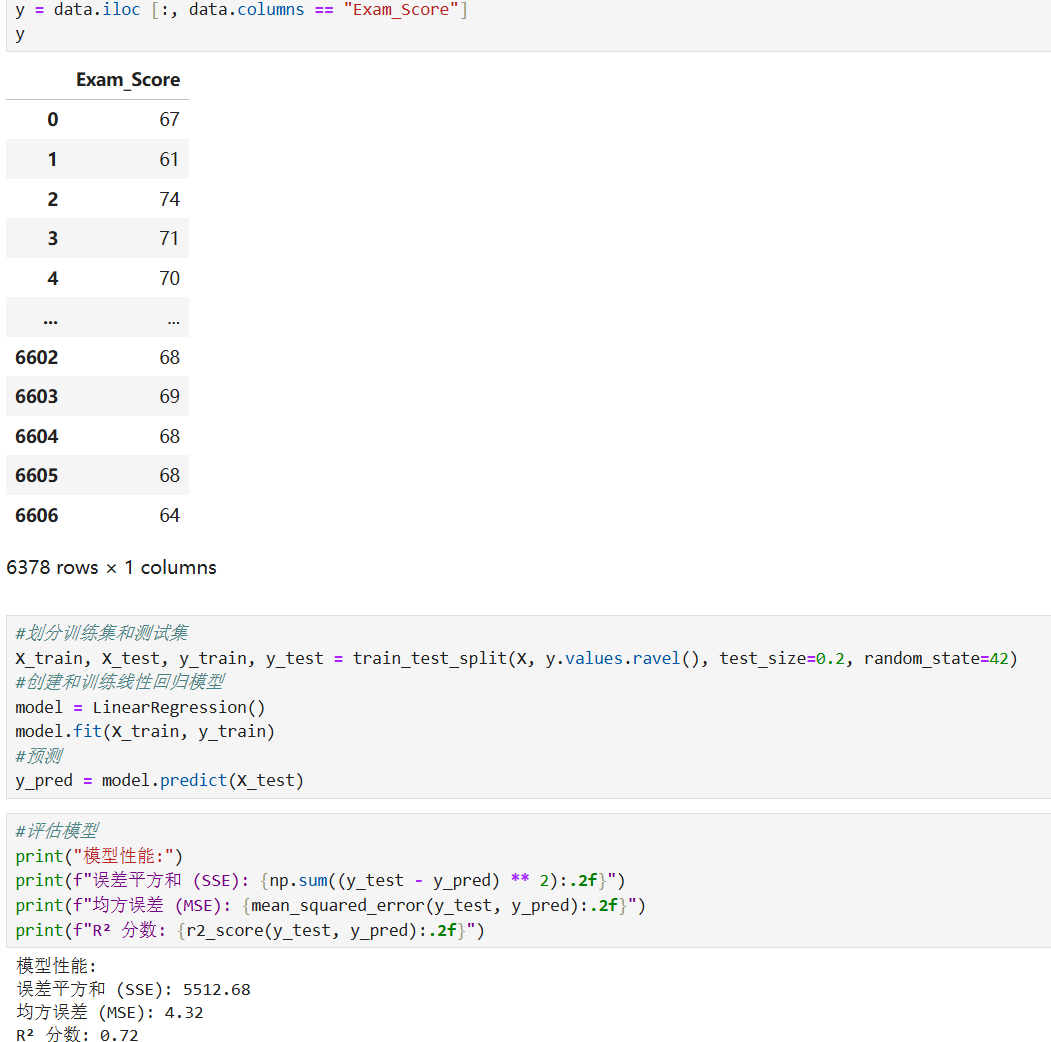
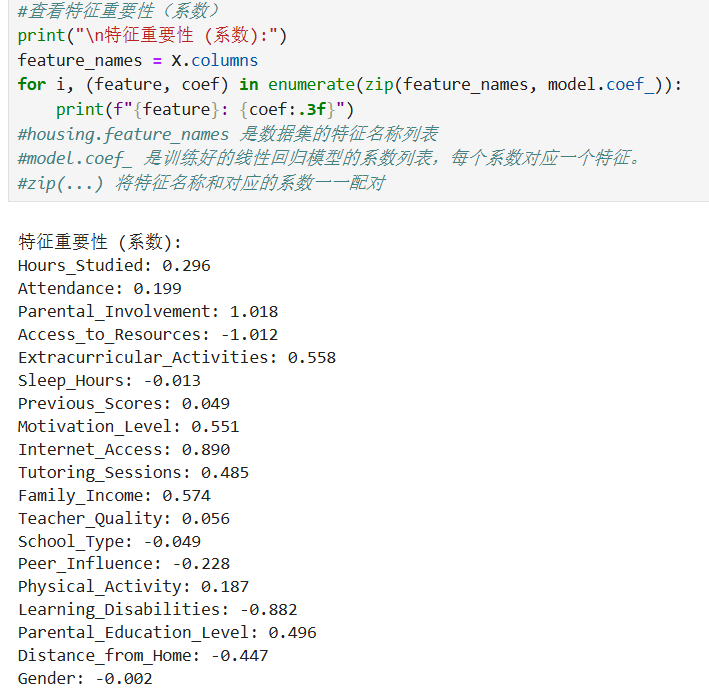
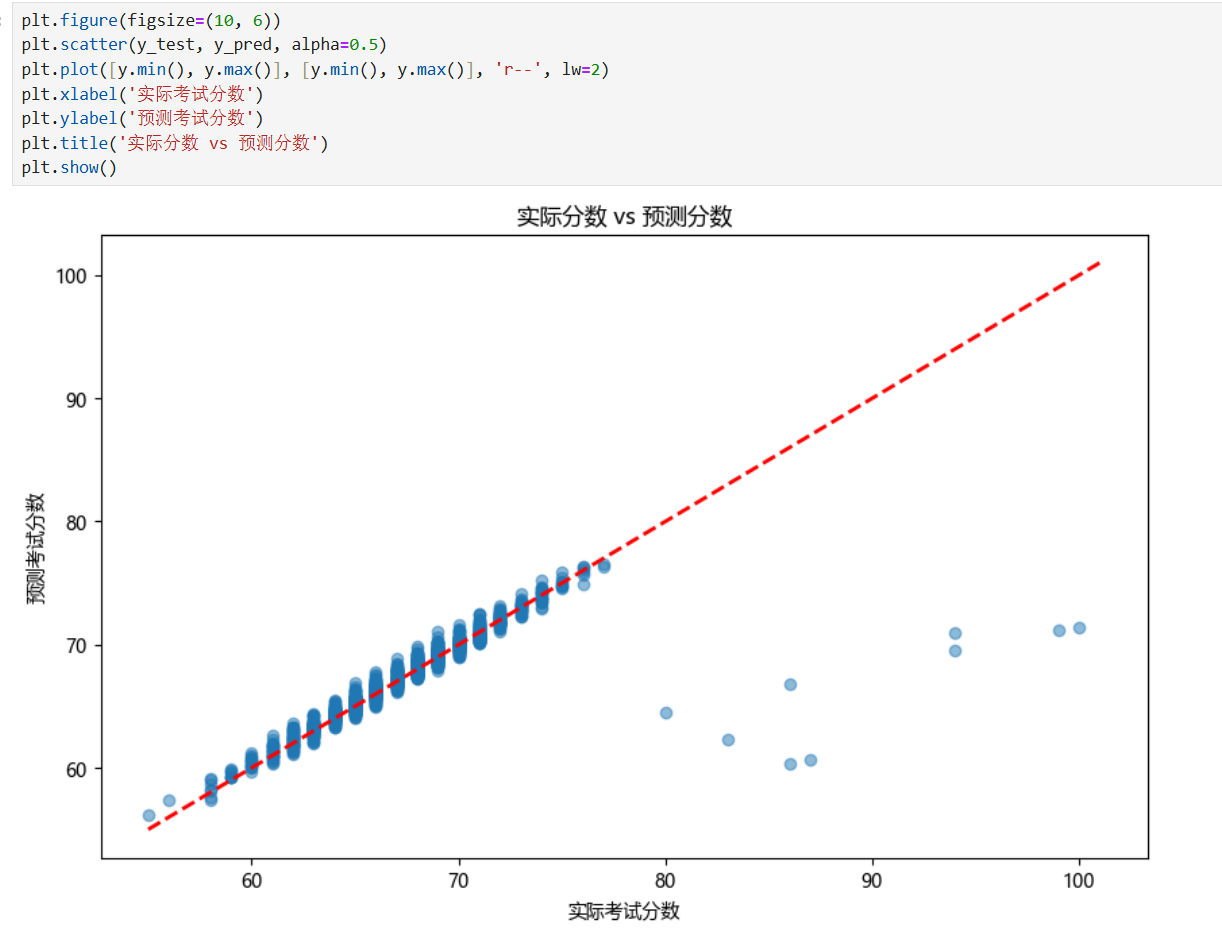
五、线性回归的局限性与扩展

尽管线性回归简单高效，但它也有局限性：

只能捕捉线性关系，无法处理特征与目标之间的非线性关系

对异常值敏感，异常值可能严重影响拟合线

默认假设特征之间相互独立，无法处理多重共线性问题

针对这些局限，可采用以下扩展方法：

多项式回归：通过添加多项式特征捕捉非线性关系

正则化方法（如 Ridge、Lasso）：解决过拟合和多重共线性问题

robust 回归：降低异常值对模型的影响

总结

线性回归作为最基础的机器学习模型，不仅是入门机器学习的绝佳起点，也是许多复杂模型的基石。相信通过本文，你已经掌握了线性回归的核心原理（最小二乘法）、评估指标（SSE、MSE、R²）和实战方法。