机器学习--线性回归
目录
一、线性回归:用数学公式 “画” 出规律
二、核心密码:怎么找到那条 “最好的线”?
三、怎么判断线 “画” 得好不好?
四、动手试了试:用线性回归预测房价
五、碎碎念:线性回归的 “能” 与 “不能”
六、代码与运行结果
用一条直线 “猜” 对世界?线性回归的入门笔记
今天啃完了机器学习里的 “线性回归”,感觉像解开了一个藏在数据里的密码 —— 原来那些看似杂乱的数字,真的能被一条直线 “驯服”。这篇笔记想聊聊我对线性回归的理解,还有自己动手用它预测房价的过程,尽量说得像聊天,毕竟我也是刚入门的新手~
一、线性回归:用数学公式 “画” 出规律
刚开始学的时候,我总觉得 “回归” 这两个字有点唬人,其实说白了特简单:它就是用一堆已知的特征(比如房子的面积、房龄),通过一个线性公式预测一个结果(比如房价)。
举个例子,假设我们想通过 “房屋大小” 预测 “价格”,线性回归会帮我们找到一个公式:
价格 = 权重 × 房屋大小 + 截距
换成数学符号就是 f(x) = wx + b 。这里的 w 是权重(可以理解为 “房屋大小对价格的影响程度”),b 是截距(当房屋大小为 0 时的基准价格)。如果特征不止一个呢?比如还要考虑房龄、地段,那就变成了 “多元线性回归”,公式扩展成 f(x) = w₁x₁ + w₂x₂ + ... + wₙxₙ + b ,本质还是特征的线性组合,只是从 “直线” 变成了高维空间的 “超平面”。
二、核心密码:怎么找到那条 “最好的线”?
光知道公式没用,关键是怎么确定 w 和 b 的值。今天学的 “最小二乘法”,堪称线性回归的 “灵魂算法”。
它的思路特别朴素:找一条线,让所有数据点到这条线的 “距离” 总和最小。这里的 “距离” 不是几何上的垂直距离,而是预测值和真实值的差的平方(专业点叫 “均方误差”)。为什么用平方?因为平方能放大偏差大的点,逼着算法更关注那些 “离群” 的数据。
用公式表示就是:我们要最小化 E(w,b) = Σ(y真实 - y预测)² ,其中 y预测 = wx + b 。通过对 w 和 b 求导并令导数为 0,就能算出最优的 w 和 b —— 这一步推导的时候感觉像在解高中数学题,没想到居然是机器学习的基础操作,还挺奇妙的。
三、怎么判断线 “画” 得好不好?
算出 w 和 b 之后,总得知道这条线靠谱不靠谱吧?今天学了两个核心指标:
1、均方误差(MSE):简单说就是 “平均误差的平方”,公式是 MSE = (1/n)Σ(y真实 - y预测)² 。数值越小,说明预测和真实值越接近。
2、R²(决定系数):这个指标更直观,它的范围在 0 到 1 之间。越接近 1,说明这条线能解释的数据规律越多,拟合效果越好。比如我后来用它预测房价时,R² 达到了 0.6,老师说对于入门案例已经算不错了~
四、动手试了试:用线性回归预测房价
今天的练习是用加州房价数据做预测,从 0 到 1 敲代码的过程还挺有成就感的,分享几个关键步骤:
1、拿到数据:用 fetch_california_housing 加载了数据集,里面有平均收入、房龄、纬度等 8 个特征,目标是预测房价(单位是万美元)。
2、拆数据:把数据分成训练集(80%)和测试集(20%),训练集用来找 w 和 b ,测试集用来检验效果 —— 就像先做题再考试。
3、归一化:用 StandardScaler 把特征缩放到同一尺度,老师说这样能让 w 的大小更能反映特征的重要性(比如 “平均收入” 的权重比 “纬度” 大,说明收入对房价影响更显著)。
4、建模预测:调用 LinearRegression 模型,拟合后得到了 8 个特征的权重和截距。有意思的是,“纬度” 的权重是负的,可能说明越往北房价越低?
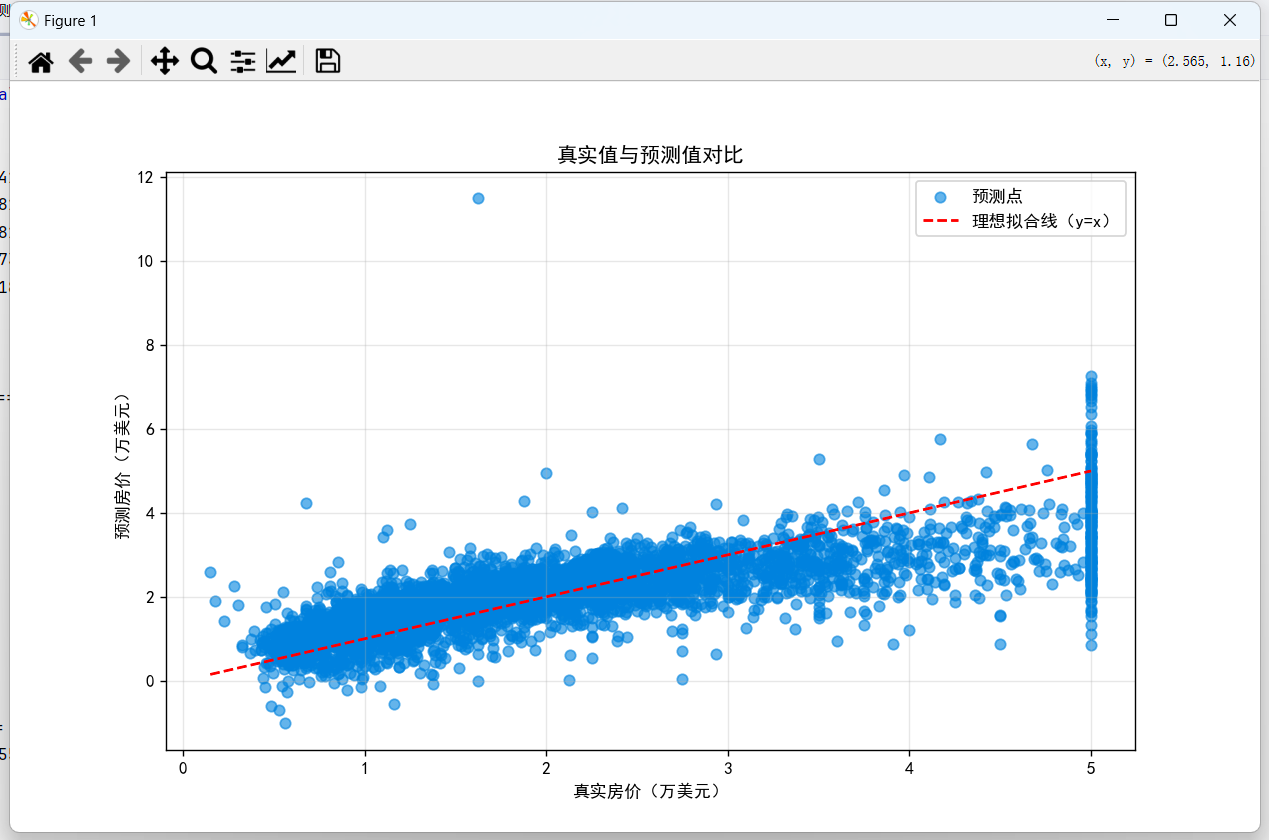
5、画张图看看:把测试集的真实房价和预测房价画成散点图,再画一条 y=x 的参考线 —— 如果点都靠近这条线,说明预测得准。我画出来的点虽然有点散,但整体趋势是对的,MSE 是 0.52,R² 是 0.6,也算没白费功夫~
五、碎碎念:线性回归的 “能” 与 “不能”
今天学完最大的感受是:线性回归简单,但不简单。
它的 “能”:逻辑清晰、计算快,还能直观看到每个特征的影响(比如哪个因素对房价影响大),特别适合入门理解 “机器学习怎么从数据中找规律”。
它的 “不能”:只能处理线性关系,如果数据分布是曲线(比如 “年龄和收入” 可能先增后减),用直线拟合就会差很多。不过没关系,这只是第一步嘛。
六、代码与运行结果
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt# 设置中文字体,解决中文显示问题
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示问题# 加载加州房价数据集
california = fetch_california_housing()
X = california.data # 特征数据
y = california.target # 目标值(房价,单位:万美元)# 转换为DataFrame便于查看
feature_names = ['平均收入', '房龄', '平均房间数', '平均卧室数', '人口数', '平均占用率', '纬度', '经度']
data = pd.DataFrame(X, columns=feature_names)
data['房价'] = y# 查看数据集基本信息
print("数据集前5行:")
print(data.head())
print("\n数据集形状:", data.shape)# 划分特征与目标变量
X = data[feature_names].values
y = data['房价'].values# 划分训练集和测试集(8:2)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 归一化处理
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 训练线性回归模型
model = LinearRegression(fit_intercept=True)
model.fit(X_train_scaled, y_train)# 预测与评估
y_pred = model.predict(X_test_scaled)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)# 输出模型结果
print("\n===== 线性回归模型参数 =====")
print(f"截距(b):{model.intercept_:.4f}")
print("特征权重(w):")
for fea, w in zip(feature_names, model.coef_):print(f" {fea}:{w:.4f}")print("\n===== 模型评估指标 =====")
print(f"测试集均方误差(MSE):{mse:.4f}")
print(f"测试集R²值:{r2:.4f}")# 查看前5个测试样本的预测结果
print("\n前5个样本的预测结果:")
for i in range(5):print(f"真实房价:{y_test[i]:.2f}万美元,预测房价:{y_pred[i]:.2f}万美元")plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred, alpha=0.6, label='预测点') # 散点图显示真实值与预测值关系
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', label='理想拟合线(y=x)') # 参考线
plt.xlabel('真实房价(万美元)') # 修正为房价相关标签
plt.ylabel('预测房价(万美元)')
plt.title('真实值与预测值对比')
plt.legend() # 显示图例
plt.grid(alpha=0.3) # 增加网格线便于观察
plt.show()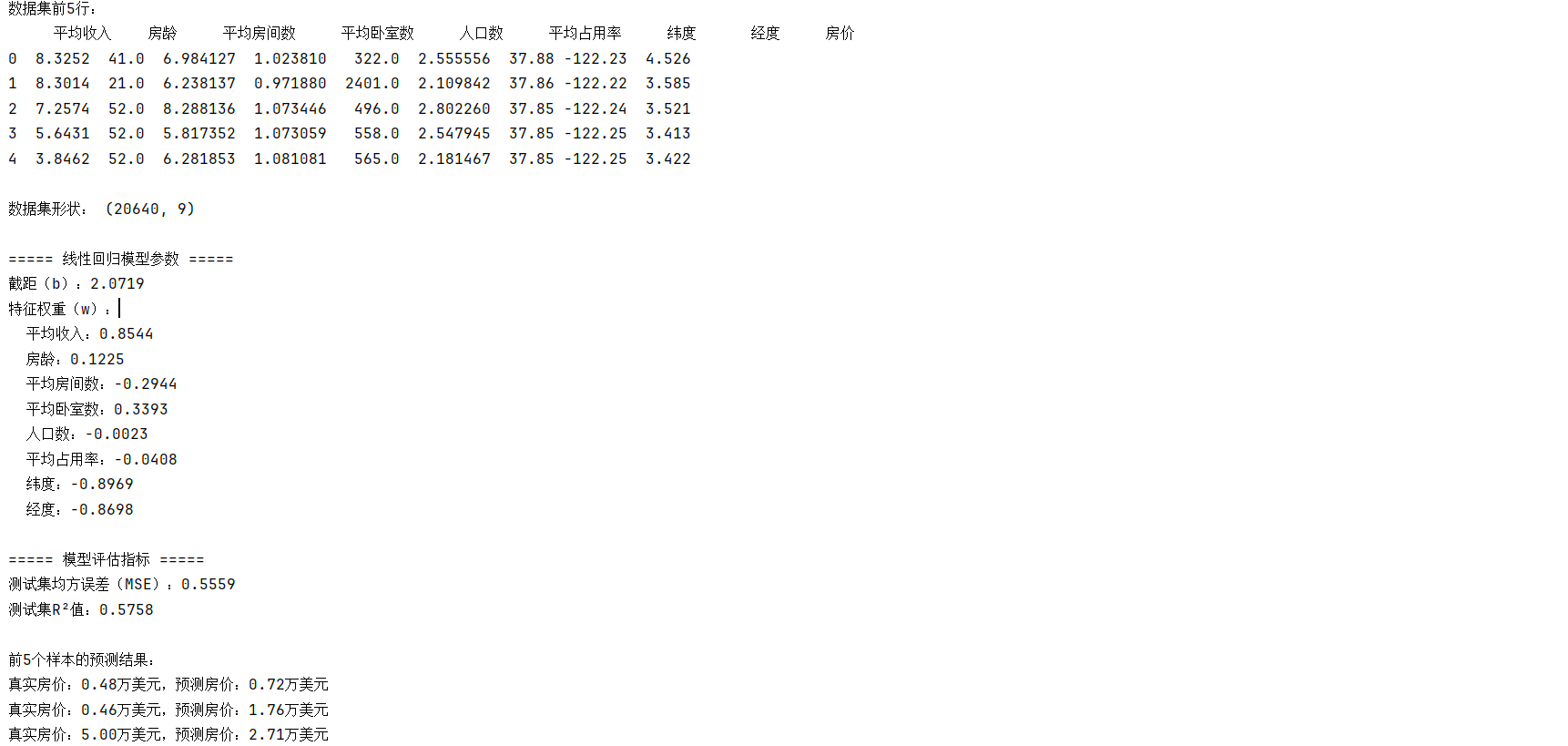
最后想说,原来机器学习不是上来就搞复杂模型,能用一条直线解决问题,本身就很有价值。明天打算试试用它预测其他数据(比如汽车油耗),看看能不能找到新的规律~
(附:代码里处理中文显示的小技巧:plt.rcParams["font.family"] = ["SimHei"] ,不然图里的中文会变成方框,踩过的坑分享给大家~)
