当前位置：首页 > news >正文

Seaborn数据可视化实战:Seaborn数据可视化入门-绘制统计图表与数据分析

news 2025/8/23 16:08:29

使用Seaborn绘制统计图表：从入门到精通

学习目标

通过本课程的学习，你将掌握如何使用Seaborn库绘制各种统计图表，包括直方图、密度图和箱形图。你将了解这些图表在数据分析中的应用，以及如何通过图表来更好地理解数据。

学习内容

1 Seaborn绘制统计图表

1.1 使用Seaborn绘制直方图

直方图是一种用于展示数据分布的图表，它通过将数据分组到不同的区间（或称为“bin”）来显示每个区间内数据点的数量。直方图对于理解数据的分布特性非常有用，例如数据是否对称、是否有异常值等。

直方图的基本概念

在统计学中，直方图是一种图形表示方法，用于展示连续变量的分布情况。它通过将数据分割成若干个区间（bins），然后计算每个区间内的数据点数量来构建。直方图的x轴表示数据的取值范围，y轴表示每个区间内的数据点数量或频率。

安装环境依赖:

%pip install seaborn

使用Seaborn绘制直方图

Seaborn库提供了distplot函数来绘制直方图。distplot函数不仅可以绘制直方图，还可以同时绘制数据的核密度估计（KDE）曲线。下面是一个简单的例子，展示如何使用Seaborn绘制直方图。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np# 生成随机数据
data = np.random.randn(1000)# 绘制直方图
sns.distplot(data, bins=30, kde=True, color='blue')# 设置图表标题和标签
plt.title('Histogram with KDE')
plt.xlabel('Value')
plt.ylabel('Frequency')# 显示图表
plt.show()

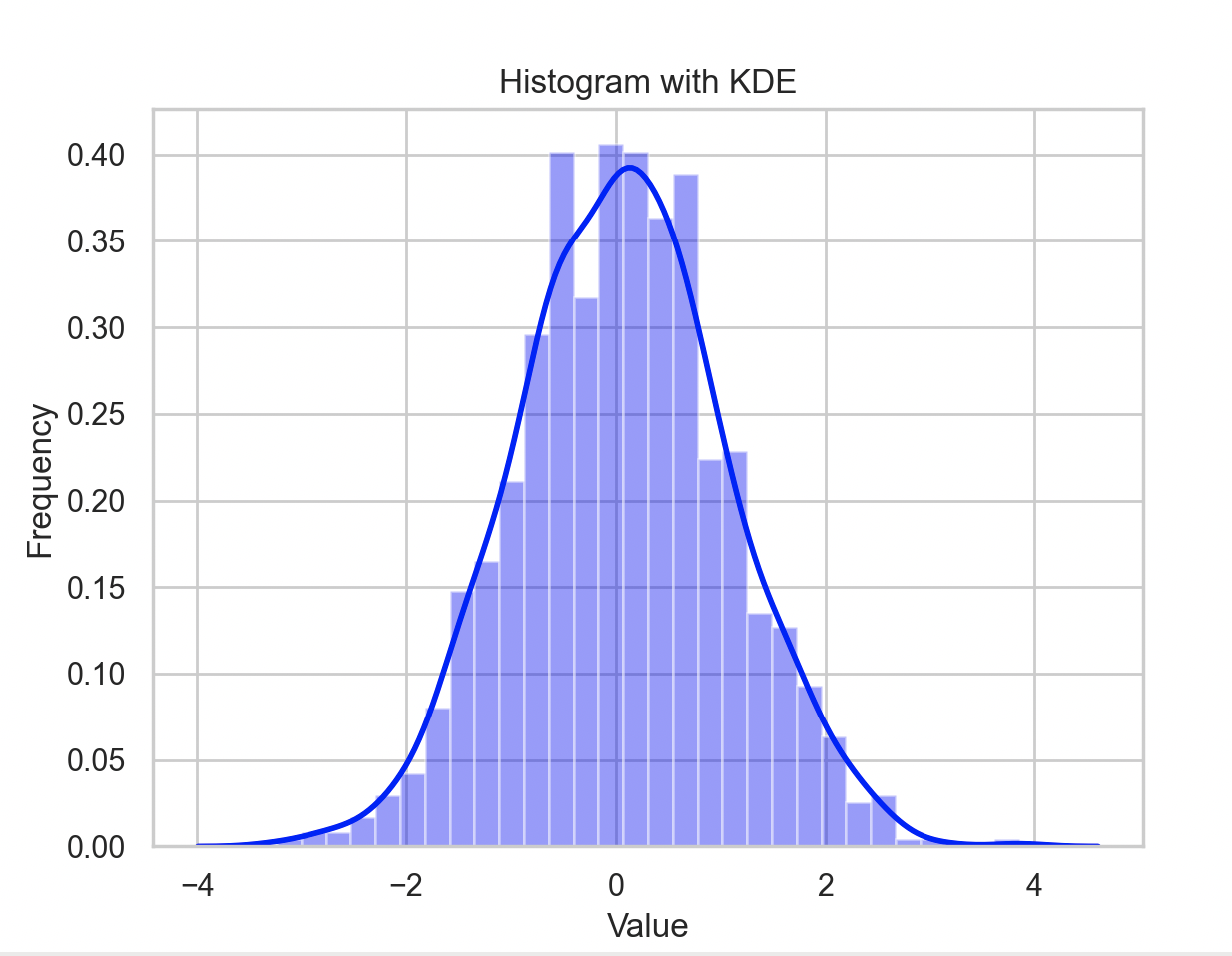
在这里插入图片描述
在这个例子中，我们首先导入了Seaborn和Matplotlib库。然后，我们生成了1000个正态分布的随机数据。使用sns.distplot函数绘制直方图，其中bins参数指定了直方图的区间数量，kde参数控制是否绘制核密度估计曲线，color参数设置了直方图的颜色。最后，我们设置了图表的标题和标签，并显示了图表。

直方图在数据分析中非常有用，特别是在以下场景中：
- 数据分布的可视化：通过直方图可以直观地看到数据的分布情况，例如数据是否对称、是否有异常值等。
- 数据预处理：在进行数据预处理时，直方图可以帮助我们发现数据中的异常值或缺失值。
- 模型评估：在机器学习中，直方图可以用于评估模型的预测结果，例如预测值的分布情况。

1.2 使用Seaborn绘制密度图

密度图是一种用于展示数据分布的平滑曲线图，它通过核密度估计（KDE）方法来估计数据的概率密度函数。密度图可以更直观地展示数据的分布情况，特别是在数据量较大时。

密度图的基本概念

密度图通过核密度估计（KDE）方法来估计数据的概率密度函数。KDE是一种非参数方法，它通过在每个数据点上放置一个核函数（如高斯核），然后将所有核函数的结果相加来得到最终的密度估计。密度图可以更直观地展示数据的分布情况，特别是在数据量较大时。

使用Seaborn绘制密度图

Seaborn库提供了kdeplot函数来绘制密度图。下面是一个简单的例子，展示如何使用Seaborn绘制密度图。

import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np# 生成随机数据
data = np.random.randn(1000)# 绘制密度图
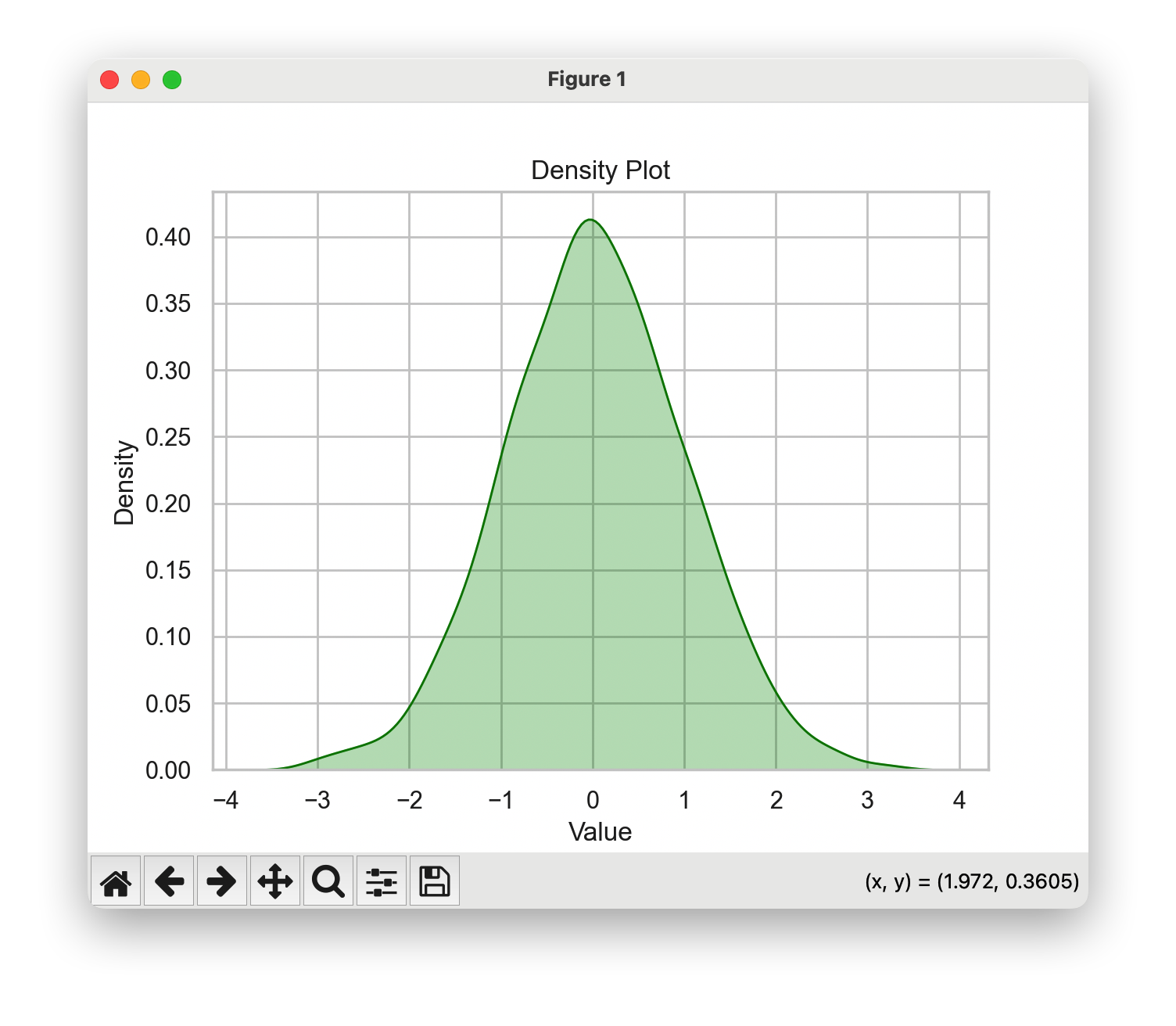
sns.kdeplot(data, shade=True, color='green')# 设置图表标题和标签
plt.title('Density Plot')
plt.xlabel('Value')
plt.ylabel('Density')# 显示图表
plt.show()

在这个例子中，我们使用sns.kdeplot函数绘制密度图。shade参数控制是否填充密度曲线下的区域，color参数设置了密度曲线的颜色。最后，我们设置了图表的标题和标签，并显示了图表。

密度图在数据分析中非常有用，特别是在以下场景中：
- 数据分布的平滑展示：密度图可以更平滑地展示数据的分布情况，特别是在数据量较大时。
- 多变量分布的比较：通过绘制多个变量的密度图，可以直观地比较不同变量的分布情况。
- 异常值检测：密度图可以帮助我们发现数据中的异常值，特别是在数据分布的尾部。

在这里插入图片描述

1.3 使用Seaborn绘制箱形图

箱形图是一种用于展示数据分布的图表，它通过五个统计量（最小值、第一四分位数、中位数、第三四分位数和最大值）来描述数据的分布情况。箱形图对于识别数据中的异常值非常有用。

箱形图通过五个统计量来描述数据的分布情况：
最小值：数据中的最小值。
第一四分位数（Q1）：数据中25%的数据小于或等于这个值。
中位数（Q2）：数据中50%的数据小于或等于这个值。
第三四分位数（Q3）：数据中75%的数据小于或等于这个值。
最大值：数据中的最大值。
箱形图中的“箱”表示第一四分位数到第三四分位数之间的范围，箱内的横线表示中位数。箱形图的“胡须”表示数据的最小值和最大值，超出胡须范围的点被认为是异常值。
使用Seaborn绘制箱形图
Seaborn库提供了boxplot函数来绘制箱形图。下面是一个简单的例子，展示如何使用Seaborn绘制箱形图。

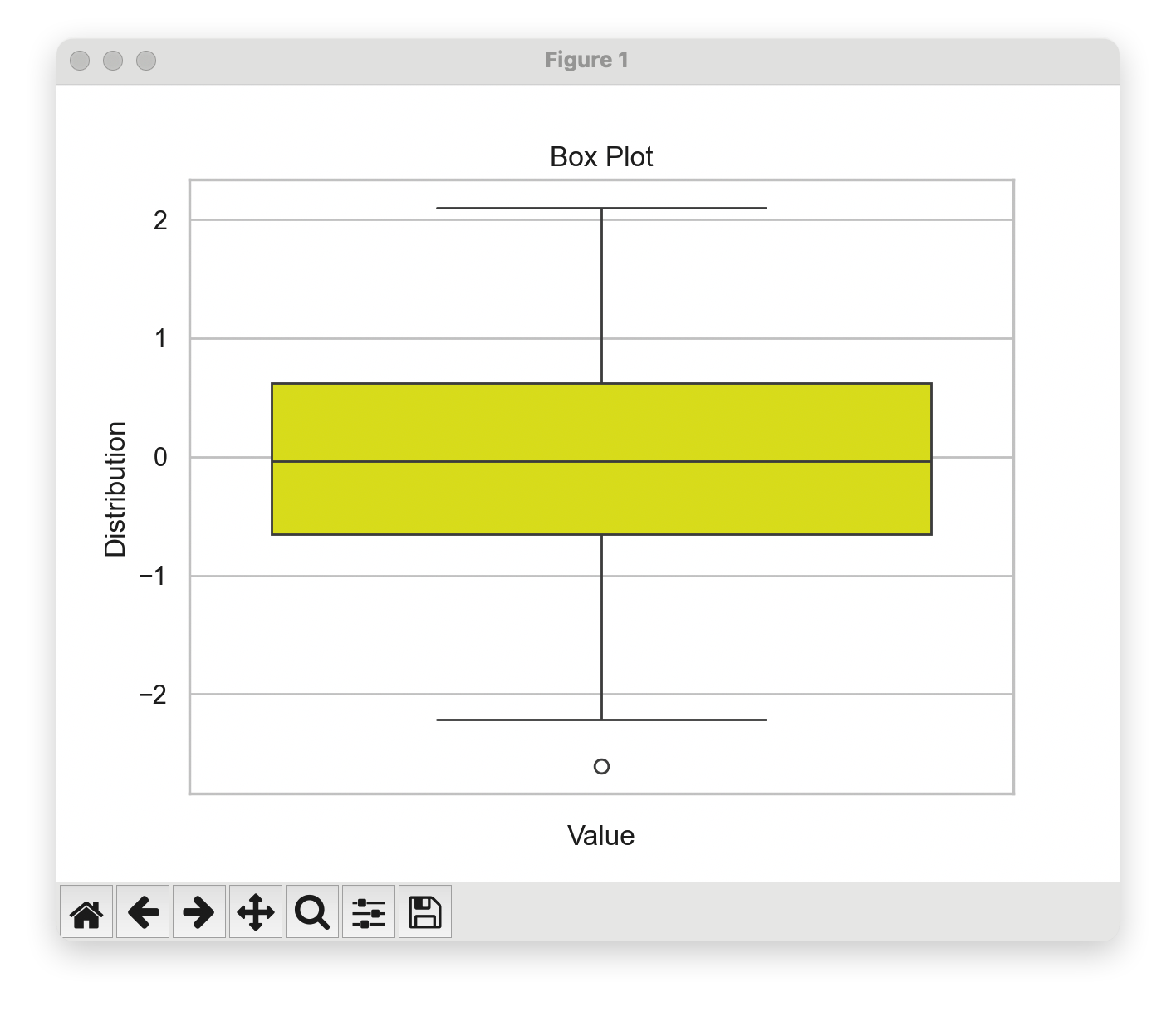
在这个例子中，我们使用sns.boxplot函数绘制箱形图。color参数设置了箱形图的颜色。最后，我们设置了图表的标题和标签，并显示了图表。