小杰机械视觉(three day)——图象旋转、镜像、缩放、矫正
1.图象旋转
所有像素点围绕某点旋转一定角度的图案,
围绕任意点进行旋转
(1)仿射变换
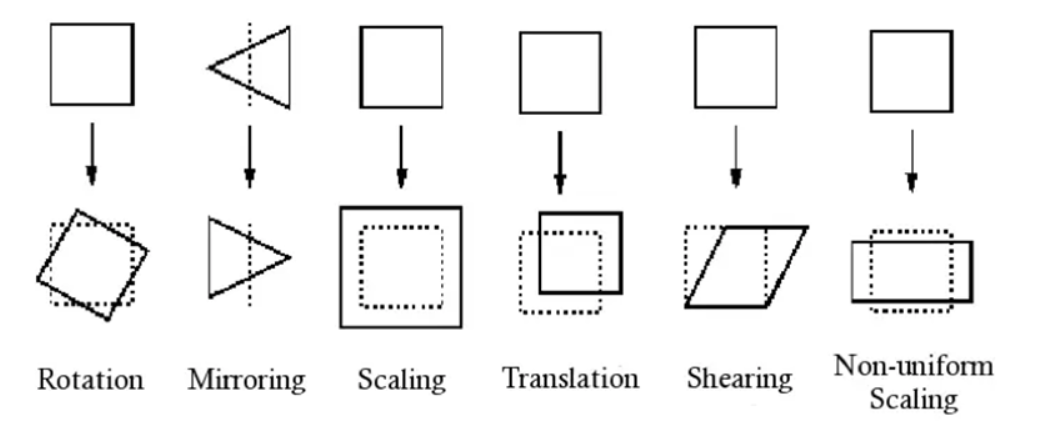
仿射变换可以分为 单点旋转+平移
旋转矩阵:
![]()
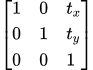
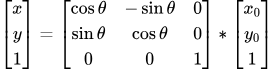
阵的乘法是有顺序的

仿射变换矩阵:
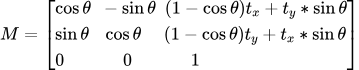
- 平直性
直线在经过变换后还是直线。
- 平行性
平行线在经过变换后还是平行线。
- angle 旋转角度,正数为逆时针,负数为顺时针。
- scale:缩放比例,先设置为1,后续讲解图像缩放原理
(2)插值方法
旋转过程中可能会出现的问题:
1. 取整丢失精度
2. 缩放丢失精度。
五种常见的插值算法:
1.最近邻插值:
速度最快,但是可能会导致图像出现锯齿状边缘(马赛克)和失真。
2.双线性插值:
相比于最近邻插值计算速度稍慢,但是效果大幅提升,适用于绝大多数场景。
3.像素区域插值:
更适合缩小图像且保持质量时使用。
4.双三次插值:
速度很慢,但是效果很好。
5.Lanczos(兰克索斯)插值:
速度最慢,效果最好。
1.最近邻插值 INTER_NEAREST
以图片放大为例,dst表示放大后的目标图像,src表示放大前的原图。

上面的公式的目的是让dst图像的每个像素值都对应到src原图的某个像素值,例如从一个2*2的图像放大到4*4的过程如下:
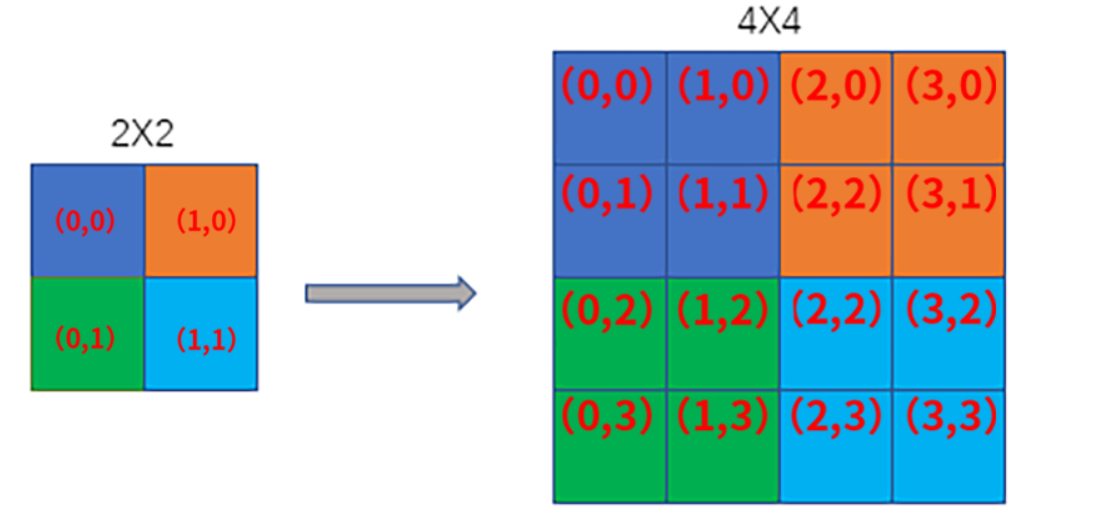
对应的是原图src的(0.5, 0)像素点,OpenCV固定向下取整,取整后为![]() 。
。
全图像素点依次计算,得到完整的dst图像。
2.双线性插值 INTER_LINEAR
双线性插值算法是一种比较好的图像缩放算法,它充分利用了原图src中虚拟点四周的四个真实像素点来推算dst图中的一个像素点的值。因此效果比较好,不会出现不连续的情况。
3.线性插值
假如已知两个点(x0,y0)和(x1,y1),计算两个点之间的某个位置x在直线上的y值,过程为:
![]()
已知x求y:
![]()
上面的过程就是一个线性插值,双线性插值本质上就是在两个方向上进行线性插值。
4.双线性插值

假设根据上述公式计算出了dst中某个点对应的点P(通常是个小数),所以在周围会有四个原始图像的像素点(左上Q12、右上Q22、左下Q11、右下Q21)包围。
第一个方向的单线性插值:
先根据Q12和Q22计算单线性插值R2的像素值,再计算Q11和Q21单线性插值R1的像素值。
第二个方向的单线性插值:
根据上一步计算出的R1和R2,再进行一次单线性插值,得到P点的像素值
5.双线性插值的问题
1.不同位置的像素点处理不公平。
无论采取什么坐标系,都会发现src的原点会直接复制到dst中;而有些边界的像素点相当于只进行了1次单线性插值。
2. 整体图像的相对位置会发生变化
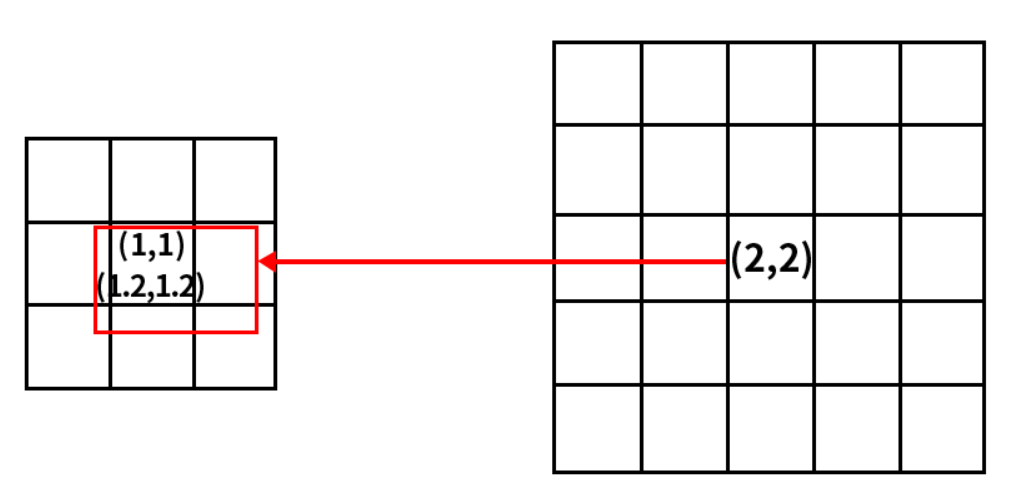
如下图所示,左侧为src原图,右侧为dst目标图像,源图像的几何中心像素点坐标为(1,1),但是目标图像的几何中心点为(2,2)。根据点和点的对应关系,目标图像的集合中心点应该为(1.2,1.2)。
按照之前的坐标系,原图与目标图像应该是原点重合,因此目标图像的几何中心点相对于原始图像的几何中心点偏向于右下角。
因此在OpenCV中,为了解决上面的问题,对公式进行了优化,如下:
![]()
![]()
了解部分
3.像素区域插值 INTER_AREA
像素区域插值主要分为两种情况:缩小图像和放大图像的原理并不相同。
1. 缩小图像
内部会使用一个均值滤波器(滤波器就是一个核,后续实验会介绍),其工作原理可以理解为对一个区域内的像素考虑核之后进行平均。
2. 放大图像
- 如果放大的是整数倍
与最近邻插值类似
- 如果放大的不是整数倍
直接使用双线性插值
4.双三次插值 INTER_CUBIC
与双线性插值类似,该方法也是通过映射,在映射点的邻域内通过加权来的到放大图像的像素值。不同的是双三次插值法需要源图像src中近邻的16个像素点来进行加权。
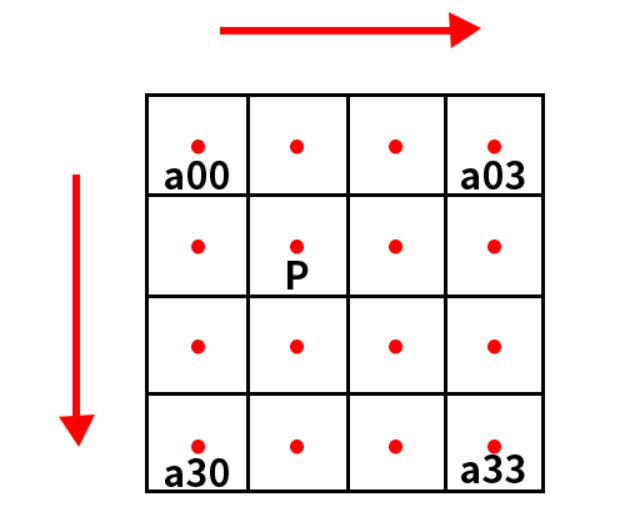
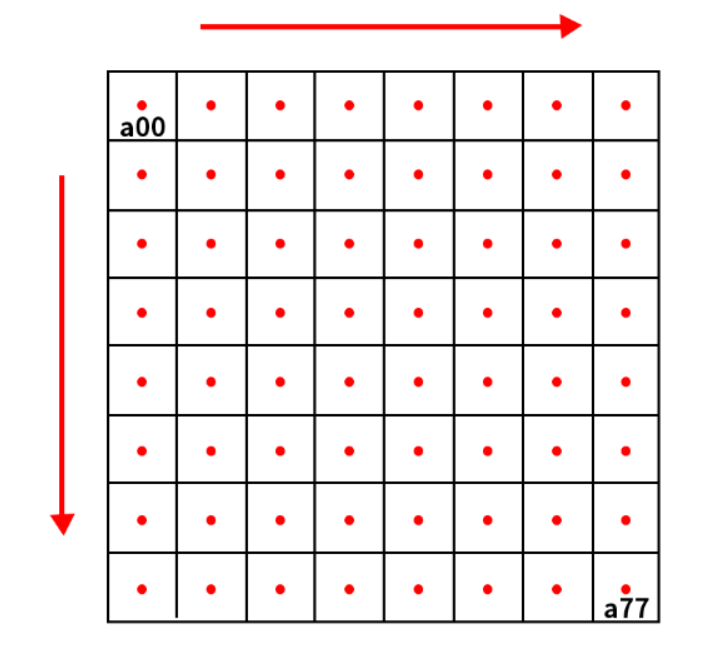
以上图为例,假设源图像src的大小为m*n,缩放之后的目标图像dst大小为M*N,其中src的每个像素点是已知的,目标图像dst是未知的,需要求出dst中每个像素点(X,Y)的值。
必须先找出像素B(X,Y)在源图像中对应的像素(x,y),再根据(x,y)在原图src中最近的16个像素点作为计算(X,Y)的参数,利用BiCubic基函数求出16个像素点的权重,dst中(X,Y)的值就是src中16个像素点的加权求和。
BiCubic函数:
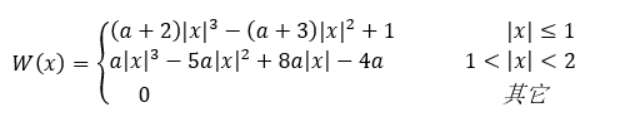
假设上图中的P点就是dst在(X,Y)处根据公式计算出的对应源图像src的位置,P的坐标(x+u,y+v)会出现小数部分,x,y表示整数部分,u,v表示小数部分,利用a00、a01......表示需要加权的16个像素点。
需要把16个像素点的整数部分和小数部分分别带入到BiCubic函数中(最终整数部分和小数部分权重相加),求出每个像素点的权重W,需要注意的是变量a经过试验通常取-0.5或-0.75。
剩下的变量只有x,但是a00等点的坐标是二维,需要把a00等点的x和y分别拆开带入BiCubic函数中计算。
例如,计算a00点的权重:
先把x=0带入BiCubic函数中,求出x方向权重W(i);
再把y=0带入BiCubic函数总,求出y方向的权重W(j)。
相乘得到最终权重,计算所有16个点的权重,公式如下:
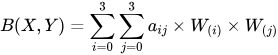
5.Lanczos插值 INTER_LANCZOS4
Lanczos插值方法与双三次插值的思想是一样,不同的是近邻的像素点范围变成了8*8,并且换了一个公式来计算像素点的权重。
权重公式换为:

其他的计算过程与双三次插值完全相同,最终的权重公式为:
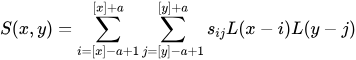
(3)边界填充
1.边界复制 BORDER_REPLICATE
边界复制会将边界处的像素值进行复制,然后作为边界填充的像素值,如下图所示,可以看到四周的像素值都一样。

2.边界反射 BORDER_REFLECT

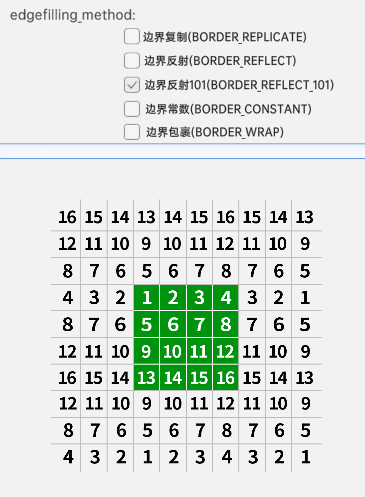
3.边界反射101 BORDER_REFLECT_101
与边界反射的区别是,不再反射边缘像素的点。
4.边界常数 BORDER_CONSTANT
边界常数表示补充一个自定义的像素值,下图虚拟仿真节点中的参数为补充的像素的BGR通道值。
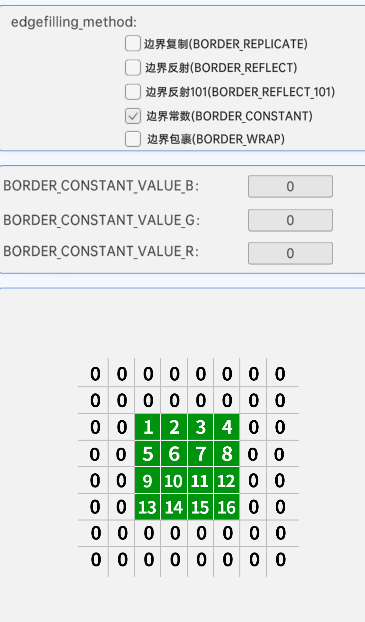
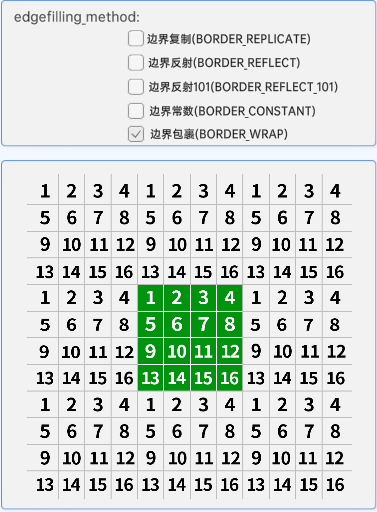
5.边界包裹 BORDER_WRAP
与边界反射的区别是不再进行轴对称。
(4)代码
import cv2
import numpy as npif __name__ == '__main__':# 1. 图片输入path = 'lena.png'image_np = cv2.imread(path)# 2. 单点旋转 + 图片旋转,相当于直接构建复合矩阵angle = 45 # 旋转角scale = 2 # 缩放比例# 获得二维旋转的仿射变换矩阵M = cv2.getRotationMatrix2D((0, 0), # 旋转点angle, # 旋转角度scale # 缩放比例)print(M)# 4. 插值方法 + 5. 边缘填充# 仿射变换rotation_image = cv2.warpAffine(image_np, # 图像M, # 仿射变换矩阵(image_np.shape[1] * 2, image_np.shape[0] * 2), # 目标图像的分辨率flags=cv2.INTER_LANCZOS4, # 插值方法borderMode=cv2.BORDER_WRAP # 边界填充)# 6. 图片输出cv2.imshow('rotation_image', rotation_image)cv2.imwrite('rotation_image.png', rotation_image)cv2.waitKey(0)
2.图象镜像
图像的镜像旋转分为三种,分别使用filpcode的参数表示:
- flipcode=0,垂直翻转
垂直翻转可以把src沿着x轴翻转,坐标从(x,y)翻转为(x,-y)。
- flipcode>0,水平翻转
水平翻转可以把src沿着y轴翻转,坐标从(x,y)翻转为(-x,y)。
- flipcode<0,水平垂直翻转
相当与图像旋转,x轴和y轴都翻转,坐标从(x,y)翻转为(-x,-y)。
代码
import cv2
import numpy as npif __name__ == '__main__':# 1. 图片输入path = 'lena.png'image_np = cv2.imread(path)# 2. 图片镜像旋转flip_image = cv2.flip(image_np, # 要反转的图像-1, # 翻转码)# 3. 图片输出cv2.imshow('flip_image',flip_image)cv2.waitKey(0)
3.图象缩放
图像缩放相比之前图像旋转实验中,可以单独针对x轴和y轴进行独立的倍率缩放,另外插值方法节点与图像缩放实验完全相同。
代码
import cv2
import numpy as npif __name__ == '__main__':# 1. 图片输入path = 'lena.png'image_np = cv2.imread(path)# 2. 图像缩放+3. 插值方法resize_image = cv2.resize(image_np, # 原图(0, 0), # 目标分辨率(宽高),如果设置这个参数,x轴和y轴的缩放比例失效fx=2, # x轴倍率fy=0.5, # y轴倍率interpolation=cv2.INTER_LINEAR # 插值方法)# 4. 图片输出cv2.imshow('resize_image', resize_image)cv2.waitKey(0)
4.图象矫正
(1)仿射变换与透视变换
仿射变换
之前在图像旋转实验中已经接触过仿射变换,仿射变换是一个二维坐标系到另一个二维坐标系的过程,在仿射变换中符合直线的平直性和平行性。
透视变换
透视变换是把一个图像投影到一个新的视平面的过程。在现实世界中,观察到的物体在人类视觉中都会受到透视效果的影响:近大远小。
1.透视变换矩阵
与仿射变换相同,透视变换也有对应的透视变换矩阵,在这个过程原始图像src中的点(x,y)通过透视变换被转换到到dst图像中的新坐标点(x',y')
变换过程如下:

它将原始图像的齐次坐标(x,y,1)变换为目标图像齐次坐标的(X,Y,Z),可以推导出:
![]()
![]()
![]()
Z是三维坐标,但是dst是二维图像,此需要把三维的Z消除(除以Z),可以得到新的表达式:
![]()
![]()
a11,a12,...,a33表示一些旋转量和平移量,涉及到三维图像学的变换,因此不去详细研究,只要理解过程就行。
使用上面的透视变换矩阵需要给算法提供输入的数据,通过输入数据计算a11,a12,...,a33的值,此处提供的输入数据必须满足以下条件:
- 在源图像src中选择四个点
- 不能共线
- 四个点要符合透视变换关系(来自于摄像头)
代码

import cv2
import numpy as npif __name__ == '__main__':# 1. 图片输入path = 'card.png'image_np = cv2.imread(path)# 2. 坐标选取# 左上、右上、左下、右下points = [[110, 60], [330, 88], [72, 185], [320, 220]]# 转换为np数组pts1 = np.float32(points) # src的四个角点print(pts1)print(type(pts1))# 画红框,标记ROI区域image_line = image_np.copy()# 画四条线cv2.line(image_line, # 在哪个图像上画线points[0], # 起点points[1], # 终点(0, 0, 255), # 颜色2, # 粗度cv2.LINE_AA # 抗锯齿)cv2.line(image_line, # 在哪个图像上画线points[1], # 起点points[3], # 终点(0, 0, 255), # 颜色2, # 粗度cv2.LINE_AA # 抗锯齿)cv2.line(image_line, # 在哪个图像上画线points[2], # 起点points[3], # 终点(0, 0, 255), # 颜色2, # 粗度cv2.LINE_AA # 抗锯齿)cv2.line(image_line, # 在哪个图像上画线points[0], # 起点points[2], # 终点(0, 0, 255), # 颜色2, # 粗度cv2.LINE_AA # 抗锯齿)# 3. 获取透视变换矩阵# 获得原图分辨率img_shape = image_np.shape# 左上、右上、左下、右下points = [[0, 0], [img_shape[1], 0], [0, img_shape[0]], [img_shape[1], img_shape[0]]]print(points)# 转换为np数组pts2 = np.float32(points) # dst的四个角点# 生成透视变换矩阵M = cv2.getPerspectiveTransform(pts1, # src的四个角点pts2 # dst的四个角点)print(M)# 4. 透视变换 + 5. 插值方法 + 6. 边缘填充correct_image = cv2.warpPerspective(image_np, # 原图M, # 透视变换矩阵(img_shape[1], img_shape[0]), # dst分辨率cv2.INTER_LINEAR, # 插值方法cv2.BORDER_WRAP # 边缘填充)# 7. 图片输出cv2.imshow('image_line', image_line)cv2.imshow('correct_image', correct_image)cv2.waitKey(0)
