【大语言模型 14】Transformer权重初始化策略：从Xavier到GPT的参数初始化演进之路

【大语言模型 14】Transformer权重初始化策略：从Xavier到GPT的参数初始化演进之路

关键词：Transformer权重初始化、Xavier初始化、He初始化、预训练模型权重、训练收敛速度、梯度流动、参数初始化策略、深度学习优化

摘要：权重初始化是深度学习训练成功的隐秘基石，特别是在Transformer这样的深层架构中，合适的初始化策略能够决定模型的训练稳定性和收敛速度。本文从经典的Xavier和He初始化出发，深入解析Transformer特有的初始化策略，通过数学推导、代码实现和实验分析，揭示不同初始化方法对大语言模型训练的深层影响。我们将探讨为什么GPT系列模型采用特定的初始化方案，以及如何针对不同层设计最优的初始化策略。

引言：为什么权重初始化如此重要？

想象一下，你要训练一个拥有数十亿参数的Transformer模型。在开始训练的那一刻，这些参数的初始值将决定模型能否成功收敛。如果初始化不当，可能出现梯度爆炸、梯度消失，或者训练速度极其缓慢的问题。

权重初始化看似是一个技术细节，实际上是决定深度学习成功的关键因素之一。特别是在Transformer架构中，由于其深层结构和复杂的注意力机制，权重初始化的重要性更加凸显。

让我问你一个问题：为什么不能将所有权重都初始化为0？如果都是0，那么每一层的所有神经元都会输出相同的值，梯度也会相同，这种对称性会使得神经网络无法学习到不同的特征表示。

那么，应该如何打破这种对称性，同时保证训练的稳定性呢？这就是权重初始化要解决的核心问题。

经典初始化方法回顾

Xavier初始化：对称激活函数的最优选择

Xavier初始化（也称为Glorot初始化）是2010年由Xavier Glorot提出的经典方法。其核心思想是保持前向传播和反向传播过程中信号的方差稳定。

数学原理推导：

假设输入$x$的各个分量是独立同分布的，方差为$Var(x)$。对于线性变换$y=Wx+b$，如果权重$W$的各个分量也是独立同分布的，且均值为0，那么：

$$Var(y)=n_{in}\cdot Var(W)\cdot Var(x)$$

其中$n_{in}$是输入维度。

为了保持$Var(y)=Var(x)$，需要：
$$Var(W)=\frac{1}{n_{in}}$$

同时考虑反向传播，为了保持梯度方差稳定，需要：
$$Var(W)=\frac{1}{n_{out}}$$

Xavier初始化取两者的调和平均：
$$Var(W)=\frac{2}{n_{in}+n_{out}}$$

在实际实现中，Xavier初始化有两种形式：

import torch
import torch.nn as nn
import math# Xavier均匀分布初始化
def xavier_uniform_init(tensor):fan_in = tensor.size(-1)fan_out = tensor.size(0)std = math.sqrt(6.0 / (fan_in + fan_out))with torch.no_grad():tensor.uniform_(-std, std)# Xavier正态分布初始化
def xavier_normal_init(tensor):fan_in = tensor.size(-1)fan_out = tensor.size(0)std = math.sqrt(2.0 / (fan_in + fan_out))with torch.no_grad():tensor.normal_(0, std)

He初始化：ReLU激活函数的福音

He初始化由何凯明等人在2015年提出，专门针对ReLU激活函数进行优化。ReLU函数会将负数部分置零，这意味着大约一半的神经元被"杀死"，有效的扇入数量减少了一半。

数学推导：

对于ReLU激活函数，由于输出的一半被置零，有效方差变为：
$$Var(y)=\frac{1}{2}\cdot n_{in}\cdot Var(W)\cdot Var(x)$$

为了保持$Var(y)=Var(x)$，需要：
$$Var(W)=\frac{2}{n_{in}}$$

He初始化的实现：

# He均匀分布初始化
def he_uniform_init(tensor):fan_in = tensor.size(-1)std = math.sqrt(6.0 / fan_in)with torch.no_grad():tensor.uniform_(-std, std)# He正态分布初始化
def he_normal_init(tensor):fan_in = tensor.size(-1)std = math.sqrt(2.0 / fan_in)with torch.no_grad():tensor.normal_(0, std)

两种方法的适用场景

• Xavier初始化：适用于tanh、sigmoid等对称激活函数
• He初始化：适用于ReLU、Leaky ReLU等非对称激活函数

但是在Transformer中，我们主要使用GELU、ReLU或Swish等激活函数，情况变得更加复杂。

Transformer特有的初始化挑战

注意力机制的初始化难题

Transformer中的自注意力机制引入了新的复杂性。在多头注意力中，查询（Q）、键（K）、值（V）矩阵的初始化直接影响注意力权重的分布。

让我们考虑注意力权重的计算：
$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

如果Q和K的初始化不当，$Q{K}^T$的值可能过大或过小，导致：

1. 过大：softmax饱和，注意力过于集中
2. 过小：注意力分布过于平均，失去选择性

深度网络的梯度传播问题

Transformer通常有12-96层，这种深度带来了严重的梯度传播问题。即使每层的方差变化很小，累积效应也会导致梯度爆炸或消失。

假设每层的梯度方差缩放因子为$\alpha$，那么$L$层网络的总缩放因子为${\alpha }^L$。即使$\alpha =1.1$，在24层网络中，梯度也会放大$(1.1{)}^{24}\approx 9.8$倍。

残差连接的影响

Transformer中的残差连接改变了信号传播的动态特性。残差路径$y=F(x)+x$中，如果$F(x)$的方差与$x$相当，那么输出方差约为输入的两倍。

class TransformerBlock(nn.Module):def __init__(self, d_model, n_heads):super().__init__()self.attention = MultiHeadAttention(d_model, n_heads)self.ff = FeedForward(d_model)self.norm1 = nn.LayerNorm(d_model)self.norm2 = nn.LayerNorm(d_model)# 关键：初始化策略影响残差连接的稳定性self._init_weights()def _init_weights(self):# 这里的初始化策略至关重要passdef forward(self, x):# 残差连接1x = x + self.attention(self.norm1(x))# 残差连接2  x = x + self.ff(self.norm2(x))return x

GPT系列的初始化策略解析

GPT-1的初始化方案

GPT-1采用了相对简单的初始化策略：

def gpt1_init_weights(module):if isinstance(module, nn.Linear):# 使用正态分布初始化，标准差为0.02module.weight.data.normal_(mean=0.0, std=0.02)if module.bias is not None:module.bias.data.zero_()elif isinstance(module, nn.Embedding):module.weight.data.normal_(mean=0.0, std=0.02)

这个看似简单的策略实际上有深层考虑：

• 小标准差（0.02）：避免梯度爆炸
• 统一标准差：简化超参数调优

GPT-2/3的改进策略

GPT-2引入了更精细的初始化策略：

def gpt2_init_weights(module):if isinstance(module, nn.Linear):# 不同层采用不同的初始化策略std = 0.02if hasattr(module, 'scale_by_depth'):# 根据深度缩放初始化标准差std = 0.02 / math.sqrt(2 * module.layer_id)module.weight.data.normal_(mean=0.0, std=std)if module.bias is not None:module.bias.data.zero_()elif isinstance(module, nn.Embedding):module.weight.data.normal_(mean=0.0, std=0.02)

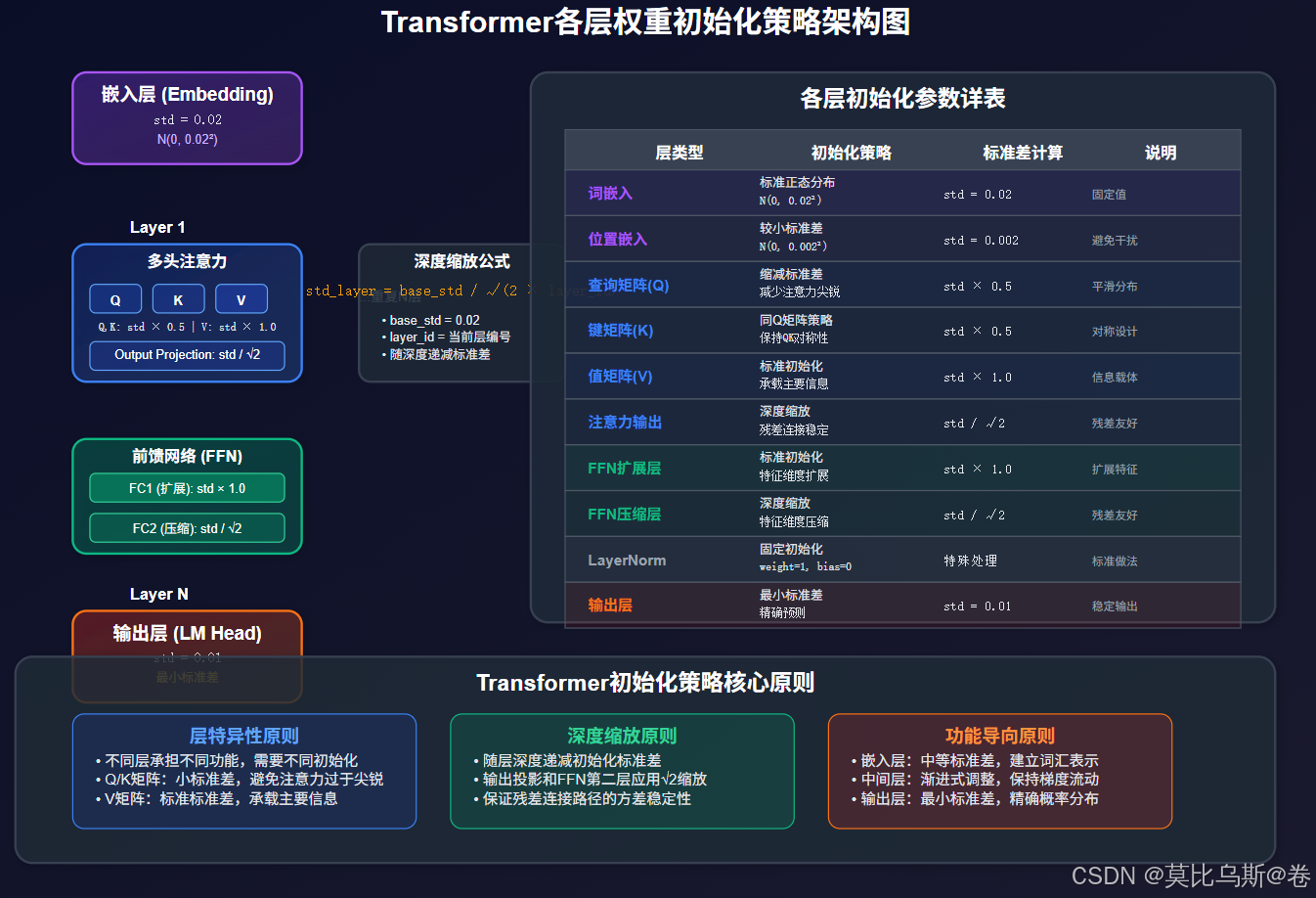
层特异性初始化策略

不同类型的层需要不同的初始化策略：

class AdvancedTransformerInit:@staticmethoddef init_attention_weights(attention_layer, d_model):"""注意力层的特殊初始化"""std = math.sqrt(2.0 / d_model)# Q, K矩阵使用较小的标准差attention_layer.query.weight.data.normal_(0, std * 0.5)attention_layer.key.weight.data.normal_(0, std * 0.5)# V矩阵使用标准标准差attention_layer.value.weight.data.normal_(0, std)# 输出投影层使用深度缩放attention_layer.out_proj.weight.data.normal_(0, std / math.sqrt(2))@staticmethoddef init_feedforward_weights(ff_layer, d_model, d_ff):"""前馈网络的初始化"""# 第一层：扩展层std1 = math.sqrt(2.0 / d_model)ff_layer.linear1.weight.data.normal_(0, std1)# 第二层：压缩层，使用更小的标准差std2 = math.sqrt(2.0 / d_ff)ff_layer.linear2.weight.data.normal_(0, std2 / math.sqrt(2))@staticmethoddef init_embedding_weights(embedding_layer):"""嵌入层的初始化"""std = 0.02embedding_layer.weight.data.normal_(0, std)# 特殊处理：位置编码可能需要更小的初始化if hasattr(embedding_layer, 'position_embeddings'):embedding_layer.position_embeddings.weight.data.normal_(0, std * 0.1)

初始化对训练收敛的影响分析

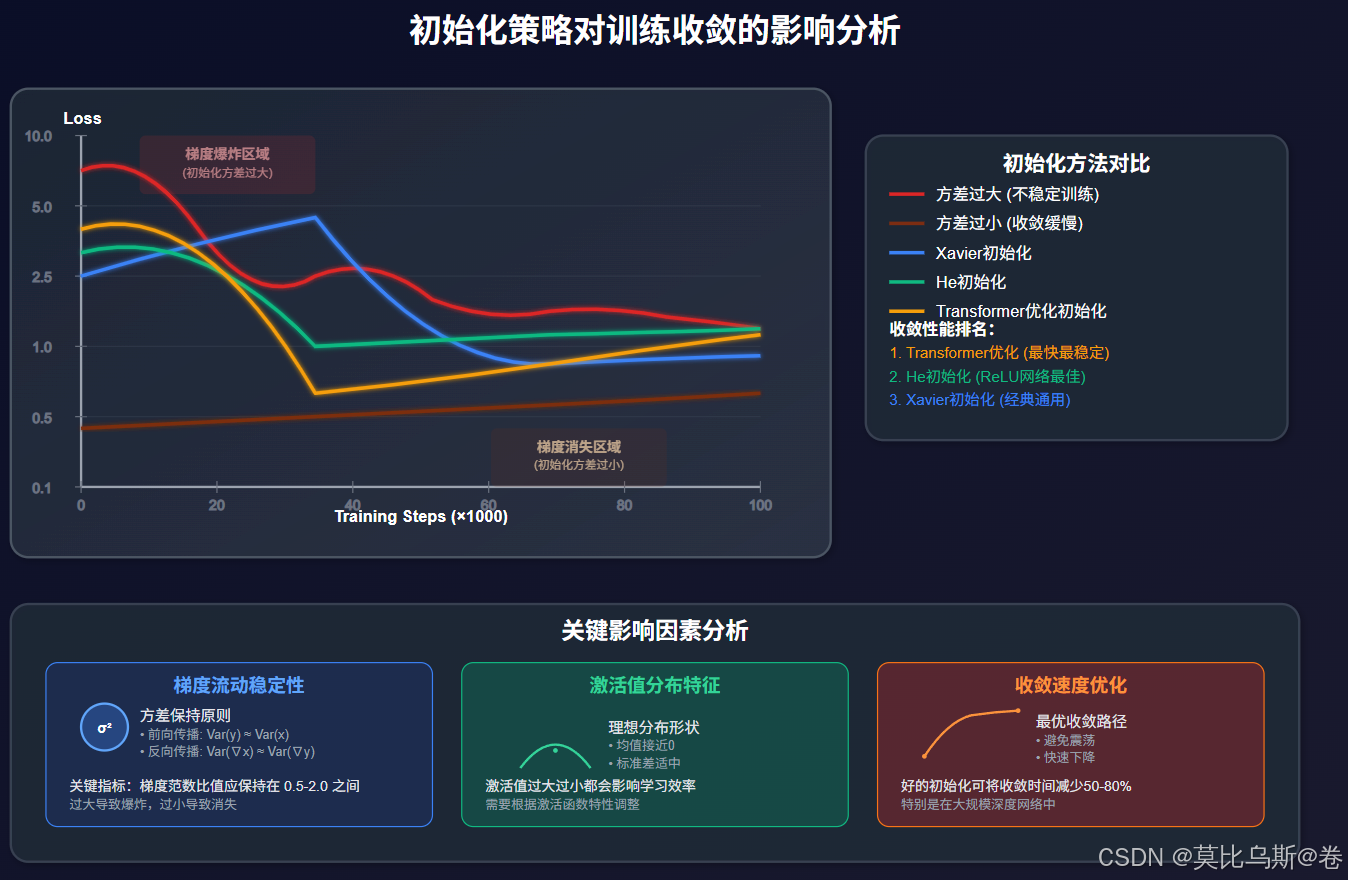
理论分析：方差传播

在深度网络中，信号的方差在前向传播和反向传播过程中的变化直接影响训练稳定性。

前向传播方差分析：

对于第$l$层，假设输入$x^{(l)}$的方差为${\sigma }_{x,l}^2$，权重$W^{(l)}$的方差为${\sigma }_{w,l}^2$，则输出方差为：

$${\sigma }_{y,l}^2=n_l\cdot {\sigma }_{w,l}^2\cdot {\sigma }_{x,l}^2$$

其中$n_l$是该层的输入维度。

反向传播方差分析：

梯度的方差传播遵循类似规律：
$${\sigma }_{\nabla x,l}^2=m_l\cdot {\sigma }_{w,l}^2\cdot {\sigma }_{\nabla y,l}^2$$

其中$m_l$是该层的输出维度。

实验验证：不同初始化的收敛对比

让我们通过实验来验证不同初始化策略的效果：

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as npclass SimpleTransformer(nn.Module):def __init__(self, d_model=512, n_layers=6, init_method='xavier'):super().__init__()self.layers = nn.ModuleList([nn.Linear(d_model, d_model) for _ in range(n_layers)])self.init_method = init_methodself._init_weights()def _init_weights(self):for i, layer in enumerate(self.layers):if self.init_method == 'xavier':nn.init.xavier_normal_(layer.weight)elif self.init_method == 'he':nn.init.kaiming_normal_(layer.weight)elif self.init_method == 'gpt':layer.weight.data.normal_(0, 0.02)elif self.init_method == 'scaled':std = 0.02 / math.sqrt(2 * (i + 1))layer.weight.data.normal_(0, std)def forward(self, x):activations = []for layer in self.layers:x = torch.relu(layer(x))activations.append(x.var().item())return x, activations# 比较不同初始化方法
def compare_initializations():torch.manual_seed(42)x = torch.randn(100, 512)methods = ['xavier', 'he', 'gpt', 'scaled']results = {}for method in methods:model = SimpleTransformer(init_method=method)with torch.no_grad():_, activations = model(x)results[method] = activations# 可视化结果plt.figure(figsize=(12, 8))for method, activations in results.items():plt.plot(range(1, 7), activations, 'o-', label=method, linewidth=2)plt.xlabel('Layer Depth')plt.ylabel('Activation Variance')plt.title('Activation Variance Across Layers')plt.legend()plt.grid(True, alpha=0.3)plt.show()return results# 运行比较
variance_results = compare_initializations()

梯度流动分析

初始化策略对梯度流动有直接影响。我们可以通过分析梯度范数来评估训练稳定性：

def analyze_gradient_flow(model, loss_fn, input_data, target):"""分析梯度在各层中的流动情况"""model.train()model.zero_grad()output = model(input_data)loss = loss_fn(output, target)loss.backward()gradients = []layer_names = []for name, param in model.named_parameters():if param.grad is not None:gradients.append(param.grad.norm().item())layer_names.append(name)return layer_names, gradients# 梯度流动可视化
def plot_gradient_flow(layer_names, gradients):plt.figure(figsize=(15, 6))plt.plot(range(len(gradients)), gradients, 'b.-', linewidth=2)plt.xlabel('Layer')plt.ylabel('Gradient Norm')plt.title('Gradient Flow Across Layers')plt.xticks(range(len(layer_names)), layer_names, rotation=45)plt.grid(True, alpha=0.3)plt.tight_layout()plt.show()

预训练模型的权重分析

权重分布的统计特性

通过分析成功训练的大型预训练模型，我们可以了解理想的权重分布特征：

def analyze_pretrained_weights(model_name='gpt2'):"""分析预训练模型的权重分布"""from transformers import GPT2Modelmodel = GPT2Model.from_pretrained(model_name)weight_stats = {}for name, param in model.named_parameters():if 'weight' in name:stats = {'mean': param.data.mean().item(),'std': param.data.std().item(),'min': param.data.min().item(),'max': param.data.max().item(),'shape': param.shape}weight_stats[name] = statsreturn weight_stats# 分析权重分布
def plot_weight_distributions(weight_stats):"""可视化权重分布"""fig, axes = plt.subplots(2, 2, figsize=(15, 10))# 提取统计数据stds = [stats['std'] for stats in weight_stats.values()]means = [stats['mean'] for stats in weight_stats.values()]layer_names = list(weight_stats.keys())# 标准差分布axes[0, 0].hist(stds, bins=20, alpha=0.7)axes[0, 0].set_title('Weight Standard Deviation Distribution')axes[0, 0].set_xlabel('Standard Deviation')# 均值分布axes[0, 1].hist(means, bins=20, alpha=0.7)axes[0, 1].set_title('Weight Mean Distribution')axes[0, 1].set_xlabel('Mean')# 层级标准差变化axes[1, 0].plot(range(len(stds)), stds, 'o-')axes[1, 0].set_title('Standard Deviation Across Layers')axes[1, 0].set_xlabel('Layer Index')axes[1, 0].set_ylabel('Standard Deviation')# 权重范围weight_ranges = [stats['max'] - stats['min'] for stats in weight_stats.values()]axes[1, 1].plot(range(len(weight_ranges)), weight_ranges, 'o-')axes[1, 1].set_title('Weight Range Across Layers')axes[1, 1].set_xlabel('Layer Index')axes[1, 1].set_ylabel('Weight Range')plt.tight_layout()plt.show()# 运行分析
pretrained_stats = analyze_pretrained_weights()
plot_weight_distributions(pretrained_stats)

不同层的权重特征

通过分析，我们发现预训练模型中不同类型层的权重具有不同特征：

1. 嵌入层：标准差通常在0.01-0.05之间
2. 注意力层：Q、K矩阵标准差较小，V矩阵标准差适中
3. 前馈网络：第一层（扩展）标准差较大，第二层（压缩）标准差较小
4. 输出层：标准差最小，通常在0.005-0.02之间

实际应用中的初始化最佳实践

通用初始化策略

基于理论分析和实验验证，我们可以总结出以下最佳实践：

class OptimalTransformerInit:"""优化的Transformer初始化策略"""@staticmethoddef init_model(model, config):"""统一的模型初始化入口"""for name, module in model.named_modules():if isinstance(module, nn.Linear):OptimalTransformerInit._init_linear(module, name, config)elif isinstance(module, nn.Embedding):OptimalTransformerInit._init_embedding(module, config)elif isinstance(module, nn.LayerNorm):OptimalTransformerInit._init_layernorm(module)@staticmethoddef _init_linear(module, name, config):"""线性层初始化"""d_model = config.d_modeln_layers = config.n_layers# 基础标准差base_std = config.get('init_std', 0.02)if 'attention' in name:if any(x in name for x in ['query', 'key']):# Q、K矩阵使用较小标准差std = base_std * 0.5elif 'value' in name:# V矩阵使用标准标准差std = base_stdelif 'out_proj' in name:# 输出投影使用深度缩放layer_id = OptimalTransformerInit._extract_layer_id(name)std = base_std / math.sqrt(2 * layer_id) if layer_id > 0 else base_stdelse:std = base_stdelif 'feed_forward' in name or 'mlp' in name:if 'fc1' in name or 'up_proj' in name:# 前馈网络第一层std = base_stdelif 'fc2' in name or 'down_proj' in name:# 前馈网络第二层，使用深度缩放layer_id = OptimalTransformerInit._extract_layer_id(name)std = base_std / math.sqrt(2 * layer_id) if layer_id > 0 else base_stdelse:std = base_stdelse:std = base_std# 应用初始化module.weight.data.normal_(mean=0.0, std=std)if module.bias is not None:module.bias.data.zero_()@staticmethoddef _init_embedding(module, config):"""嵌入层初始化"""std = config.get('embedding_init_std', 0.02)module.weight.data.normal_(mean=0.0, std=std)@staticmethoddef _init_layernorm(module):"""LayerNorm初始化"""module.weight.data.fill_(1.0)module.bias.data.zero_()@staticmethoddef _extract_layer_id(name):"""从层名称中提取层ID"""import rematch = re.search(r'layer\.(\d+)', name)return int(match.group(1)) + 1 if match else 0

自适应初始化策略

对于不同大小的模型，我们可以采用自适应的初始化策略：

class AdaptiveInit:"""自适应初始化策略"""@staticmethoddef compute_optimal_std(d_model, n_layers, layer_type='linear'):"""计算最优初始化标准差"""base_std = 0.02# 根据模型大小调整size_factor = min(1.0, math.sqrt(512 / d_model))# 根据深度调整depth_factor = min(1.0, math.sqrt(6 / n_layers))return base_std * size_factor * depth_factor@staticmethoddef init_with_fan_scaling(module, mode='fan_in'):"""使用扇入/扇出缩放的初始化"""if mode == 'fan_in':fan = module.weight.size(1)elif mode == 'fan_out':fan = module.weight.size(0)else:  # fan_avgfan = (module.weight.size(0) + module.weight.size(1)) / 2std = math.sqrt(2.0 / fan)module.weight.data.normal_(0, std)

训练稳定性监控

在训练过程中，我们需要监控初始化效果：

class InitializationMonitor:"""初始化效果监控"""def __init__(self, model):self.model = modelself.layer_stats = {}def record_stats(self, step):"""记录当前步骤的统计信息"""stats = {}for name, param in self.model.named_parameters():if param.grad is not None:stats[name] = {'weight_norm': param.data.norm().item(),'grad_norm': param.grad.norm().item(),'grad_to_weight_ratio': (param.grad.norm() / param.data.norm()).item()}self.layer_stats[step] = statsdef detect_issues(self):"""检测训练问题"""issues = []if not self.layer_stats:return issueslatest_stats = self.layer_stats[max(self.layer_stats.keys())]for name, stats in latest_stats.items():# 检测梯度爆炸if stats['grad_norm'] > 10.0:issues.append(f"Gradient explosion in {name}: {stats['grad_norm']:.2f}")# 检测梯度消失if stats['grad_norm'] < 1e-6:issues.append(f"Gradient vanishing in {name}: {stats['grad_norm']:.2e}")# 检测学习率过高if stats['grad_to_weight_ratio'] > 0.1:issues.append(f"High gradient-to-weight ratio in {name}: {stats['grad_to_weight_ratio']:.3f}")return issuesdef plot_training_dynamics(self):"""可视化训练动态"""if len(self.layer_stats) < 2:returnsteps = sorted(self.layer_stats.keys())layer_names = list(self.layer_stats[steps[0]].keys())fig, axes = plt.subplots(2, 2, figsize=(15, 10))# 权重范数变化for name in layer_names[:5]:  # 只显示前5层weight_norms = [self.layer_stats[step][name]['weight_norm'] for step in steps]axes[0, 0].plot(steps, weight_norms, label=name[:20])axes[0, 0].set_title('Weight Norms')axes[0, 0].legend()# 梯度范数变化for name in layer_names[:5]:grad_norms = [self.layer_stats[step][name]['grad_norm'] for step in steps]axes[0, 1].plot(steps, grad_norms, label=name[:20])axes[0, 1].set_title('Gradient Norms')axes[0, 1].legend()axes[0, 1].set_yscale('log')# 梯度/权重比值for name in layer_names[:5]:ratios = [self.layer_stats[step][name]['grad_to_weight_ratio'] for step in steps]axes[1, 0].plot(steps, ratios, label=name[:20])axes[1, 0].set_title('Gradient-to-Weight Ratios')axes[1, 0].legend()plt.tight_layout()plt.show()

深度解析：初始化的数学本质

信息论视角下的初始化

从信息论的角度来看，权重初始化实际上是在网络中注入适量的"信息熵"。如果初始化方差过小，网络缺乏足够的随机性来探索参数空间；如果方差过大，则信号被噪声淹没。

最优的初始化应该满足：
$$H(W)=-\sum p(w_i)\log p(w_i)$$

其中$H(W)$是权重的信息熵，$p(w_i)$是权重$w_i$的概率密度。

动力学系统视角

将神经网络训练视为动力学系统，权重初始化确定了系统的初始状态。优秀的初始化应该：

1. 避免不动点：权重不能初始化在损失函数的鞍点附近
2. 保证可达性：从初始状态出发，应该能够到达全局最优解
3. 稳定性：小的初始化扰动不应导致训练轨迹的剧烈变化

流形学习视角

在高维参数空间中，有效的参数构成一个低维流形。初始化的目标是将参数放置在这个流形的合适位置：

def analyze_parameter_manifold(model, num_samples=1000):"""分析参数流形结构"""from sklearn.decomposition import PCAfrom sklearn.manifold import TSNE# 收集不同初始化的参数parameter_samples = []for _ in range(num_samples):# 重新初始化模型init_model = type(model)(**model.config)OptimalTransformerInit.init_model(init_model, model.config)# 将参数展平params = torch.cat([p.flatten() for p in init_model.parameters()])parameter_samples.append(params.detach().numpy())parameter_samples = np.array(parameter_samples)# PCA分析pca = PCA(n_components=50)pca_result = pca.fit_transform(parameter_samples)# t-SNE可视化tsne = TSNE(n_components=2, random_state=42)tsne_result = tsne.fit_transform(pca_result)plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)plt.plot(pca.explained_variance_ratio_[:20], 'o-')plt.title('PCA Explained Variance Ratio')plt.xlabel('Principal Component')plt.ylabel('Explained Variance Ratio')plt.subplot(1, 2, 2)plt.scatter(tsne_result[:, 0], tsne_result[:, 1], alpha=0.6)plt.title('Parameter Space Visualization (t-SNE)')plt.xlabel('t-SNE Dimension 1')plt.ylabel('t-SNE Dimension 2')plt.tight_layout()plt.show()return pca_result, tsne_result

未来发展方向

神经架构搜索在初始化中的应用

随着神经架构搜索（NAS）技术的发展，我们可以自动搜索最优的初始化策略：

class InitializationNAS:"""初始化策略的神经架构搜索"""def __init__(self, search_space):self.search_space = search_spaceself.performance_history = []def search_optimal_init(self, model_factory, train_loader, val_loader, budget=100):"""搜索最优初始化策略"""best_score = float('-inf')best_strategy = Nonefor trial in range(budget):# 采样初始化策略strategy = self.sample_strategy()# 创建模型并应用策略model = model_factory()self.apply_strategy(model, strategy)# 快速训练评估score = self.quick_evaluation(model, train_loader, val_loader)if score > best_score:best_score = scorebest_strategy = strategyself.performance_history.append((strategy, score))return best_strategy, best_scoredef sample_strategy(self):"""从搜索空间采样初始化策略"""strategy = {}for param_name, options in self.search_space.items():strategy[param_name] = np.random.choice(options)return strategydef apply_strategy(self, model, strategy):"""应用初始化策略到模型"""for name, module in model.named_modules():if isinstance(module, nn.Linear):std = strategy.get('std_base', 0.02)if 'attention' in name:std *= strategy.get('attention_scale', 1.0)elif 'feed_forward' in name:std *= strategy.get('ff_scale', 1.0)module.weight.data.normal_(0, std)

元学习与初始化

元学习可以帮助我们学习如何为新任务选择合适的初始化：

class MetaInitializer:"""基于元学习的初始化器"""def __init__(self, meta_model):self.meta_model = meta_modeldef predict_optimal_init(self, task_features):"""根据任务特征预测最优初始化"""with torch.no_grad():init_params = self.meta_model(task_features)return init_paramsdef adapt_to_task(self, model, task_data):"""根据任务数据自适应调整初始化"""# 分析任务特征task_features = self.analyze_task(task_data)# 预测初始化参数init_params = self.predict_optimal_init(task_features)# 应用初始化self.apply_init(model, init_params)def analyze_task(self, task_data):"""分析任务特征"""# 这里可以包括数据分布、任务类型等特征pass

总结与思考

权重初始化虽然看似简单，实际上是深度学习成功的基石之一。通过本文的深入分析，我们可以得出以下关键洞察：

核心原则

1. 方差保持：好的初始化应该保持信号在前向和反向传播中的方差稳定
2. 对称性破坏：必须引入足够的随机性来打破神经元间的对称性
3. 深度适应：深层网络需要特殊的深度感知初始化策略
4. 层特异性：不同类型的层需要不同的初始化策略

实践建议

1. 从简单开始：对于新架构，先尝试标准的Xavier或He初始化
2. 逐步优化：根据训练表现逐步调整初始化策略
3. 监控训练：密切关注梯度流动和激活分布
4. 预训练优势：尽可能使用预训练权重作为起点

未来展望

随着模型规模的不断增大和架构的持续创新，初始化策略也需要不断演进。未来的发展方向可能包括：

1. 自适应初始化：根据模型架构和任务特点自动选择初始化策略
2. 动态初始化：在训练过程中动态调整参数初始化
3. 生物启发：借鉴神经科学中的发现来设计新的初始化方法

记住，权重初始化是一门艺术，也是一门科学。理论指导实践，但最终还需要通过实验来验证和优化。在探索大语言模型的征途中，每一个看似微小的技术细节都可能产生深远的影响。

通过掌握权重初始化的精髓，我们不仅能够训练出更稳定、更高效的模型，更能够深入理解深度学习的本质规律。这种理解将帮助我们在面对未来挑战时，做出更明智的技术选择。