深度学习①【张量、全连接神经网络、激活函数、交叉熵损失函数】

---

先言

深度学习（Deep Learning）作为人工智能的核心技术，正在重塑计算机视觉、自然语言处理、语音识别等领域。神经网络作为深度学习的基石，其强大的特征学习能力使其成为复杂任务的首选模型。

本文将带你系统了解深度学习的核心概念：
✅ PyTorch张量（Tensor）：深度学习的数据基石（基于自动微分）
✅ 全连接神经网络：一种最基本的神经网络结构
✅ 激活函数：神经网络的非线性灵魂（Sigmoid、tanh、ReLU、Softmax）
✅ 损失函数：交叉熵损失函数（CrossEntropyLoss）

无论你是刚入门的新手，还是希望巩固基础的开发者，这篇文章都将为你提供清晰的脉络和实用的代码示例！

---

前置要求：Pytorch安装

深度学习是基于pytorch环境下的模型学习，网络结构的模型运算需要用到其中的一种数据类型Tensor（张量）所以在进行下面学习的需要在自己的Python环境下安装Pytorch：参考文章Pytorch安装详解这里博主安装的cpu版本的，版本根据自己要求下载

一、张量（Tensor）

1.张量的基本概念

张量是一个多维数组，通俗来说可以看作是扩展了标量、向量、矩阵的更高维度的数组。张量的维度决定了它的形状（Shape），例如：

• 标量 是 0 维张量，如 a = torch.tensor(5)
• 向量 是 1 维张量，如 b = torch.tensor([1, 2, 3])
• 矩阵 是 2 维张量，如 c = torch.tensor([[1, 2], [3, 4]])
• 更高维度的张量，如3维、4维等，通常用于表示图像、视频数据等复杂结构。

2.张量的应用特点

• 动态计算图：PyTorch 支持动态计算图，这意味着在每一次前向传播时，计算图是即时创建的。
• GPU 支持：PyTorch 张量可以通过 .to('cuda') 移动到 GPU 上进行加速计算。
• 自动微分：通过 autograd 模块，PyTorch 可以自动计算张量运算的梯度，这对深度学习中的反向传播算法非常重要。

3.张量的数据类型

PyTorch中有3种数据类型：浮点数、整数、布尔。其中，浮点数和整数又分为8位、16位、32位、64位，加起来共9种。

• 为什么要分为8位、16位、32位、64位呢？

• 场景不同，对数据的精度和速度要求不同。通常，移动或嵌入式设备追求速度，对精度要求相对低一些。精度越高，往往效果也越好，自然硬件开销就比较高。

4.张量的创建方式

4.1基本创建方式

注意：这里的tensor是小写的

import torch
import numpy as np
def test001():# 1. 用标量创建张量tensor = torch.tensor(5)print(tensor.shape)# 2. 使用numpy随机一个数组创建张量tensor = torch.tensor(np.random.randn(3, 5))print(tensor)print(tensor.shape)# 3. 根据list创建tensortensor = torch.tensor([[1, 2, 3], [4, 5, 6]])print(tensor)print(tensor.shape)print(tensor.dtype)if __name__ == '__main__':test001()

4.2创建线性张量

使用torch.arange 和 torch.linspace 创建线性张量：

import torch
import numpy as np
# 不用科学计数法打印
torch.set_printoptions(sci_mode=False)
def test004():# 1. 创建线性张量r1 = torch.arange(0, 10, 2)print(r1)# 2. 在指定空间按照元素个数生成张量：等差r2 = torch.linspace(3, 10, 10)print(r2)r2 = torch.linspace(3, 10000000, 10)print(r2)if __name__ == "__main__":test004()

4.3创建随机张量

在 PyTorch 中，种子影响所有与随机性相关的操作，包括张量的随机初始化、数据的随机打乱、模型的参数初始化等。通过设置随机数种子，可以做到模型训练和实验结果在不同的运行中进行复现。

import torchdef test001():# 1. 设置随机数种子torch.manual_seed(123)# 2. 获取随机数种子，需要查看种子时调用print(torch.initial_seed())# 3. 生成随机张量，均匀分布（范围 [0, 1)）# 创建2个样本，每个样本3个特征print(torch.rand(2, 3))# 4. 生成随机张量：标准正态分布（均值 0，标准差 1）print(torch.randn(2, 3))# 5. 原生服从正态分布：均值为2， 方差为3，形状为1*4的正态分布print(torch.normal(mean=2, std=3, size=(1, 4)))if __name__ == "__main__":test001()

5.张量的函数梯度计算（自动微分）

在 PyTorch 中，当张量的 requires_grad=True 时，PyTorch 会自动跟踪与该张量相关的所有操作，并构建计算图。每个操作都会生成一个新的张量，并记录其依赖关系。当设置为 True 时，表示该张量在计算图中需要参与梯度计算，即在反向传播（Backpropagation）过程中会自动计算其梯度；当设置为 False 时，不会计算梯度。

例如：
$$\begin{gathered} z=x\ast y \\ loss=z.sum() \end{gathered}$$
在上述公式中，x 和 y 是输入张量，即叶子节点，z 是中间结果，loss 是最终输出。每一步操作都会记录依赖关系：
z = x * y：z 依赖于 x 和 y。
loss = z.sum()：loss 依赖于 z。

使用tensor.backward()方法执行反向传播，从而计算张量的梯度。这个过程会自动计算每个张量对损失函数的梯度。例如：调用 loss.backward() 从输出节点 loss 开始，沿着计算图反向传播，计算每个节点的梯度。

import torchdef test002():# 1. 创建张量：必须为浮点类型x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)# 2. 操作张量y = x ** 2# 3. 损失函数loss = y.mean()# 4. 计算梯度，也就是反向传播loss.backward()# 5. 读取梯度值print(x.grad)if __name__ == "__main__":test002()

和机器学习中的梯度下降对比下来pytorch具备自动微分的强大功能，使得编程过程更加简化

二、神经网络（全连接神经网络）

我们要学习的深度学习(Deep Learning)是神经网络的一个子领域，主要关注更深层次的神经网络结构，也就是深层神经网络（Deep Neural Networks，DNNs）。所以，我们需要先搞清楚什么是神经网络！

1.神经网络是什么？

神经网络（Neural Networks）是一种模拟人脑神经元网络结构的计算模型，用于处理复杂的模式识别、分类和预测等任务。生物神经元如下图：

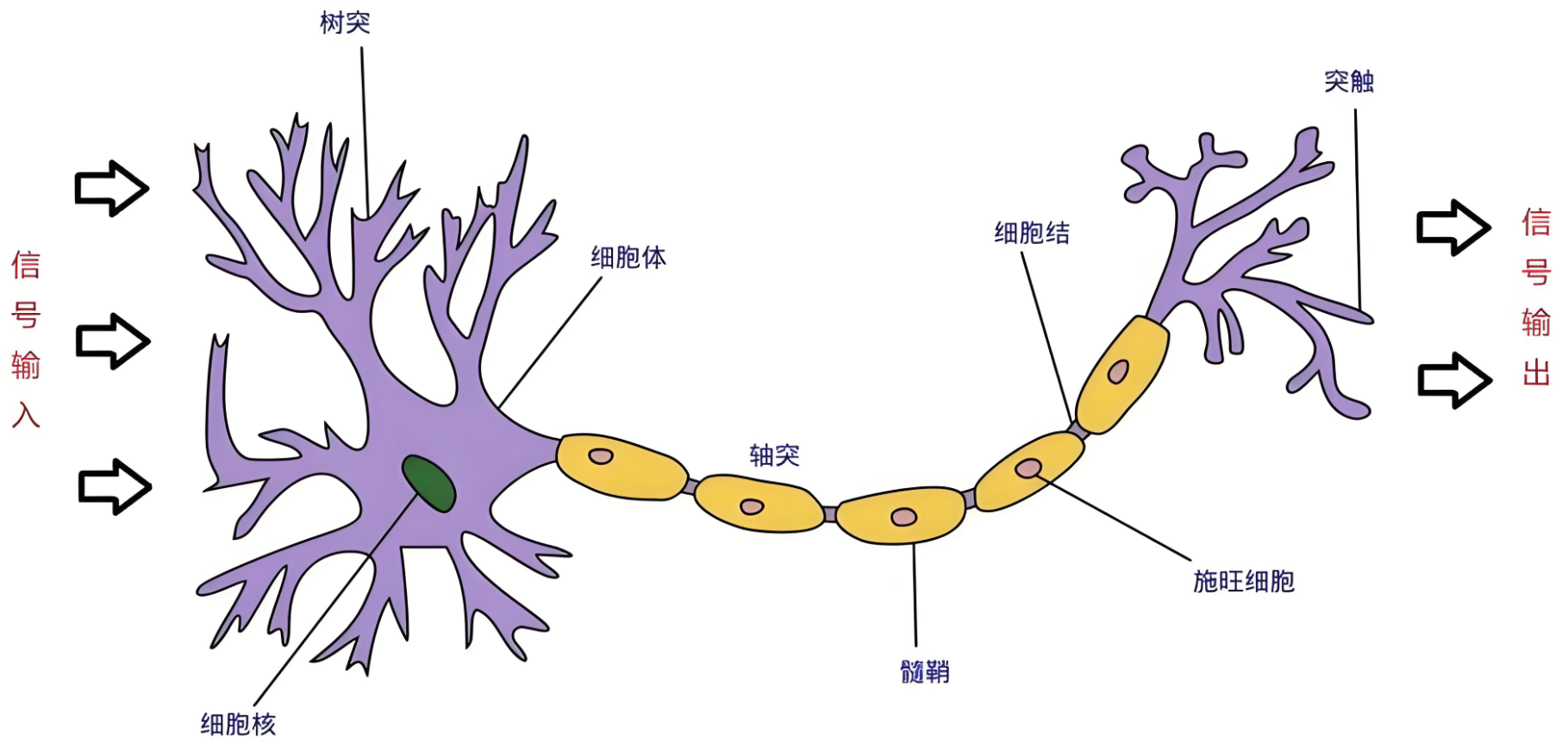
人脑可以看做是一个生物神经网络，由众多的神经元连接而成

• 树突：从其他神经元接收信息的分支
• 细胞核：处理从树突接收到的信息
• 轴突：被神经元用来传递信息的生物电缆
• 突触：轴突和其他神经元树突之间的连接

人脑神经元处理信息的过程：

• 多个信号到达树突，然后整合到细胞体的细胞核中
• 当积累的信号超过某个阈值，细胞就会被激活
• 产生一个输出信号，由轴突传递。

神经网络由多个互相连接的节点（即人工神经元）组成。

2.人工神经元：生物神经元启发的人工计算模型

人工神经元(Artificial Neuron)是神经网络的基本构建单元，模仿了生物神经元的工作原理。其核心功能是接收输入信号，经过加权求和和非线性激活函数处理后，输出结果。

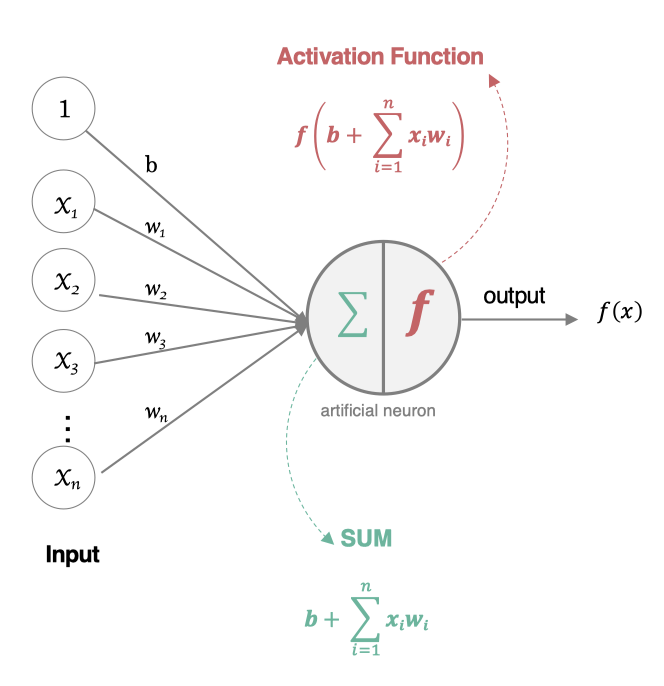
这里用到的数学公式：
$$\begin{gathered} z=\sum _{i=1}^n{w}_i\cdot x_i+b \\ y=\sigma (z) \end{gathered}$$
在往期文章机器学习系列文章中和和上面的公式差不多都是对所获取的数据进行加权求和得到一个预测值，所以机器学习为我们的深度学习打下了一定的基础，不过和之前的也有一些差别：
$\sigma (z)$是对所得到的结果进行非线性转换，也就是激活函数
有了激活函数的加成就引入一个算法概念：逻辑回归（在前面的机器就该讲的但写在这里方便全连接讲解）。

3.全连接神经网络（从结构到基本组件的搭建）

全连接神经网络（Fully Connected Neural Network，FCNN）是前馈神经网络的一种，每一层的神经元与上一层的所有神经元全连接，常用于图像分类、文本分类等任务。

3.1基本网络结构

神经网络有下面三个基础层（Layer）构建而成：

• 输入层（Input）: 神经网络的第一层，负责接收外部数据，不进行计算。

• 隐藏层（Hidden）: 位于输入层和输出层之间，进行特征提取和转换。隐藏层一般有多层，每一层有多个神经元。

• 输出层（Output）: 网络的最后一层，产生最终的预测结果或分类结果

3.2网络模型

我们使用多个神经元来构建神经网络，相邻层之间的神经元相互连接，并给每一个连接分配一个权重，经典如下：

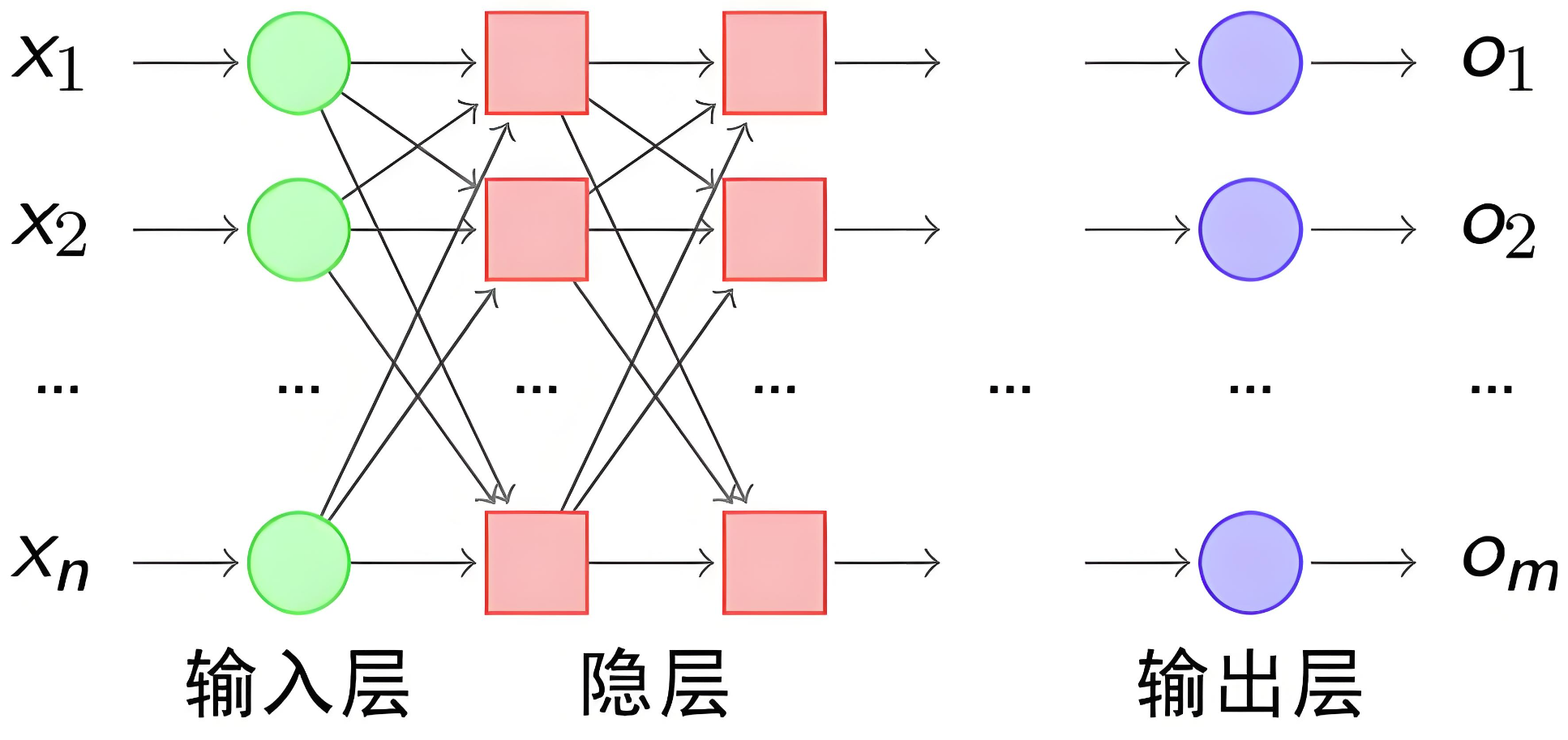
3.3全连接网络逻辑结构

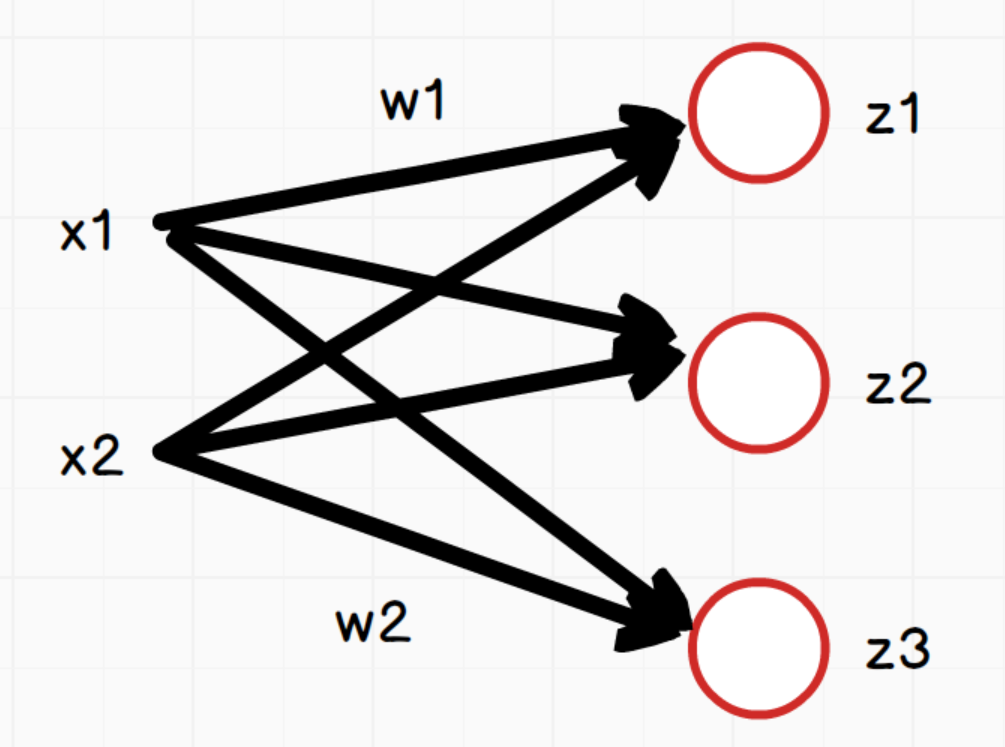
如上图，网络中每个神经元：
$$\begin{gathered} z_1=x_1\ast w_1+x_2\ast w_2+b_1 \\ {z}_2=x_1\ast w_1+x_2\ast w_2+b_2 \\ {z}_3=x_1\ast w_1+x_2\ast w_2+b_3 \end{gathered}$$
说明：三个等式中的w1和w2在这里只是为了方便表示对应x1和x2的权重，实际三个等式中的w值是不同的。

向量x为：$[x_1,x_2]$

向量w：$$\left(\begin{array}{c}{w}_1,w_2\\ w_1,w_2\\ w_1,w_2\end{array}\right)$$，其形状为（3，2），3是神经元节点个数，2是向量x的个数

向量z：$$[z_1,z_2,z_3]$$

向量b：$[b_1,b_2,b_3]$

所以用向量表示为：
$$z=\left(\begin{array}{c}{z}_1,z_2,z_3\end{array}\right)=\left(\begin{array}{c}{x}_1,x_2\end{array}\right)\left(\begin{array}{c}{w}_1,w_1,w_1\\ w_2,w_2,w_2\end{array}\right)+\left(\begin{array}{c}{b}_1,b_2,b_3\end{array}\right)=\left(\begin{array}{c}{x}_1,x_2\end{array}\right){\left(\begin{array}{c}{w}_1,w_2\\ w_1,w_2\\ w_1,w_2\end{array}\right)}^T+\left(\begin{array}{c}{b}_1,b_2,b_3\end{array}\right)=x{w}^T+b$$

• x是输入数据，形状为 (batch_size, in_features)。
• W是权重矩阵，形状为 (out_features, in_features)。
• b是偏置项，形状为 (out_features,)。
• z是输出数据，形状为 (batch_size, out_features)。

3.4 特点

• 全连接层: 层与层之间的每个神经元都与前一层的所有神经元相连。
• 权重数量: 由于全连接的特点，权重数量较大，容易导致计算量大、模型复杂度高。
• 学习能力: 能够学习输入数据的全局特征，但对于高维数据却不擅长捕捉局部特征（如图像就需要CNN）。

3.5 计算步骤

1. 数据传递: 输入数据经过每一层的计算，逐层传递到输出层。
2. 激活函数: 每一层的输出通过激活函数处理。
3. 损失计算: 在输出层计算预测值与真实值之间的差距，即损失函数值。
4. 反向传播（Back Propagation）: 通过反向传播算法计算损失函数对每个权重的梯度，并更新权重以最小化损失。

3.6.全连接神经网络线性层组件

nn.Linear是 PyTorch 中的一个非常重要的模块，用于实现全连接层（也称为线性层）。它是神经网络中常用的一种层类型，主要用于将输入数据通过线性变换映射到输出空间。

torch.nn.Linear(in_features, out_features, bias=True)

参数说明：

in_features：

• 输入特征的数量（即输入数据的维度）。
• 例如，如果输入是一个长度为 100 的向量，则 in_features=100。

out_features：

• 输出特征的数量（即输出数据的维度）。
• 例如，如果希望输出是一个长度为 50 的向量，则 out_features=50。

bias：

• 是否使用偏置项（默认值为 True）。
• 如果设置为 False，则不会学习偏置项。

示例：构建3层全连接神经网络：在__init__方法中定义网络结构，在forward定义前向传播
代码示例：

import torch
from torch import nn
#多层神经网络
class Net(nn.Module):def __init__(self,in_features,out_features):super().__init__()self.fc1 = nn.Linear(in_features, 10)self.fc2 = nn.Linear(10, 1)self.fc3 = nn.Linear(10, out_features)def forward(self, x):x = self.fc1(x)x = self.fc2(x)x = self.fc3(x)return x
model = Net(2,1)
print(model)
#单层神经网络
model1 = nn.Linear(2,1)
print(model1)
#顺序容器：Sequential
model= nn.Sequential(nn.Linear(2,10),nn.Linear(10,1)
)
print(model)

以上是创建线性层网络结构的三种方式
在创建神经网络模型的时候一般是以类的方式创建
接下来我们使用单层神经网络搭建基础全连接网络模型，这里以鸢尾花数据为例：

import torch
import torch.nn as nn
from sklearn.datasets import load_iris
iris = load_iris()
x = torch.tensor(iris.data[:5],dtype=torch.float32)
y = torch.tensor(iris.target[:5],dtype=torch.float32)
def MSE(x,y):model = nn.Linear(4,1)#创建单层神经网络模型loss = nn.MSELoss()#构建损失函数opt = torch.optim.SGD(model.parameters(),lr=0.001) #构建优化器和学习率for epoch in range(10):y_pred = model(x)#前向传播模型预测loss_value = loss(y_pred,y).sum() #计算损失opt.zero_grad() #梯度清零loss_value.backward() #反向传播opt.step() #更新参数w = model.weight#权重参数b = model.bias #偏置参数print(f'第{epoch+1}次更新损失为：{loss_value.item()}，权重参数为：{w.tolist()}，偏置参数为：{b.item()}')
MSE(x,y)

三、激活函数

激活函数的作用是在隐藏层引入非线性，使得神经网络能够学习和表示复杂的函数关系，使网络具备非线性能力，增强其表达能力。

1.第一个激活函数sigmoid

激活函数的值是在[0,1]区间中的一个概率值,默认为0.5为阈值可以自己设定,大于0.5认为是正例,小于则认为是负例
sigmoid激活函数：
$$f(x)=\frac{1}{1+e^{-x}}$$
函数图像：

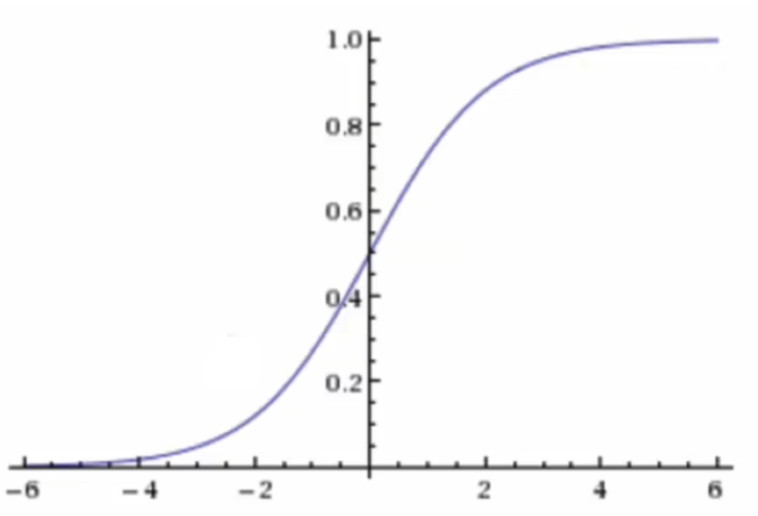
通过线性回归计算的输出再输入到激活函数中就可以实现分类：

经过链式求导，根据损失函数得到最佳参数，但是有一个致命缺点，我们在进行链式求导时，sigmoid作为最外层函数求导时会面临梯度消失等问题，我们通过上面的sigmoid的函数图可以进一步求出外层函数梯度的范围并画出导函数图如下：

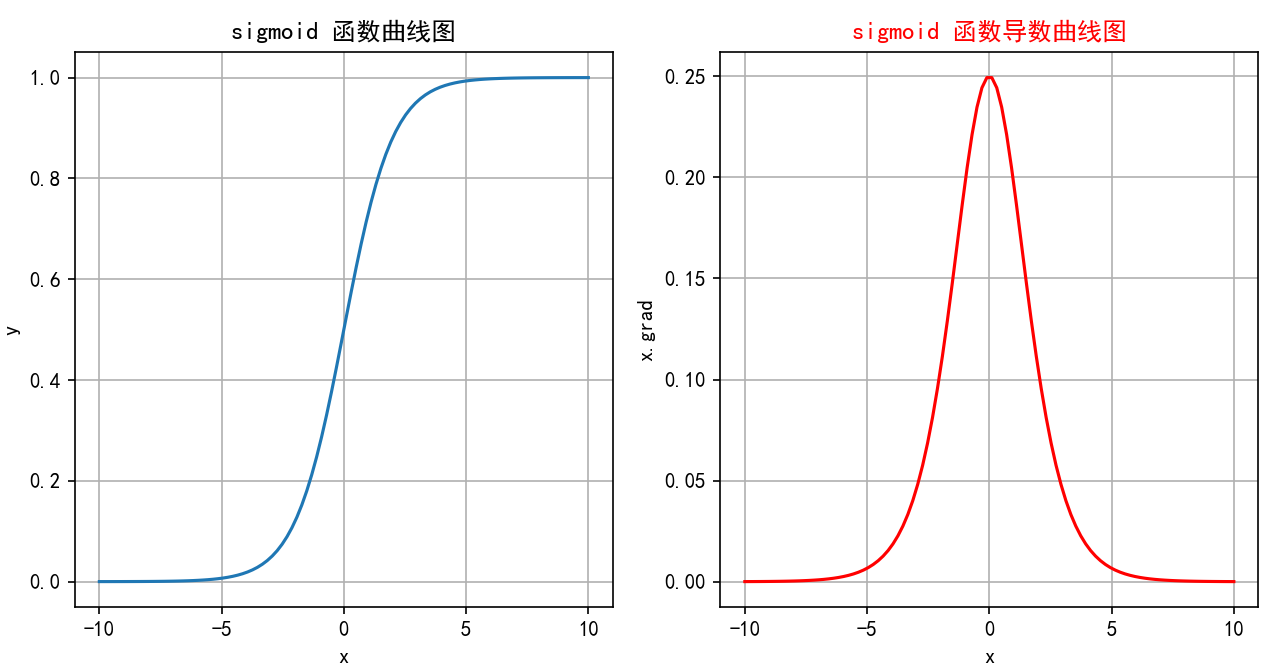
在全连接神经网络进行反向传播使梯度下降，sigmoid函数的导函数每一次都在参与计算，通过导函数的数值分布，很容易面临梯度乘零问题导致梯度下降逐渐衰减，最终使得早期层的权重更新非常缓慢，进而导致训练速度变慢甚至停滞。
所以sigmoid函数一般只用于二分类的输出层。

2.tanh(双曲正切)

tanh(双曲正切)是一种常见的非线性激活函数，常用于神经网络的隐藏层。tanh 函数也是一种S形曲线，输出范围也为$(-1,1)$。

tanh数学表达式为：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
tanh的函数图像：

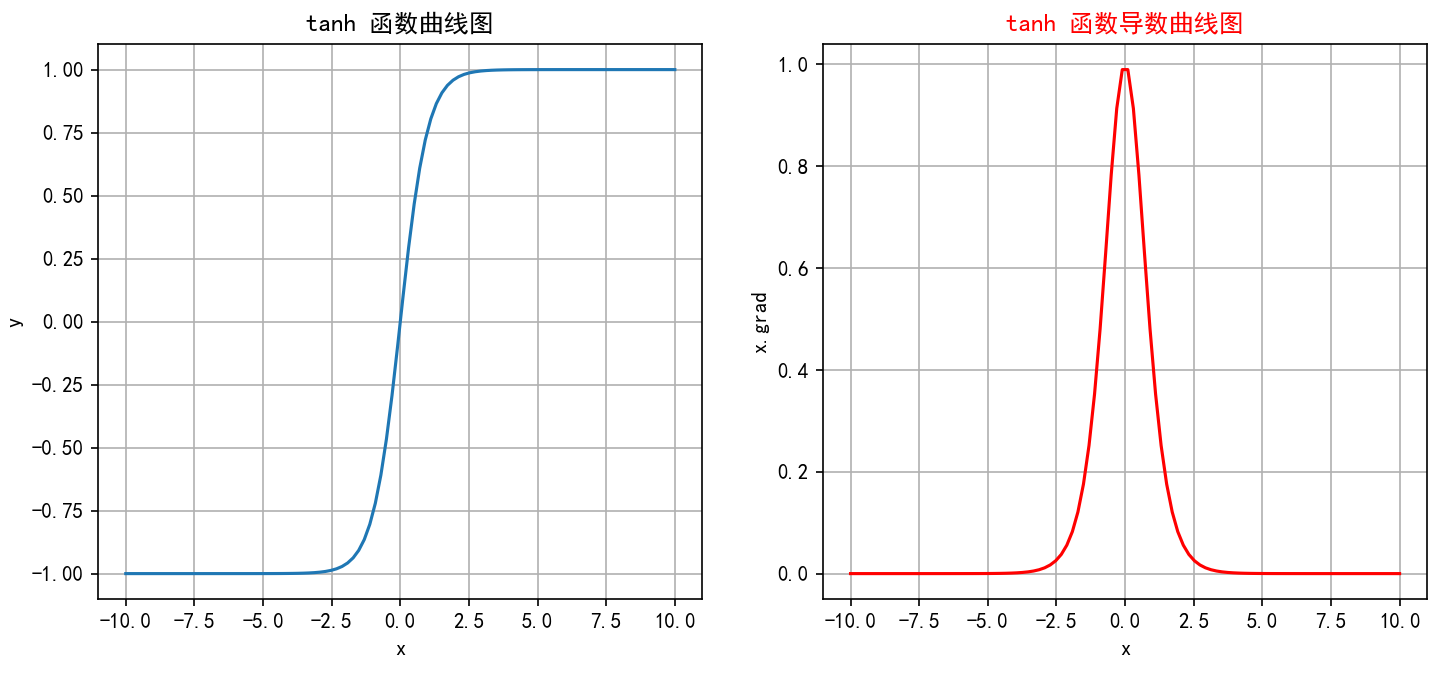
对比sigmoid函数，tanh函数是一个奇函数且取值范围在（-1，1）之间，这有利于对全连接网络的数据平衡，又观察tanh函数的导函数图像可知，tanh导函数的取值范围在（0，1）之间相比于sigmoid提高了四倍，一定程度上减少了梯度衰减与消失的概率。

不仅如此，anh函数在整个输入范围内都是连续且可微的，这使其非常适合于使用梯度下降法进行优化。
$$\frac{d}{dx}\text{tanh}(x)=1-{\text{tanh}}^2(x)$$
但tanh依旧存在以下缺点：

1. 虽然一定程度上改善了梯度消失问题，但在输入值非常大或非常小时导数还是非常小，这在深层网络中仍然是个问题。这是因为每一层的梯度都会乘以一个小于1的值，经过多层乘积后，梯度会变得非常小，导致训练过程变得非常缓慢，甚至无法收敛。
2. 由于涉及指数运算，Tanh的计算成本还是略高，尽管差异不大。

3.ReLU修正线性单元（Rectified Linear Unit）

ReLU（Rectified Linear Unit）是深度学习中最常用的激活函数之一，它的全称是修正线性单元。ReLU 激活函数的定义非常简单，但在实践中效果非常好。

ReLU 函数定义如下：
$$\text{ReLU}(x)=\max (0,x)$$
ReLU函数图像：

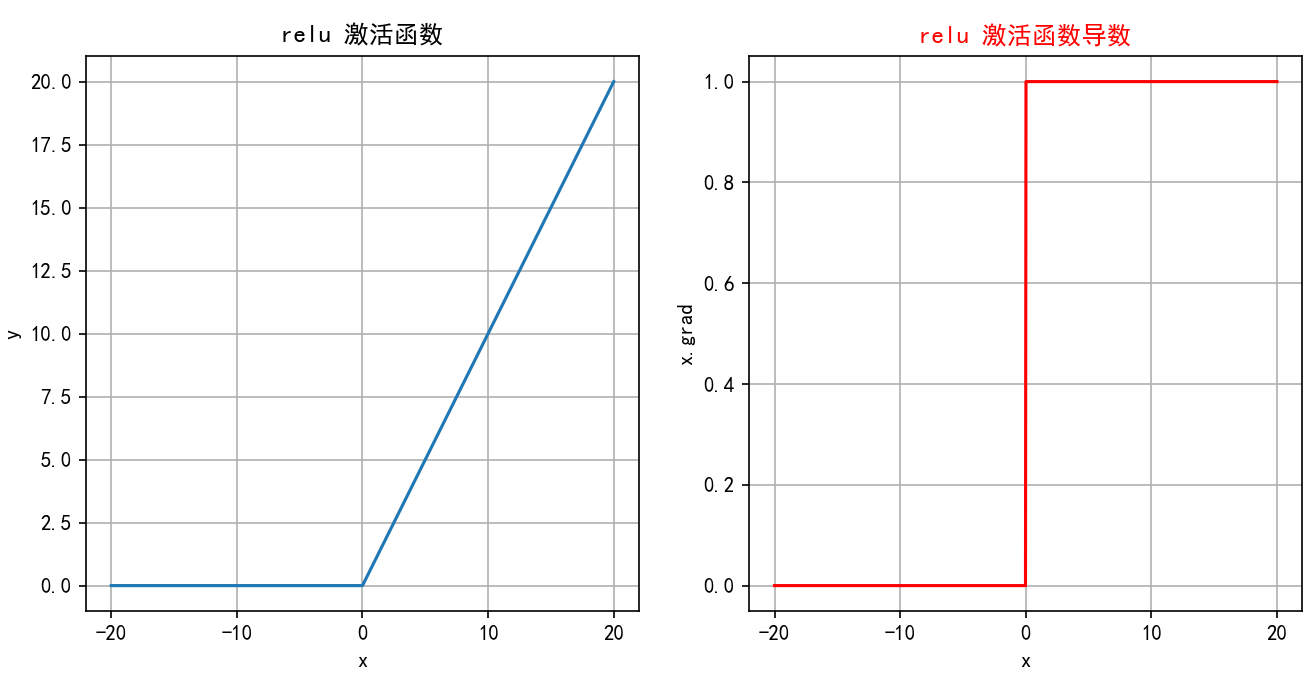
$ReLU$对输入$x$进行非线性变换：
$$\begin{gathered} \bullet \text{当 }x>0\text{ 时,ReLU}(x)=x \\ \bullet \text{当 }x\le 0\text{ 时,ReLU}(x)=0 \end{gathered}$$

ReLU函数包括以下特点：

1. 计算简单：ReLU 的计算非常简单，只需要对输入进行一次比较运算，这在实际应用中大大加速了神经网络的训练。

2. ReLU 函数的导数是分段函数：
   $${\text{ReLU}}^{\prime }(x)=\{\begin{array}{ll}1,& \text{if }x>0\\ 0,& \text{if }x\le 0\end{array}$$

3. 缓解梯度消失问题：相比于 Sigmoid 和 Tanh 激活函数，ReLU 在正半区的导数恒为 1，这使得深度神经网络在训练过程中可以更好地传播梯度，不存在饱和问题。

4. 稀疏激活：ReLU在输入小于等于 0 时输出为 0，这使得 ReLU 可以在神经网络中引入稀疏性（即一些神经元不被激活），这种稀疏性可以减少网络中的冗余信息，提高网络的效率和泛化能力。

神经元死亡：由于$ReLU$在$x\le 0$时输出为$0$，如果某个神经元输入值是负，那么该神经元将永远不再激活，成为“死亡”神经元。随着训练的进行，网络中可能会出现大量死亡神经元，从而会降低模型的表达能力。
因为上述缺点，开发这对ReLU函数进行了优化和升级，所以Leaky ReLU 函数出现了，对比ReLU它有了一点浅浅的变化，函数公式如下：

$$\text{Leaky ReLU}(x)=\{\begin{array}{ll}x,& \text{if }x>0\\ \alpha x,& \text{if }x\le 0\end{array}$$

其中，$\alpha$ 是一个非常小的常数（如 0.01），它控制负半轴的斜率。这个常数 $\alpha$是一个超参数，可以在训练过程中可自行进行调整。

Leaky ReLU函数有以下特点：

1. 避免神经元死亡：通过在$x\le 0$ 区域引入一个小的负斜率，这样即使输入值小于等于零，Leaky ReLU仍然会有梯度，允许神经元继续更新权重，避免神经元在训练过程中完全“死亡”的问题。
2. 计算简单：Leaky ReLU 的计算与 ReLU 相似，只需简单的比较和线性运算，计算开销低。
3. 美中不足：如果$\alpha$ 设定得不当，仍然可能导致激活值过低。

4.softmax

Softmax激活函数通常用于分类问题的输出层，它能够将网络的输出转换为概率分布，使得输出的各个类别的概率之和为 1。Softmax 特别适合用于多分类问题。

公式
假设神经网络的输出层有$n$个节点，每个节点的输入为$z_i$，则 Softmax 函数的定义如下：
$$\mathrm{Softmax}(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$

给定输入向量 $z=[z_1,z_2,\dots ,z_n]$

1.指数变换：对每个 $z_i$进行指数变换，得到 $t=[e^{z_1},e^{z_2},...,e^{z_n}]$，使z的取值区间从$(-\infty ,+\infty )$变为$(0,+\infty )$

2.将所有指数变换后的值求和，得到$s=e^{z_1}+e^{z_2}+...+e^{z_n}={\Sigma }_{j=1}^n{e}^{z_j}$

3.将t中每个 $e^{z_i}$除以归一化因子s，得到概率分布:
$$softmax(z)=[\frac{e^{z_1}}{s},\frac{e^{z_2}}{s},...,\frac{e^{z_n}}{s}]=[\frac{e^{z_1}}{{\Sigma }_{j=1}^n{e}^{z_j}},\frac{e^{z_2}}{{\Sigma }_{j=1}^n{e}^{z_j}},...,\frac{e^{z_n}}{{\Sigma }_{j=1}^n{e}^{z_j}}]$$
即：
$$\mathrm{Softmax}(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$
从上述公式可以看出：

1. 每个输出值在 (0,1)之间

2. Softmax()对向量的值做了改变，但其位置不变

3. 所有输出值之和为1，即

$$sum(softmax(z))=\frac{e^{z_1}}{s}+\frac{e^{z_2}}{s}+...+\frac{e^{z_n}}{s}=\frac{s}{s}=1$$

softmax特点：

1. 将输出转化为概率：通过$Softmax$，可以将网络的原始输出转化为各个类别的概率，从而可以根据这些概率进行分类决策。

2. 概率分布：$Softmax$的输出是一个概率分布，即每个输出值$$\text{Softmax}(z_i)$$都是一个介于$0$和$1$之间的数，并且所有输出值的和为 1：
   $$\sum _{i=1}^n\text{Softmax}(z_i)=1$$

3. 突出差异：$Softmax$会放大差异，使得概率最大的类别的输出值更接近$1$，而其他类别更接近$0$。

4. 在实际应用中，$Softmax$常与交叉熵损失函数Cross-Entropy Loss结合使用，用于多分类问题。在反向传播中，$Softmax$的导数计算是必需的。

$$\begin{array}{rlrl}& \text{设 }{p}_i=\mathrm{Softmax}(z_i)\text{,则对于 }{z}_i\text{ 的导数为:}& & \\ & \bullet \text{ 当 }i=j\text{ 时:}& & \\ & & & \frac{\partial p_i}{\partial z_i}=\frac{e^{z_i}({\Sigma }_{j=1}^n{e}^{z_j})-e^{z_i}{e}^{z_i}}{({\Sigma }_{j=1}^n{e}^{z_j}{)}^2}=p_i(1-p_i)\\ & \bullet \text{ 当 }i\ne j\text{ 时}:& & \\ & & & \frac{\partial p_i}{\partial z_j}=\frac{0({\Sigma }_{j=1}^n{e}^{z_j})-e^{z_i}{e}^{z_j}}{({\Sigma }_{j=1}^n{e}^{z_j}{)}^2}=-p_i{p}_j\end{array}$$

四、交叉熵损失函数

在往期机器学习文章决策树算法中有所讲到过信息熵的概念，交叉熵是在信息熵的基础上，通过计算信息量期望得到信息熵，再通过KL散度实现交叉熵的求解：

其中KL散度用于衡量两个概率分布之间的差异。它描述的是用一个分布 Q来近似另一个分布 P时，所损失的信息量。KL散度越小，表示两个分布越接近。

对于两个离散概率分布 P和 Q，KL散度定义为：
$$D_{KL}(P||Q)=\sum _{i}P(x_i)log\frac{P(x_i)}{Q(x_i)}$$
其中：P 是真实分布，Q是近似分布。
对KL散度公式展开：
$$\begin{gathered} D_{KL}(P||Q)=\sum _{i}P(x_i)log\frac{P(x_i)}{Q(x_i)}=\sum _{i}P(x_i)[logP(x_i)-logQ(x_i)] \\ =\sum _{i}P(x_i)logP(x_i)-\sum _{i}P(x_i)logQ(x_i)=-(-\sum _{i}P(x_i)logP(x_i))+(-\sum _{i}P(x_i)logQ(x_i)) \\ =-H(P)+(-\sum _{i}P(x_i)logQ(x_i)) \\ =H(P,Q)-H(P) \end{gathered}$$
由上述公式可知，P是真实分布，H§是常数，所以KL散度可以用H(P,Q)来表示；H(P,Q)叫做交叉熵。

如果将P换成y，Q换成$\hat{y}$,则交叉熵公式为：
$$\text{CrossEntropyLoss}(y,\hat{y})=-\sum _{i=1}^C{y}_i\log ({\hat{y}}_i)$$

其中：

• $C$ 是类别的总数。
• $y$ 是真实标签的one-hot编码向量，表示真实类别。
• $\hat{y}$ 是模型的输出（经过 softmax 后的概率分布）。
• $y_i$ 是真实类别的第 $i$ 个元素（0 或 1）。
• ${\hat{y}}_i$ 是预测的类别概率分布中对应类别 $i$ 的概率。

重点：

通过交叉熵函数信息中的$y_i$是one-hot编码，其值不是1便是0，又是乘法，所以只要知道1对应的index就可以了，展开后：
$$\text{Loss}(y,\hat{y})=-\log ({\hat{y}}_m)$$
其中，m表示真实类别。

因为神经网络最后一层分类总是接softmax，所以可以把${\hat{y}}_m$直接看为是softmax后的结果。
$$\text{Loss}(i)=-\log (softmax(x_i))$$
所以，CrossEntropyLoss 实质上是两步的组合：Cross Entropy = Log-Softmax + NLLLoss，意味着交叉熵函数是自带softmax激活函数的，所以一般在输出层不需要额外在设置激活函数，否则会造成数据干扰和梯度衰减。
代码示例（敲一敲）：

import torch
from torch import nn
#多元交叉熵损失函数内置softmax函数
def test():#还没有处理过的输出层值x = torch.tensor([[1.0,2.0],[3.0,4.0]])y = torch.tensor([1,2])criterion = nn.CrossEntropyLoss()loss = criterion(x,y)print(loss)
test()def test02():x = torch.tensor([[1.0],[2.0],[3.0],[4.0]])y = torch.tensor([[0],[1],[0],[1]])#整合sigmoid激活函数的二元交叉熵损失函数criterion = nn.BCEWithLogitsLoss()

---

结语

神经网络是深度学习的核心框架，理解其基本原理和实现细节是迈向AI工程师的第一步。本文从理论到实践，为你搭建了系统化的学习路径。

🚀 动手尝试：文中的代码示例已提供，快打开Colab运行吧！你对哪种神经网络最感兴趣？欢迎在评论区留言讨论！

📌 下篇预告：《全连接神经网络——梯度下降优化、数据获取到全连接网络模型训练及应用的进化之路》