K-Means 聚类算法详解与实战指南

在机器学习的世界里，聚类算法就像一位 “自动分类大师”，能在没有标签的情况下将相似数据聚为一类。其中，K-Means 算法以其简单高效的特点成为最常用的聚类方法之一。本文将从基础概念到代码实战，全方位带你掌握 K-Means 算法的核心原理与应用技巧。

一、聚类算法：无监督学习的 “分类魔法”

聚类算法属于无监督学习的范畴，它解决的核心问题是：如何在没有标签的情况下，将相似的数据自动分为若干组。

二、距离度量：量化数据相似性的工具

距离度量是聚类的基础，常用的两种距离度量方式如下：

1. 欧式距离（Euclidean Distance）

最常见的距离度量方式，衡量多维空间中两点的直线距离：

1.欧式距离          

欧式距离也称欧几里得距离，是最常见的距离度量，衡量的是多维空间中两个点之间的绝对距离 。        

 在二维和三维空间中的欧式距离的就是两点之间的距离。 ·

二维空间里的欧氏距离公式：           ·

三维空间里的欧氏距离公式：           ·

n 维空间里的欧氏距离公式：

2. 曼哈顿距离（Manhattan Distance）

也叫 “出租车距离”，计算两点在坐标系上的绝对轴距总和：

平面上两点(x1​,y1​)与(x2​,y2​)的距离：d(i,j)=|X1-X2|+|Y1-Y2|

小贴士：欧式距离适合衡量 “直线距离”，曼哈顿距离适合在网格状空间（如城市道路）中使用。

三、K-Means 算法：简单高效的聚类核心

K-Means 算法的核心思想是：通过迭代找到 k 个聚类中心，使数据点到所属中心的距离之和最小。

算法步骤（核心流程）

初始化：随机选择 k 个样本作为初始聚类中心

样本聚类：计算每个样本到各中心的距离，将样本分配到最近的中心所属类别

更新中心：计算每个类别中所有样本的均值，作为新的聚类中心

迭代收敛：重复步骤 2 和 3，直到聚类中心不再变化或达到最大迭代次数

算法流程图解

四、聚类效果评估：CH 指标

如何判断聚类结果的好坏？CH 指标（Calinski-Harabasz Index） 是常用的评估指标：

类内紧密度：计算类中各点与类中心的距离平方和

类间分离度：计算各类中心点与数据集总中心的距离平方和

评估标准：CH 值越大，说明类内越紧密、类间越分散，聚类效果越好

五、K-Means 的优缺点分析

优点

原理简单，易于理解和实现

计算效率高，适合处理大规模数据集

对高维数据有一定的适应性

缺点

k 值需要手动指定：需通过经验或评估指标确定最优 k 值

对初始聚类中心敏感：不同初始中心可能导致不同结果

难以发现非凸形状的簇：对复杂分布的数据聚类效果较差

复杂度与样本量呈线性关系：极端大规模数据可能需要优化

六、实战：用 Scikit-learn 实现 K-Means 聚类

下面我们通过代码实战，使用 Scikit-learn 库实现 K-Means 聚类。

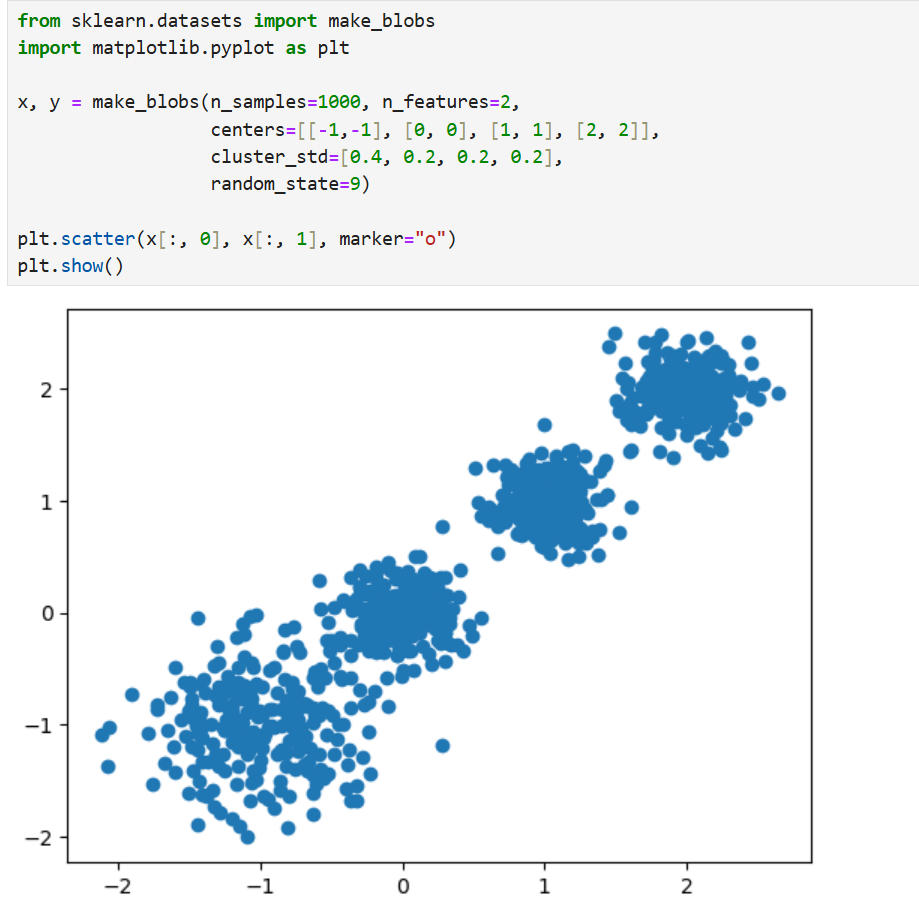
使用make_blobs()函数生成聚类专用数据集：

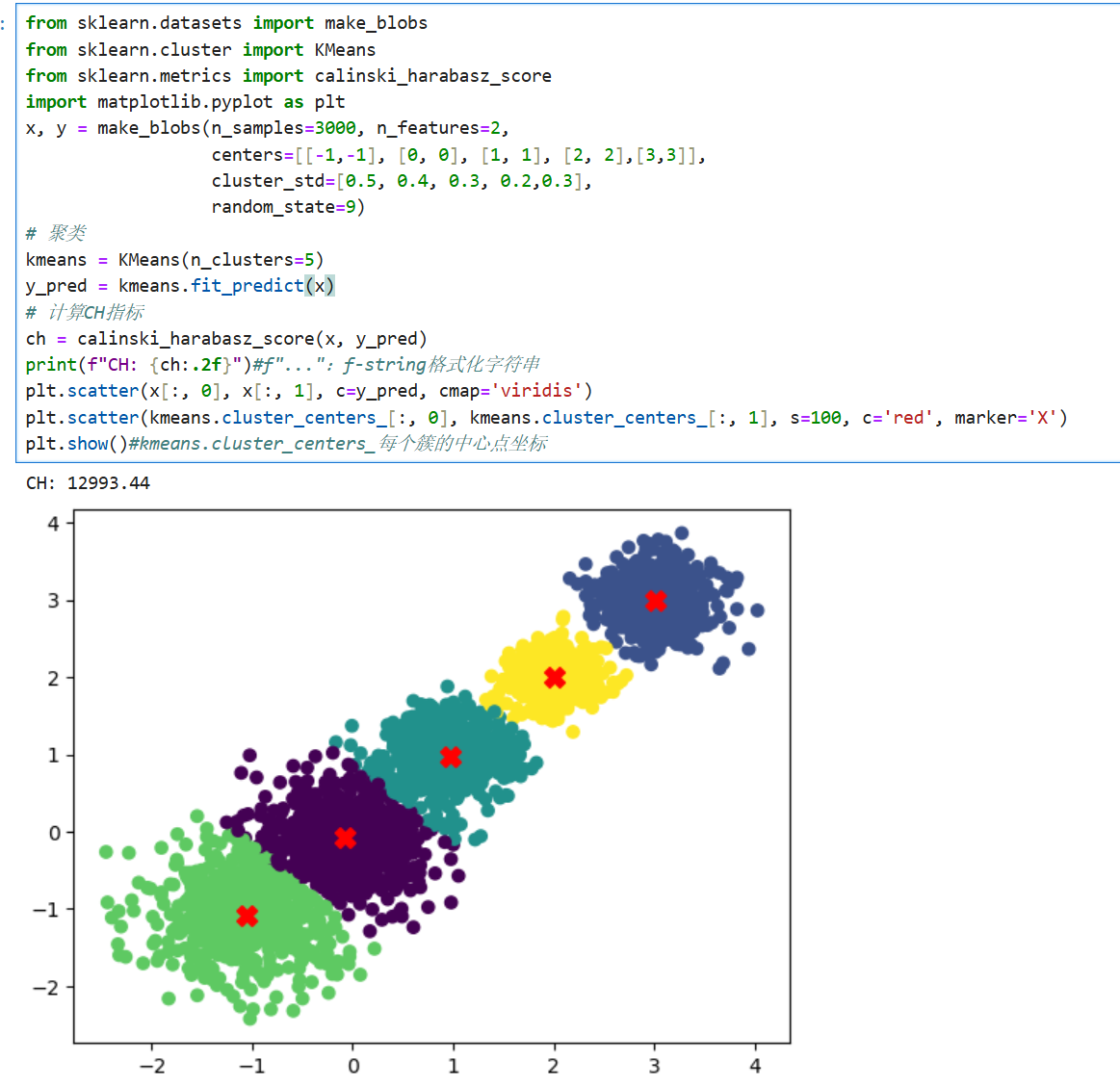
计算CH指标

七、总结与拓展

K-Means 作为经典的聚类算法，以其简单高效的特点在数据分析、图像分割、用户分群等领域广泛应用。但在实际使用中需注意：

提前通过可视化或评估指标确定合适的 k 值

可尝试多次初始化以避免局部最优解

对于高维数据，可先通过 PCA 降维再聚类

希望本文能帮助你快速掌握 K-Means 算法的核心知识。