数据结构 二叉树 二叉树链式结构的实现

1. 二叉树链式结构的实现

1.1 前置说明

核心目标：
通过手动构建简单二叉树的示例，快速进入二叉树操作学习阶段，后续再深入研究动态创建逻辑。

关键代码解析：

typedef int BTDataType; 
typedef struct BinaryTreeNode {BTDataType _data;          // 存储节点数据（如整数）struct BinaryTreeNode* _left;  // 指向左子树struct BinaryTreeNode* _right; // 指向右子树
} BTNode; 

• BTNode 结构体：用 _data 存值，_left/_right 指针维护二叉树的递归结构。
• 递归定义体现：二叉树 = 根节点 + 左子树（二叉树） + 右子树（二叉树），为空则指针为 NULL。

手动创建二叉树示例：

BTNode* BuyNode(BTDataType x) {BTNode* newNode = (BTNode*)malloc(sizeof(BTNode));newNode->_data = x;newNode->_left = NULL;newNode->_right = NULL;return newNode;
}BTNode* CreatBinaryTree() {BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;  // 根节点1的左孩子是2node1->_right = node4; // 根节点1的右孩子是4node2->_left = node3;  // 节点2的左孩子是3node4->_left = node5;  // 节点4的左孩子是5node4->_right = node6; // 节点4的右孩子是6return node1; // 返回根节点，代表整棵树
}

• 构建的二叉树结构（简化示意）：

         1/  \2    4/    / \3    5   6
  

• 注意：这是硬编码式创建，仅用于快速学习操作；真实场景需动态构建（如从数组、字符串、文件解析 ），后续会详细讲解。

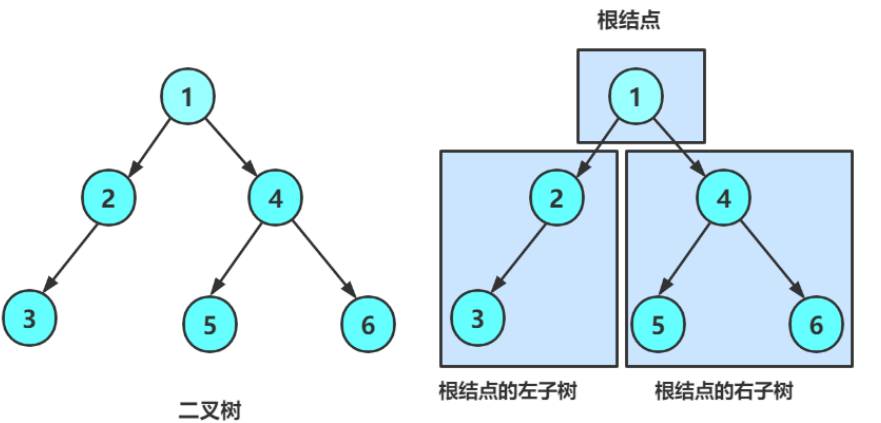
二叉树的递归定义回顾：
二叉树是以下两种情况之一：

1. 空树：root = NULL。
2. 非空树：由根节点、左子树（也是二叉树）、右子树（也是二叉树） 组成。

该定义是后续实现遍历、高度、节点数统计等操作的核心依据（递归思想的典型应用 ）

1.2 二叉树的遍历

1.2.1 前序、中序以及后序遍历

遍历核心定义：
二叉树遍历是按特定规则（前序/中序/后序）依次访问每个节点，且每个节点仅访问一次。核心依据二叉树的递归定义（根+左子树+右子树），差异仅在于“访问根节点的时机”。

遍历规则与符号约定：

• 用 N 表示“访问根节点”，L 表示“遍历左子树”，R 表示“遍历右子树”。
• 前序遍历：N→L→R（根先访问，再左、再右）。
• 中序遍历：L→N→R（左先遍历，再根、再右）。
• 后序遍历：L→R→N（左、右先遍历，最后根）。

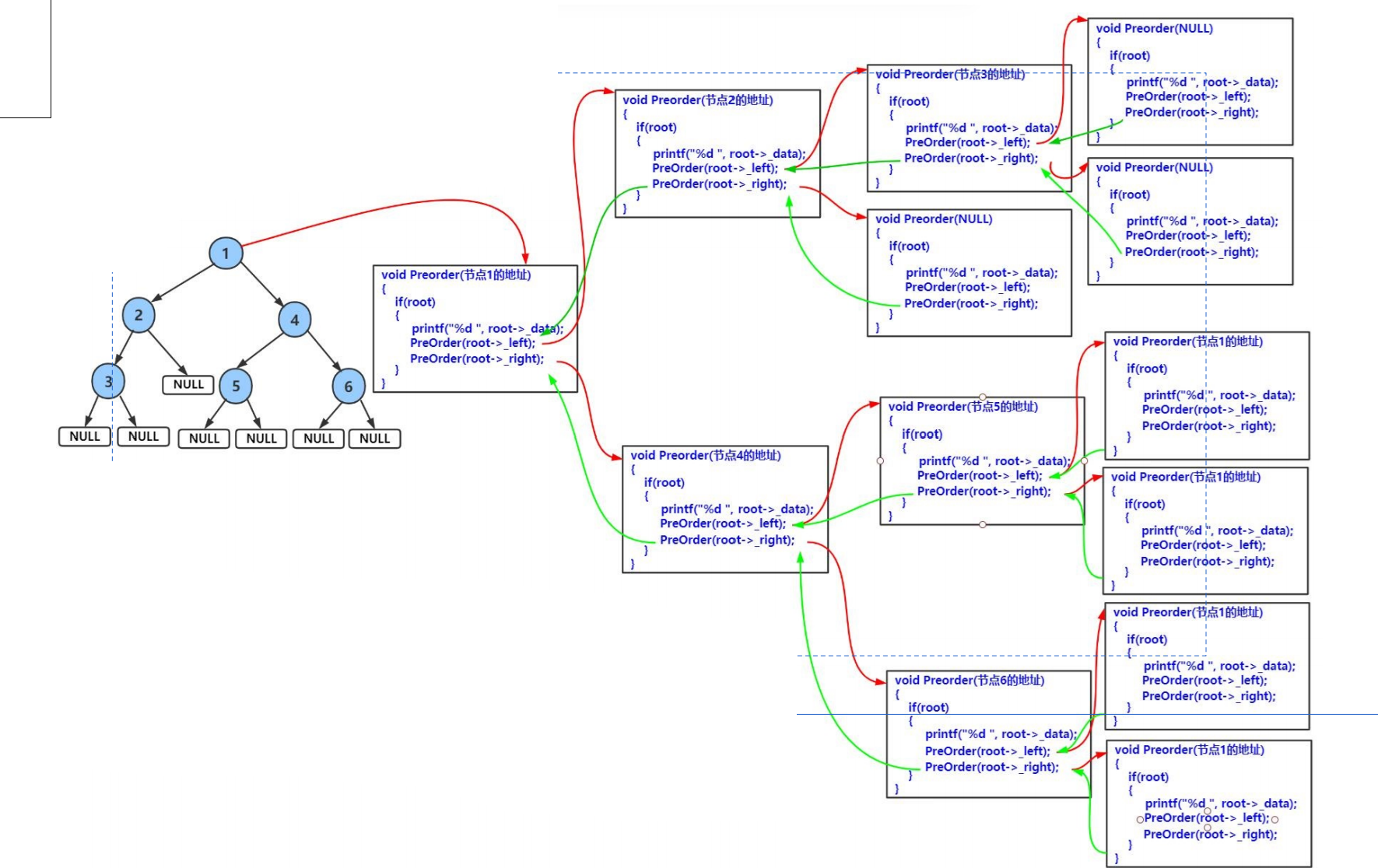
1. 前序遍历（Preorder Traversal，NLR）

规则：访问根节点 → 递归遍历左子树 → 递归遍历右子树。

结合示例树解析（示例树结构：根1，左子树2（左3、右空），右子树4（左5、右6））：

1. 访问根节点 1（N）→ 记录结果：1。
2. 递归遍历 1 的左子树（根2）：
   • 访问根节点 2（N）→ 记录结果：1 2。
   • 递归遍历 2 的左子树（根3）：
     • 访问根节点 3（N）→ 记录结果：1 2 3。
     • 3 的左、右子树均为空，递归返回。
   • 2 的右子树为空，递归返回。
3. 递归遍历 1 的右子树（根4）：
   • 访问根节点 4（N）→ 记录结果：1 2 3 4。
   • 递归遍历 4 的左子树（根5）：
     • 访问根节点 5（N）→ 记录结果：1 2 3 4 5。
     • 5 的左、右子树为空，返回。
   • 递归遍历 4 的右子树（根6）：
     • 访问根节点 6（N）→ 记录结果：1 2 3 4 5 6。
     • 6 的左、右子树为空，返回。

最终前序遍历结果：1 2 3 4 5 6（与给定结果一致）。

代码实现

// 二叉树前序遍历
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->_data);PrevOrder(root->_left);PrevOrder(root->_right);}

2. 中序遍历（Inorder Traversal，LNR）

规则：递归遍历左子树 → 访问根节点 → 递归遍历右子树。

结合示例树解析：

1. 递归遍历根 1 的左子树（根2）：
   • 递归遍历 2 的左子树（根3）：
     • 递归遍历 3 的左子树（空），返回。
     • 访问根节点 3（N）→ 记录结果：3。
     • 递归遍历 3 的右子树（空），返回。
   • 访问根节点 2（N）→ 记录结果：3 2。
   • 递归遍历 2 的右子树（空），返回。
2. 访问根节点 1（N）→ 记录结果：3 2 1。
3. 递归遍历根 1 的右子树（根4）：
   • 递归遍历 4 的左子树（根5）：
     • 递归遍历 5 的左子树（空），返回。
     • 访问根节点 5（N）→ 记录结果：3 2 1 5。
     • 递归遍历 5 的右子树（空），返回。
   • 访问根节点 4（N）→ 记录结果：3 2 1 5 4。
   • 递归遍历 4 的右子树（根6）：
     • 递归遍历 6 的左子树（空），返回。
     • 访问根节点 6（N）→ 记录结果：3 2 1 5 4 6。
     • 递归遍历 6 的右子树（空），返回。

最终中序遍历结果：3 2 1 5 4 6（与给定结果一致）。

代码实现

void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->_left);printf("%c ", root->_data);InOrder(root->_right);
}

3. 后序遍历（Postorder Traversal，LRN）

规则：递归遍历左子树 → 递归遍历右子树 → 访问根节点。

结合示例树解析：

1. 递归遍历根 1 的左子树（根2）：
   • 递归遍历 2 的左子树（根3）：
     • 递归遍历 3 的左子树（空），返回。
     • 递归遍历 3 的右子树（空），返回。
     • 访问根节点 3（N）→ 记录结果：3。
   • 递归遍历 2 的右子树（空），返回。
   • 访问根节点 2（N）→ 记录结果：3 2。
2. 递归遍历根 1 的右子树（根4）：
   • 递归遍历 4 的左子树（根5）：
     • 递归遍历 5 的左子树（空），返回。
     • 递归遍历 5 的右子树（空），返回。
     • 访问根节点 5（N）→ 记录结果：3 2 5。
   • 递归遍历 4 的右子树（根6）：
     • 递归遍历 6 的左子树（空），返回。
     • 递归遍历 6 的右子树（空），返回。
     • 访问根节点 6（N）→ 记录结果：3 2 5 6。
   • 访问根节点 4（N）→ 记录结果：3 2 5 6 4。
3. 访问根节点 1（N）→ 记录结果：3 2 5 6 4 1。

最终后序遍历结果：3 2 5 6 4 1（与给定结果一致）。

代码实现

// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->_left);PostOrder(root->_right);printf("%c ", root->_data);
}

4. 三种遍历的核心差异与联系

差异核心：仅“访问根节点的时机”不同，遍历左、右子树的顺序始终是“先左后右”。

联系：

• 均基于递归实现，依赖二叉树“根+左+右”的递归结构。
• 遍历左、右子树的逻辑完全复用，仅需调整“访问根节点”的代码位置。

示例结果对比：

遍历类型	访问顺序（N/L/R）	遍历结果
前序	N→L→R	1 2 3 4 5 6
中序	L→N→R	3 2 1 5 4 6
后序	L→R→N	3 2 5 6 4 1

关键结论：
已知“中序遍历结果”+“前序/后序遍历结果”，可唯一确定一棵二叉树（前序定根，中序分左右；后序定根，中序分左右），这是二叉树遍历的重要应用场景（如重构二叉树）。

1.2.2前序遍历递归图解：

1.3. 二叉树的层序遍历与核心属性计算

1.3.1 层序遍历

核心定义：
层序遍历是按“自上而下、自左至右”的层级顺序访问节点，即先访问第1层（根节点），再第2层所有节点，依次类推，每个节点仅访问一次。其本质是“广度优先搜索（BFS）”在二叉树中的应用，需依赖队列实现（先进先出特性适配层级顺序）。

实现逻辑（结合代码解析）：

void BinaryTreeLevelOrder(BTNode* root) {Queue q;QueueInit(&q);  // 初始化队列（存储节点指针，用于维护层级顺序）if (root == NULL)  // 空树直接返回，无需遍历return;QueuePush(&q, root);  // 根节点入队，作为第1层的起始// 队列非空时，循环处理当前层节点while (!QueueEmpty(&q)) {BTNode* Front = QueueFront(&q);  // 取队头节点（当前层待访问节点）QueuePop(&q);                    // 队头节点出队（已访问，后续处理其子节点）printf("%c ", Front->_data);     // 访问节点（此处为打印数据，可按需修改操作）// 左子节点非空则入队（保证下一层按左到右顺序）if (Front->_left)QueuePush(&q, Front->_left);// 右子节点非空则入队if (Front->_right)QueuePush(&q, Front->_right);}QueueDestory(&q);  // 遍历结束，销毁队列释放资源printf("\n");
}

示例解析（基于前文示例树：根 1，左 2（左 3），右 4（左 5、右 6））：

初始化队列，根节点 1 入队 → 队列：[1]。

• 第一次循环：
  取队头 1，出队 → 打印1；左 2、右 4 入队 → 队列：[2,4]（第 2 层节点）。
• 第二次循环：
  取队头 2，出队 → 打印2；左 3 入队、右空 → 队列：[4,3]。
• 第三次循环：
  取队头 4，出队 → 打印4；左 5、右 6 入队 → 队列：[3,5,6]（第 3 层节点）。
• 第四次循环：
  取队头 3，出队 → 打印3；左右空 → 队列：[5,6]。
• 第五次循环：
  取队头 5，出队 → 打印5；左右空 → 队列：[6]。
• 第六次循环：
  取队头 6，出队 → 打印6；左右空 → 队列空。
• 遍历结束，最终打印结果：1 2 4 3 5 6（符合层序顺序）。

关键依赖：
队列的 “先进先出” 特性确保了 “先处理当前层节点，再入队下一层节点”，严格遵循层级顺序；遍历后需销毁队列，避免内存泄漏。

1.4 节点个数及高度等核心属性计算

1.4.1 二叉树节点总数（TreeSize）

功能：统计二叉树中所有节点的总个数（包括根、分支节点、叶子节点）。

实现逻辑（递归思想）：

• 空树节点数为0；
• 非空树节点数 = 1（当前根节点） + 左子树节点数 + 右子树节点数（递归拆分左右子树）。

代码解析：

int TreeSize(BTNode* root) {if (root == NULL)  // 递归终止条件：空树无节点，返回0return 0;else  // 递归递推：当前节点计数1，加上左右子树的节点数return 1 + TreeSize(root->_left) + TreeSize(root->_right);
}

1.4.2 二叉树叶子节点个数（TreeLeafSize）

功能：统计二叉树中度为0的节点（叶子节点，无左、右子树）个数。

实现逻辑（递归思想）：

• 空树叶子数为0；
• 若当前节点无左、右子树（叶子节点），计数1；
• 非叶子节点的叶子数 = 左子树叶子数 + 右子树叶子数（递归拆分）。

代码解析：

int TreeLeafSize(BTNode* root) {if (root == NULL)  // 递归终止：空树无叶子，返回0return 0;// 递归终止：当前节点是叶子，返回1if (root->_left == NULL && root->_right == NULL)return 1;else  // 递推：非叶子节点，叶子数来自左右子树return TreeLeafSize(root->_left) + TreeLeafSize(root->_right);
}

示例验证（示例树）：

• 叶子节点为 3、5、6（共 3 个）；
• 计算过程：
  • TreeLeafSize (1) = TreeLeafSize (2) + TreeLeafSize (4)；
  • TreeLeafSize(2) = TreeLeafSize(3) + 0 = 1 + 0 = 1；
  • TreeLeafSize(4) = TreeLeafSize(5) + TreeLeafSize(6) = 1 + 1 = 2；
• 总叶子数：1 + 2 = 3（与实际一致）。

1.4.3 二叉树深度（TreeDepth）

功能：计算二叉树的高度（从根节点到最远叶子节点的最大层数，根节点为第1层）。

实现逻辑（递归思想）：

• 空树深度为0；
• 非空树深度 = max(左子树深度, 右子树深度) + 1（取左右子树较深的一层，加当前根节点的1层）。

代码解析：

int TreeDepth(BTNode* root) {if (root == NULL)  // 递归终止：空树深度0return 0;else  // 递推：取左右子树深度的最大值，加当前层return (TreeDepth(root->_left) > TreeDepth(root->_right) ? TreeDepth(root->_left) : TreeDepth(root->_right)) + 1;
}

示例验证（示例树）：

• 左子树（1-2-3）深度：TreeDepth (2) = TreeDepth (3) + 1 = 1 + 1 = 2；
• 右子树（1-4-5、1-4-6）深度：TreeDepth (4) = max (TreeDepth (5), TreeDepth (6)) + 1 = 1 + 1 = 2；
• 总深度：max (2, 2) + 1 = 3（根 1 为第 1 层，2/4 为第 2 层，3/5/6 为第 3 层，深度 3）。

1.4.4 二叉树第k层节点个数（BinaryTreeLevelkSize）

功能：统计二叉树第k层（根为第1层）的节点总数。

实现逻辑（递归思想）：

• 空树或k<1：第k层节点数0；
• k=1：当前节点即为第1层，计数1；
• k>1：第k层节点数 = 左子树第k-1层节点数 + 右子树第k-1层节点数（递归将“找第k层”转化为“找子树第k-1层”）。

代码解析：

int BinaryTreeLevelkSize(BTNode* root, int k) {if (root == NULL || k < 1)  // 终止：空树或k无效，返回0return 0;if (k == 1)  // 终止：k=1，当前节点是第1层，返回1return 1;// 递推：第k层节点来自左右子树的第k-1层return BinaryTreeLevelkSize(root->_left, k - 1) + BinaryTreeLevelkSize(root->_right, k - 1);
}

示例验证（示例树，k=3）：

• 找第 3 层节点数 → 转化为找左右子树（2、4）的第 2 层节点数；
  • 左子树 2 的第 2 层：BinaryTreeLevelkSize (2,2) = BinaryTreeLevelkSize (3,1) + 0 = 1；
  • 右子树 4 的第 2 层：BinaryTreeLevelkSize (4,2) = BinaryTreeLevelkSize (5,1) + BinaryTreeLevelkSize (6,1) = 1+1=2；
• 第 3 层总节点数：1 + 2 = 3（对应节点 3、5、6，与实际一致）。

1.4.5 二叉树查找值为x的节点（BinaryTreeFind）

功能：在二叉树中查找数据域为x的节点，找到返回节点指针，未找到返回NULL。

实现逻辑（递归思想）：

• 空树：返回NULL；
• 当前节点数据为x：返回当前节点指针；
• 未找到则递归查找左子树，找到返回左子树中的节点；
• 左子树未找到则递归查找右子树，找到返回右子树中的节点；
• 左右子树均未找到：返回NULL。

代码解析：

BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {if (root == NULL)  // 终止：空树无节点，返回NULLreturn NULL;if (root->_data == x)  // 终止：找到目标节点，返回指针return root;// 递推：先查左子树BTNode* node = BinaryTreeFind(root->_left, x);if (node)  // 左子树找到，直接返回return node;// 左子树未找到，查右子树node = BinaryTreeFind(root->_right, x);if (node)  // 右子树找到，返回return node;// 左右子树均未找到，返回NULLreturn NULL;
}

1.4.6 二叉树销毁（DestoryTree）

功能：释放二叉树所有节点的动态内存，避免内存泄漏（需后序遍历顺序，先销毁子节点再销毁根）。

实现逻辑（递归思想）：

• 空树：直接返回（无内存需释放）；
• 非空树：先递归销毁左子树，再递归销毁右子树，最后释放当前根节点（后序顺序，避免先销毁根导致子节点指针失效）。

代码解析：

void DestoryTree(BTNode* root) {if (root == NULL)  // 终止：空树无需销毁，返回return;// 递推：先销毁左、右子树DestoryTree(root->_left);DestoryTree(root->_right);free(root);  // 最后释放当前根节点// （可选）将root置NULL，避免野指针（需传入二级指针，当前代码无此操作，调用者需注意）
}

关键注意：
销毁后原根节点指针变为野指针，调用者需手动将其置 NULL（如 DestoryTree(&root); root = NULL;，若函数参数为一级指针则无法内部置空）。

1.4.7 判断二叉树是否为完全二叉树（BinaryTreeComplete）

功能：判断二叉树是否为完全二叉树（完全二叉树是“除最后一层外，每一层节点数满，最后一层节点靠左连续”的二叉树），是返回1，否返回0。

实现逻辑（基于层序遍历+队列）：

• 空树：是完全二叉树，返回1；
• 根节点入队，层序遍历所有节点；
• 遇到NULL节点则停止遍历，后续队列中若存在非NULL节点 → 不是完全二叉树（存在空缺）；
• 后续队列全为NULL → 是完全二叉树。

代码解析：

int BinaryTreeComplete(BTNode* root) {Queue q;QueueInit(&q);  // 初始化队列if (root == NULL)  // 空树是完全二叉树return 1;QueuePush(&q, root);  // 根节点入队// 层序遍历，遇到NULL则breakwhile (!QueueEmpty(&q)) {BTNode* Front = QueueFront(&q);QueuePop(&q);if (Front == NULL)  // 遇到NULL，停止遍历后续非NULL节点break;// 无论子节点是否为NULL，均入队（用于后续判断连续性）QueuePush(&q, Front->_left);QueuePush(&q, Front->_right);}// 检查后续队列是否全为NULLwhile (!QueueEmpty(&q)) {BTNode* Front = QueueFront(&q);QueuePop(&q);if (Front) {  // 存在非NULL节点 → 不是完全二叉树QueueDestory(&q);return 0;}}QueueDestory(&q);  // 销毁队列return 1;  // 后续全为NULL → 是完全二叉树
}

1.4.7 判断二叉树是否为完全二叉树（BinaryTreeComplete）

功能：判断二叉树是否为完全二叉树（完全二叉树是“除最后一层外，每一层节点数满，最后一层节点靠左连续”的二叉树），是返回1，否返回0。

实现逻辑（基于层序遍历+队列）：

• 空树：是完全二叉树，返回1；
• 根节点入队，层序遍历所有节点；
• 遇到NULL节点则停止遍历，后续队列中若存在非NULL节点 → 不是完全二叉树（存在空缺）；
• 后续队列全为NULL → 是完全二叉树。

代码解析：

int BinaryTreeComplete(BTNode* root) {Queue q;QueueInit(&q);  // 初始化队列if (root == NULL)  // 空树是完全二叉树return 1;QueuePush(&q, root);  // 根节点入队// 层序遍历，遇到NULL则breakwhile (!QueueEmpty(&q)) {BTNode* Front = QueueFront(&q);QueuePop(&q);if (Front == NULL)  // 遇到NULL，停止遍历后续非NULL节点break;// 无论子节点是否为NULL，均入队（用于后续判断连续性）QueuePush(&q, Front->_left);QueuePush(&q, Front->_right);}// 检查后续队列是否全为NULLwhile (!QueueEmpty(&q)) {BTNode* Front = QueueFront(&q);QueuePop(&q);if (Front) {  // 存在非NULL节点 → 不是完全二叉树QueueDestory(&q);return 0;}}QueueDestory(&q);  // 销毁队列return 1;  // 后续全为NULL → 是完全二叉树
}