当前位置：首页 > news >正文

【论文阅读】-《SIGN-OPT: A QUERY-EFFICIENT HARD-LABEL ADVERSARIAL ATTACK》

news 2025/8/21 9:34:16

Sign-OPT: 一种查询高效的硬标签对抗攻击

在这里插入图片描述
原文链接：https://arxiv.org/pdf/1909.10773

摘要

我们研究在访问受限情况下评估机器学习系统对抗鲁棒性的最实用问题设置：用于生成对抗样本的硬标签黑盒攻击设置，其中允许有限的模型查询，并且只向查询的数据输入提供决策（标签）。针对此问题已经提出了几种算法，但它们通常需要大量（>20,000）查询来攻击一个样本。其中，一种最先进的方法（Cheng et al., 2019）表明，硬标签攻击可以建模为一个优化问题，其目标函数可以通过额外的模型查询进行二分搜索来评估，从而可以应用零阶优化算法。在本文中，我们采用相同的优化公式，但提出直接估计任意方向上的梯度符号而不是梯度本身，这享有单次查询的好处。利用这种用于检索方向导数符号的单次查询预言机，我们开发了一种新颖的、查询高效的 Sign-OPT 方法用于硬标签黑盒攻击。我们提供了新算法的收敛性分析，并在 MNIST、CIFAR-10 和 ImageNet 上的多个模型上进行了实验。我们发现，与当前最先进的方法相比，Sign-OPT 攻击始终需要少 5 到 10 倍的查询次数，并且通常收敛到具有更小扰动的对抗样本。

1 引言

已经证明神经网络容易受到对抗样本的攻击（Szegedy et al., 2016; Goodfellow et al., 2015; Carlini & Wagner, 2017; Athalye et al., 2018）。给定一个受害神经网络模型和一个正确分类的样本，对抗攻击旨在计算一个小的扰动，使得添加此扰动后，原始样本将被误分类。文献中已经提出了许多对抗攻击。其中大多数考虑白盒设置，攻击者完全了解受害模型，因此可以使用基于梯度的优化进行攻击。流行的例子包括 C&W（Carlini & Wagner, 2017）和 PGD（Madry et al., 2017）攻击。另一方面，一些更近期的攻击考虑了概率黑盒设置，攻击者不知道受害模型的结构和权重，但可以迭代地查询模型并获得相应的概率输出。在此设置中，虽然（输出概率对输入层的）梯度无法计算，但仍可以使用有限差分进行估计，许多攻击算法都基于此（Chen et al., 2017; Ilyas et al., ; Tu et al., 2019; Jun et al., 2018）。

在本文中，我们考虑最具挑战性和实用性的攻击设置——硬标签黑盒设置——其中模型对攻击者是隐藏的，攻击者只能进行查询并获得模型相应的硬标签决策（例如，预测标签）。在此设置下提出的常用算法，也称为边界攻击（Brendel et al., 2017），基于决策边界上的随机游走，但它没有任何收敛保证。最近，Cheng et al. (2019) 表明，在硬标签设置中寻找最小对抗扰动可以重新表述为另一个优化问题（我们在本文中称之为 Cheng 公式）。这个新公式的优点是在大多数任务中具有平滑的边界，并且函数值可以使用硬标签查询计算。因此，（Cheng et al., 2019）的作者能够使用标准的零阶优化来解决新公式。尽管他们的算法收敛很快，但由于 Cheng 公式的每次函数评估都必须使用需要数十次查询的二分搜索来计算，因此攻击单个图像仍然需要大量查询（例如，20,000 次）。

在本文中，我们遵循（Cheng et al., 2019）相同的优化公式，该公式具有平滑性的优点，但我们不使用有限差分来估计方向导数的大小，而是提出仅使用单次查询来评估其符号。利用这种单次查询符号预言机，我们设计了新颖的算法来求解 Cheng 公式，并且我们从理论上证明并凭经验证明了硬标签黑盒攻击所需查询次数的显著减少。

我们的贡献总结如下：

*对抗攻击方面的新颖性。 我们阐明了一种使用单次查询计算 Cheng 公式方向导数符号的有效方法，并基于此技术开发了一种名为 Sign-OPT 的新颖优化算法用于硬标签黑盒攻击。
*优化方面的新颖性。 我们的方法可以看作是一种新的零阶优化算法，具有 signSGD 的快速收敛特性。我们的算法不是直接获取梯度估计的符号，而是利用了随机方向的尺度。这使得现有分析不适用于我们的情况，我们提供了一种新的方法来证明这种新优化器的收敛性。
*我们在多个数据集和模型上进行了全面的实验。我们表明，所提出的算法在不同模型和数据集上始终将查询次数减少 5-10 倍，表明这是一种实用且查询高效的鲁棒性评估工具。此外，在大多数数据集上，与以前的方法相比，我们的算法可以找到具有更小失真的对抗样本。

2 相关工作

白盒攻击 自从首次发现神经网络容易被对抗样本欺骗（Goodfellow et al., 2015）以来，在白盒攻击设置下已经提出了大量工作，其中分类器 $f$ 完全暴露给攻击者。对于神经网络，在此假设下，可以在目标模型上进行反向传播，因为攻击者知道网络结构和权重。基于梯度计算的算法包括（Goodfellow et al., 2015; Kurakin et al., 2016; Carlini & Wagner, 2017; Chen et al., 2018; Madry et al., 2017）。最近，Athalye et al. (2018) 引入的 BPDA 攻击绕过了一些具有混淆梯度的模型，并被证明可以成功规避许多防御。除了基于小 $ℓp\ell_{p}$ 范数扰动的典型攻击外，还考虑了非 $ℓp\ell_{p}$ 范数扰动，例如缩放或平移（Zhang et al., 2019）。

黑盒攻击 最近，黑盒设置正迅速引起越来越多的关注。在黑盒设置中，攻击者可以查询模型，但无法（直接）访问模型内部的任何信息。尽管有一些基于迁移攻击的工作（Papernot et al., 2017），但我们在本文中考虑基于查询的攻击。根据模型对给定查询的反馈，攻击可分为软标签攻击或硬标签攻击。在软标签设置中，模型为每个决策输出概率分数。Chen et al. (2017) 使用坐标方式的有限差分来近似估计输出概率变化，并进行坐标下降来执行攻击。Ilyas et al. () 使用神经进化策略（NES）来直接近似估计梯度。随后，提出了一些变体（Ilyas et al., ; Tu et al., 2019）来利用辅助信息进一步加速攻击过程。Alzantot et al. (2019) 使用进化算法作为软标签设置的黑盒优化器。最近，Al-Dujaili & O’Reilly (2019) 提出了基于 signSGD（Bernstein et al., 2018）的 SignHunter 算法，以在软标签设置中实现更快的收敛。最近的工作（Al-Dujaili & O’Reilly, 2019）提出了 SignHunter 算法，在通过软标签信息制作黑盒对抗样本时，实现更查询高效的符号估计。
在硬标签情况下，只观察到最终决策，即 top-1 预测类别。因此，攻击者只能进行查询以获取相应的硬标签决策，而不是概率输出。Brendel et al. (2017) 首先研究了这个问题，并提出了一种基于
决策边界附近随机游走的算法。通过在每次迭代中选择一个随机方向并将其投影到一个边界球面上，它旨在生成高质量的对抗样本。查询有限攻击（Ilyas et al., 2018a）尝试通过模型查询估计输出概率分数，并将硬标签问题转化为软标签问题。Cheng et al. (2019) 则重新将硬标签攻击形式化为一个优化问题，即找到一个能产生到决策边界最短距离的方向。最近的 arXiv 论文（Chen et al., 2019）应用零阶符号预言机来改进边界攻击，并也展示了显著改进。与我们算法的主要区别在于我们提出了一种新的零阶梯度下降算法，提供了其算法收敛性保证，并旨在改进（Cheng et al., 2019）中提出的攻击公式的查询复杂度。为完整起见，我们还在附录 A.1 节中比较了这种方法。此外，（Chen et al., 2019）使用单点梯度估计，这是无偏的，但可能遇到比我们论文中梯度估计更大的方差。因此，我们可以在附录 A.1 节中观察到，尽管它们在初始阶段稍快，但 Sign-OPT 会赶上并最终得到一个稍好的解决方案。

提出的方法
我们遵循（Cheng et al., 2019）中的相同公式，并将硬标签攻击视为
寻找到决策边界最短距离的方向的问题。具体来说，对于
给定的样本 $x_0$ ，真实标签 $y_0$ 和硬标签黑盒函数 $R^d \rightarrow \{1, \ldots, K\}$ ，
目标函数 $R^d \rightarrow R$ （对于非目标攻击）可以写为：
$min⁡θg(θ)其中g(θ)=arg⁡min⁡λ>0{f(x0+λθ∥θ∥)≠y0}.\min_{\theta} g(\theta) \quad \text{其中} \quad g(\theta) = \arg\min_{\lambda>0} \left\{ f\left(x_0 + \lambda \frac{\theta}{\|\theta\|}\right) \neq y_0 \right\}.$
(1)
已经表明，这个目标函数通常是平滑的，并且目标函数 $g$ 可以
通过局部的二分搜索过程来评估。在每个二分搜索步骤中，我们查询函数
$f(x0+λθ∥θ∥)f(x_0 + \lambda \frac{\theta}{\|\theta\|})$ ，并根据硬标签预测¹确定在方向 $θ\theta$ 上到决策边界的距离是大于
还是小于 $λ\lambda$ 。

由于目标函数是可计算的， $g$ 的方向导数可以通过有限
差分来估计：
$∇^g(θ;u):=g(θ+ϵu)−g(θ)ϵu\hat{\nabla}g(\theta; u) := \frac{g(\theta + \epsilon u) - g(\theta)}{\epsilon} u$
(2)
其中 $u$ 是一个随机高斯向量， $ϵ>0\epsilon > 0$ 是一个非常小的平滑参数。这是一种用于估计方向导数的标准零阶预言机，基于此，我们可以应用许多不同的零阶优化算法来最小化 $g$ 。例如，Cheng et al. (2019) 使用了随机无导数算法 Nesterov & Spokoiny (2017) 来求解问题 (1)。然而，每次计算 (2) 需要由于二分搜索而需要许多硬标签查询，因此 Chenget al. (2019) 尽管收敛速度快，仍然需要大量查询。在这项工作中，我们介绍了一种算法，极大地改进了相对于 Cheng et al. (2019) 的查询复杂度。我们的算法基于以下关键思想：(i) 为了使算法收敛，并不需要非常精确的方向导数值，以及 (ii) 存在一种不完美但信息丰富的 $g$ 的方向导数估计，可以通过单次查询计算。¹注意二分搜索只在一个小的局部区域有效；在更一般的情况下， $g(θ)g(\theta)$ 必须通过细粒度搜索加二分搜索来计算，如 Cheng et al. (2019) 所述。
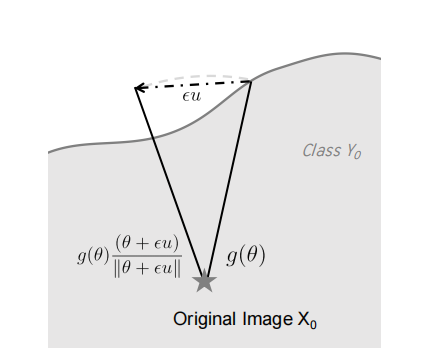
在这里插入图片描述
图 1：示意图

单次查询预言机

如前所述，先前的方法需要计算 $g(θ+ϵu)−g(θ)g(\bm{\theta}+\epsilon\bm{u})-g(\bm{\theta})$ ，这消耗大量查询。然而，基于 $g(⋅)g(\cdot)$ 的定义，我们可以使用单次查询计算该值的符号 $sign(g(θ+ϵu)−g(θ))\text{sign}(g(\bm{\theta}+\epsilon\bm{u})-g(\bm{\theta}))$ 。考虑非目标攻击情况，该符号可以通过下式计算

$f(x0+g(θ)(θ+ϵu)∥θ+ϵu∥)=y0,−1,否则.\text{sign}(g(\bm{\theta}+\epsilon\bm{u})-g(\bm{\theta}))=\begin{cases}+1,&\text{如果 } f(x_{ 0}+g(\bm{\theta})\frac{(\bm{\theta}+\epsilon\bm{u})}{\|\bm{\theta}+\epsilon \bm{u}\|})=y_{0},\\ -1,&\text{否则}.\end{cases}$ (3)

图 1 说明了这一点。本质上，对于一个新方向 $θ+ϵu\bm{\theta}+\epsilon\bm{u}$ ，我们测试在该方向上距离 $x_{0}$ 原始距离 $g(θ)g(\bm{\theta})$ 处的点是否位于决策边界内部或外部，即产生的扰动是否会导致分类器的错误预测。如果产生的扰动在边界外部，即 $f(x0+g(θ)(θ+ϵu)∥θ+ϵu∥)≠y0f(x_{0}+g(\bm{\theta})\frac{(\bm{\theta}+\epsilon\bm{u})}{\|\bm{\theta}+\epsilon \bm{u}\|})\neq y_{0}$ ，则新方向到决策边界的距离更小，因此给出更小的 $g$ 值。这表明 $u\mathbf{u}$ 是减小 $g$ 的下降方向。

Sign-OPT 攻击

通过采样 $Q$ 次随机高斯向量，我们可以通过下式估计不完美的梯度

$∇^g(θ)≈g^:=∑q=1Qsign (g(θ+ϵuq)−g(θ))uq,\hat{\nabla}g(\bm{\theta})\approx\hat{\bm{g}}:=\sum_{q=1}^{Q}\text{sign }(g(\bm{\theta}+\epsilon\mathbf{u}_{q})-g(\bm{\theta}))\mathbf{u}_{q},$ (4)

这只需要 $Q$ 次查询。然后，我们使用这个不完美的梯度估计来更新我们的搜索方向 $θ\bm{\theta}$ ，即 $θ←θ−ηg^\bm{\theta}\leftarrow\bm{\theta}-\eta\hat{\mathbf{g}}$ ，其中步长为 $η\eta$ ，并使用相同的搜索过程以一定的精度计算 $g(θ)g(\bm{\theta})$ 。详细过程如算法 1 所示。

在这里插入图片描述

我们注意到 Liu et al. (2019) 为软标签黑盒攻击（非硬标签设置）设计了一种 Zeroth Order SignSGD 算法。他们使用 $∇^g(θ)≈g^:=∑q=1Qsign(g(θ+ϵuq)−g(θ))uq\hat{\nabla}g(\bm{\theta})\approx\hat{\bm{g}}:=\sum_{q=1}^{Q}\text{ sign}(g(\bm{\theta}+\epsilon\mathbf{u}_{q})-g(\bm{\theta}))\mathbf{u}_{q}$ 并表明，仅使用梯度估计的符号信息，它可以实现与零阶随机梯度下降相当甚至更好的收敛速率。虽然可以将 ZO-SignSGD 与我们提出的单次查询预言机结合来解决硬标签攻击，但他们的估计器将对整个向量取符号，从而忽略了 $uq\mathbf{u}_{q}$ 的方向，这导致在实践中收敛速度较慢（更多细节请参见第 4.4 节和图 5(b)）。

据我们所知，没有先前的分析可以用于证明算法 1 的收敛性。在下文中，我们证明算法 1 实际上可以收敛，并且尽管使用了不同的梯度估计器，但与（Liu et al., 2019）相比具有相似的收敛速率。

假设 1。函数 $g(θ)g(\theta)$ 是 L-平滑的，且 L 值有限。

假设 2。在任何迭代步骤 t，函数 g 的梯度上界为 $∥∇g(θt)∥2≤σ\|\nabla g(\bm{\theta}_{t})\|_{2}\leq\sigma$ 。

定理 3.1。假设假设中的条件成立，并且梯度噪声的分布是单峰且对称的。那么，使用学习率 $ηt=O(1QdT)\eta_{t}=O(\frac{1}{Q\sqrt{dT}})$ 和 $ϵ=O(1dT)\epsilon=O(\frac{1}{dT})$ 的 Sign-OPT 攻击将对 $E[∥∇g(θ)∥2]\mathbb{E}[\|\nabla g(\bm{\theta})\|_{2}]$ 给出以下界限：

$E[∥∇g(θ)∥2]=O(dT+dQ).\mathbb{E}[\|\nabla g(\bm{\theta})\|_{2}]=O\left(\frac{\sqrt{d}}{\sqrt{T}}+\frac{d} {\sqrt{Q}}\right).$

证明可以在附录 A.2 小节中找到。与 Liu et al. (2019) 提供的原始分析的主要区别在于，他们只处理每个元素的符号，而我们的分析还考虑了 $uq\boldsymbol{u}_{q}$ 每个元素的幅度。

其他梯度估计

请注意，通过我们的单次查询预言机计算的值 $sign⁡(g(θ+ϵu)−g(θ))\operatorname{sign}(g(\boldsymbol{\theta}+\epsilon\boldsymbol{u})-g( \boldsymbol{\theta}))$ 实际上是方向导数的符号：

$ϵ.\operatorname{sign}(\langle\nabla g(\boldsymbol{\theta}),\boldsymbol{u}\rangle )=\operatorname{sign}\left(\lim_{\epsilon\rightarrow 0}\frac{g(\boldsymbol{\theta}+\epsilon\boldsymbol{u})-g(\boldsymbol{\theta})}{\epsilon}\right)\approx\operatorname{sign}(g(\boldsymbol{\theta}+\epsilon\boldsymbol{u})-g(\boldsymbol{\theta})) \text{ 对于小的 }\epsilon.$

因此，我们可以使用此信息来估计原始梯度。上一节中的 Sign-OPT 方法使用 $∑qsign⁡(⟨∇g(θ),uq⟩)uq\sum_{q}\operatorname{sign}(\langle\nabla g(\boldsymbol{\theta}),\boldsymbol{u }_{q}\rangle)\boldsymbol{u}_{q}$ 作为梯度的估计。令 $yq:=sign⁡(⟨∇g(θ),uq⟩)y_{q}:=\operatorname{sign}(\langle\nabla g(\boldsymbol{\theta}),\boldsymbol{u }_{q}\rangle)$ ，一个更准确的梯度估计可以转化为以下约束优化问题：

找到一个向量 $z\boldsymbol{z}$ ，使得 $sign⁡(⟨z,uq⟩)=yq∀q=1,…,Q\operatorname{sign}(\langle\boldsymbol{z},\boldsymbol{u}_{q}\rangle)=y_{q} ~~ \forall q=1,\ldots,Q$ 。

因此，这等价于一个硬约束 SVM 问题，其中每个 $uq\boldsymbol{u}_{q}$ 是一个训练样本， $y_{q}$ 是对应的标签。然后可以通过解决以下二次规划问题来恢复梯度：

$min⁡zzTzs.t.zTuq≥yq,∀q=1,…,Q.\min_{\boldsymbol{z}}~ \boldsymbol{z}^{T}\boldsymbol{z} \quad \text{s.t.} \quad \boldsymbol{z}^{T}\boldsymbol{u}_{q} \geq y_{q}, ~~ \forall q=1,\ldots ,Q.$ (5)

通过解决这个问题，我们可以得到梯度的良好估计。如前所述，每个 $y_{q}$ 可以通过单次查询确定。因此，我们提出了 Sign-OPT 的一个变体，称为 SVM-OPT 攻击。详细过程如算法 2 所示。我们将在第 4.1 小节中对我们两种算法进行经验比较。

在这里插入图片描述

4 实验结果

我们在三个不同的标准数据集——MNIST (LeCun et al., 1998)、CIFAR-10 (Krizhevsky et al.) 和 ImageNet-1000 (Deng et al., 2009)——上评估了在硬标签设置下攻击黑盒模型的 SIGN-OPT 算法，并将其与现有方法进行比较。为公平和易于比较，我们使用 (Carlini & Wagner, 2017) 提供的 CNN 网络，该网络也被其他先前的硬标签攻击使用。具体来说，对于 MNIST 和 CIFAR-10，该模型总共由九层组成——四个卷积层、两个最大池化层和两个全连接层。关于实现、训练和参数的更多细节可在 (Carlini & Wagner, 2017) 中找到。如 (Carlini & Wagner, 2017) 和 (Cheng et al., 2019) 所报告，我们能够在 MNIST 上达到 99.5% 的准确率，在 CIFAR-10 上达到 82.5% 的准确率。我们使用 torchvision (Marcel & Rodriguez, 2010) 提供的预训练 Resnet-50 (He et al., 2016) 网络用于 ImageNet-1000，其 Top-1 准确率为 76.15%。

在我们的实验中，我们发现 Sign-OPT 和 SVM-OPT 在查询效率方面表现非常相似。因此，我们仅将 Sign-OPT 攻击与以前的方法进行比较，并在第 4.1 小节中提供 Sign-OPT 和 SVM-OPT 之间的比较。我们比较以下攻击：

*Sign-OPT 攻击 (黑盒): 本文提出的方法。
*基于优化的攻击 (Opt-based attack) (黑盒): Cheng et al. (2019) 中提出的方法，他们使用随机无梯度方法来优化相同的目标函数。我们使用 https://github.com/LeMinhThong/blackbox-attack 提供的实现。
*边界攻击 (Boundary attack) (黑盒): Brendel et al. (2017) 中提出的方法。这仅在 $L_{2}$ 设置中进行比较，因为它是为此设计的。我们使用 Foolbox (https://github.com/bethgelab/foolbox) 中的实现。
*智能猜测攻击 (Guessing Smart Attack) (黑盒): (Brunner et al., 2018) 中提出的方法。该攻击通过将采样偏向三个先验来增强边界攻击。请注意，其中一个先验假设可以访问与目标模型相似的模型，为公平比较，我们在实验中未纳入此偏差。我们使用 https://github.com/ttbrunner/biased_boundary_attack 提供的实现。
*C&W 攻击 (白盒): Carlini & Wagner (2017) 提出的白盒设置中最流行的方法之一。我们使用 C&W $L_{2}$ 范数攻击作为白盒攻击性能的基线。

对于每次攻击，我们从验证集中随机抽取 100 个样本并为它们生成对抗扰动。对于非目标攻击，我们只考虑被模型正确预测的样本；对于目标攻击，我们考虑尚未被预测为目标标签的样本。为了比较不同的方法，我们主要使用_中值失真_作为度量标准。 $x$ 次查询的中值失真是一种方法使用少于 $x$ 次查询实现的所有样本的对抗扰动的中值。由于所有硬标签攻击算法都将从一个对抗样本开始并不断减小失真，如果我们在任何时候停止，它们总是会给出一个对抗样本，因此中值失真是比较它们性能的最合适指标。此外，我们还显示了给定阈值 ( $ϵ\epsilon$ ) 下 $x$ 次查询的_成功率 (SR)_，即在少于 $x$ 次查询的情况下实现低于 $ϵ\epsilon$ 的对抗扰动的样本百分比。我们在不同的阈值上评估成功率，这些阈值取决于所使用的数据集。对于每种设置中不同算法的比较，我们在所有攻击中选择相同的样本集。

实现细节：为了优化算法 1，我们使用 Cheng et al. (2019) 中实现的相同线搜索程序来估计步长 $η\eta$ 。以相对较少的查询次数为代价，这显著加快了优化速度。与 Cheng et al. (2019) 类似，算法 1 最后一步中的 $g(θ)g(\theta)$ 通过二分搜索近似。算法 1 中的初始 $θ0\theta_{0}$ 是通过
在这里插入图片描述

图 2：Sign-OPT 目标攻击示例。 $L_{2}$ 失真和使用的查询次数显示在图像上方和下方。前两行：Sign-OPT 攻击和 OPT 攻击的示例比较。第三和第四行：在 CIFAR-10 和 ImageNet 上的 Sign-OPT 攻击示例。

评估 100 个随机方向上的 $g(θ)g(\theta)$ 并取最佳方向来计算的。我们公开提供了我们的实现²。

脚注 2：https://github.com/cmhcbb/attackbox

Sign-OPT 与 SVM-OPT 的比较

在我们的实验中，我们发现这两种攻击在查询性能方面在所有设置（ $L_2$ /L_{\infty}$ 和目标/非目标）和数据集上都非常相似。我们在图 3 中展示了 MNIST 和 CIFAR-10（基于 $L_2$ 范数）上目标和非目标攻击的比较。我们看到，对于给定的查询次数，Sign-OPT 和 SVM-OPT 实现的中值失真非常接近。

每次梯度估计的查询次数：在图 3 中，我们展示了具有不同 $Q$ 值的 Sign-OPT 攻击的比较。我们的实验表明， $Q$ 对算法达到的收敛点没有影响。然而， $Q$ 值小会提供嘈杂的梯度估计，因此延迟了收敛到对抗扰动。另一方面， $Q$ 值大则需要每次梯度估计花费大量时间。在一小部分样本上进行微调后，我们发现 $Q = 200$ 在两者之间提供了良好的平衡。因此，我们在本节的所有实验中将 $Q$ 的值设置为 200。

非目标攻击

在此攻击中，目标是从原始图像生成一个对抗样本，使得模型对其的预测与原始图像不同。图 4 详细比较了三种数据集上 $L_2$ 情况下不同攻击的效果。Sign-OPT 攻击在查询次数方面 consistently 优于当前的方法。Sign-OPT 不仅在查询方面更高效，在大多数情况下，它收敛到的失真度也低于其他硬标签攻击所能达到的水平。此外，我们观察到 Sign-OPT 收敛到一个与 C&W 白盒攻击相当的解决方案（在 CIFAR-10 上更好，在 MNIST 上稍差，在 ImageNet 上相当）。这对于硬标签攻击算法来说意义重大，因为我们获得的信息非常有限。

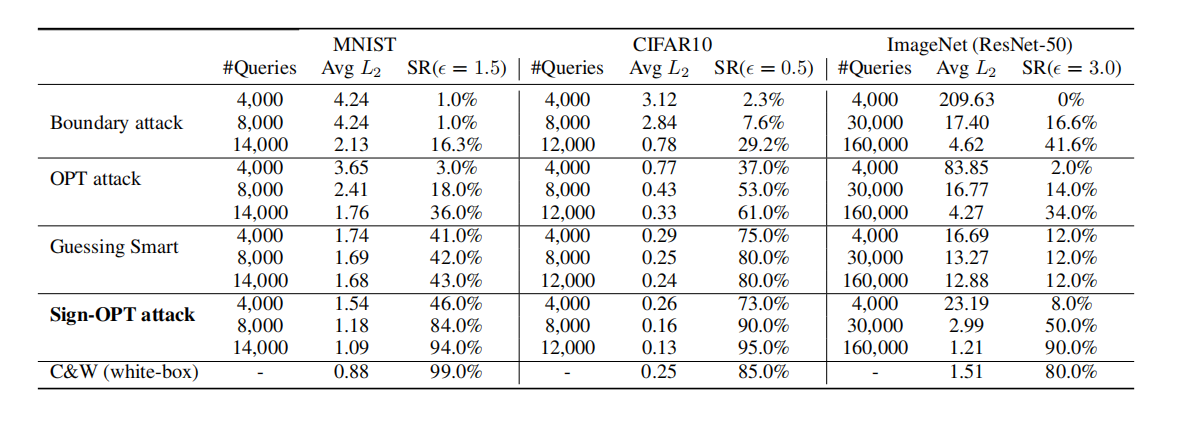
我们在表 1 中重点比较了边界攻击、基于优化的攻击 (OPT-based attack) 和 Sign-OPT 攻击（基于 $L_2$ 范数）的一些结果。特别是在 ImageNet 数据集上的 ResNet-50 模型，Sign-OPT 攻击在少于 $30 k$ 次查询内达到低于 3.0 的中值失真，而其他攻击需要超过 $200 k$ 次查询才能达到相同水平。

目标攻击

在目标攻击中，目标是为图像生成一个对抗扰动，使得结果图像的预测与指定的目标相同。对于每个样本，我们随机指定目标标签，并在不同攻击中保持一致。我们使用训练数据集中目标标签类的 100 个样本来计算算法 1 中的初始 $θ0\theta_0$ ，并且这个 $θ0\theta_0$ 在不同攻击中是相同的。图 2 显示了一些由 Sign-OPT 攻击和基于优化的攻击生成的对抗样本示例。前两行分别显示了在 MNIST 数据集的一个样本上 Sign-OPT 和 Opt 攻击的比较。图表显示了两者在几乎

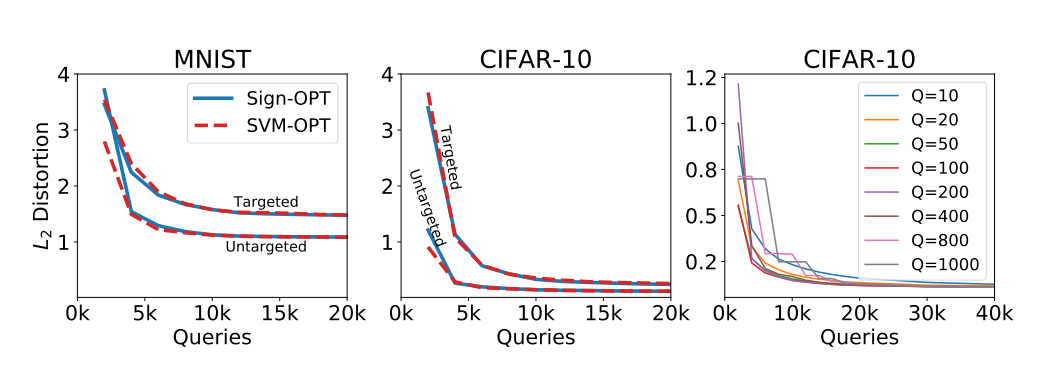
在这里插入图片描述

图 3：中值 $L_2$ 失真 vs 查询次数。前两个：MNIST 和 CIFAR-10 上 Sign-OPT 和 SVM-OPT 攻击的比较。第三个：不同 $Q$ 值下 Sign-OPT 的性能。

相同的查询次数下生成的对抗样本。对于这个特定示例，Sign-OPT 方法在 $∼6k\sim 6k$ 次查询内生成了 $L_2$ 对抗扰动为 0.94 的样本，而基于优化的攻击需要 $∼35k\sim 35k$ 次查询。图 5 显示了目标设置下不同攻击的比较。在我们的实验中，白盒攻击 C&W 在 MNIST 数据集上达到的平均失真为 1.51，Sign-OPT 需要 $∼12k\sim 12k$ 次查询，而其他攻击需要 $> 120 k$ 次查询。我们在图 6 中展示了 CIFAR-10 数据集上不同攻击在目标和非目标情况下的成功率比较。

单次查询预言机的能力

在本小节中，我们进行了几个实验来证明我们提出的单次查询预言机在硬标签对抗攻击设置中的有效性。ZO-SignSGD 算法（Liu et al., 2019）是为软标签黑盒攻击提出的，我们将其扩展到硬标签设置。一种直接的方法是简单地将 ZO-SignSGD 应用于求解 Cheng et al. (2019) 提出的硬标签目标，使用（Cheng et al., 2019）中的二分搜索估计梯度并取其符号。在图 5(b) 中，我们清楚地观察到，简单地将 ZO-SignSGD 和 Cheng et al. (2019) 结合起来效率不高。利用提出的单次查询符号预言机，我们也可以减少这种方法的查询计数，如图 5(b) 所示。这验证了单次查询预言机的有效性，它可以普遍改进硬标签攻击设置中的许多不同优化方法。需要注意的是，Sign-OPT 相对于使用单次查询预言机的 ZO-SignSGD 仍有改进，因为

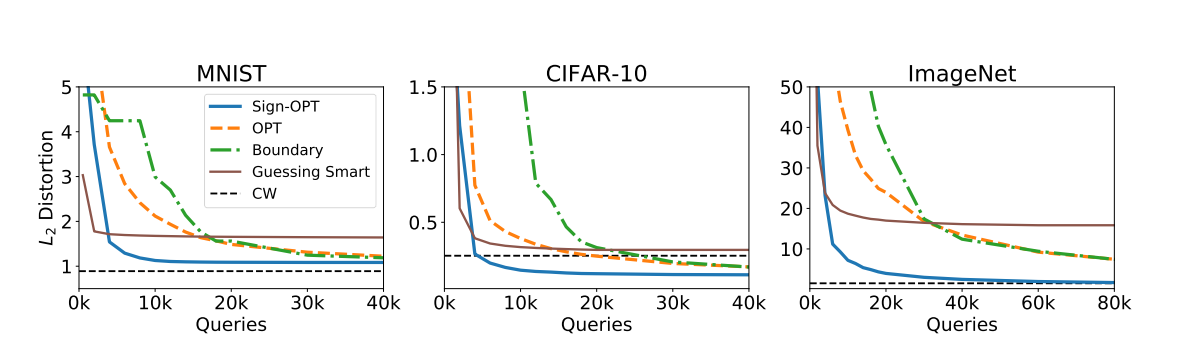
在这里插入图片描述

图 4：非目标攻击：不同数据集的中值失真 vs 查询次数。

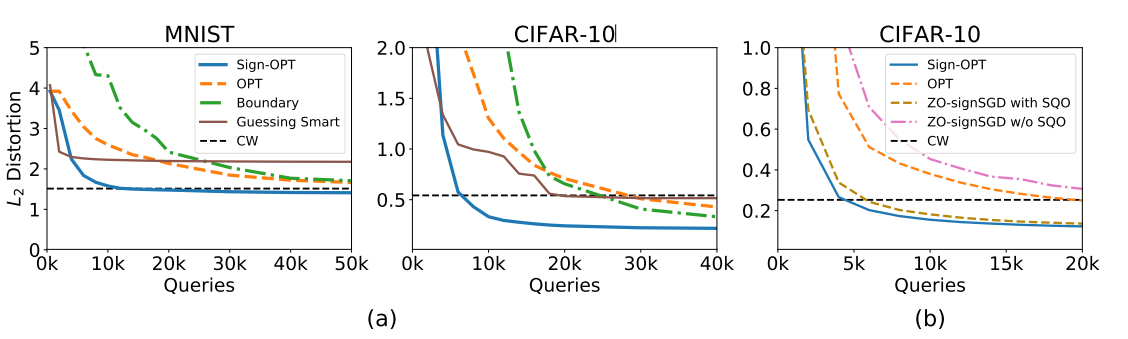
在这里插入图片描述

图 5: (a) 目标攻击：MNIST 和 CIFAR-10 上不同攻击的中值失真 vs 查询次数。(b) 比较使用和不使用单次查询预言机 (SQO) 的 Sign-OPT 和 ZO-SignSGD。
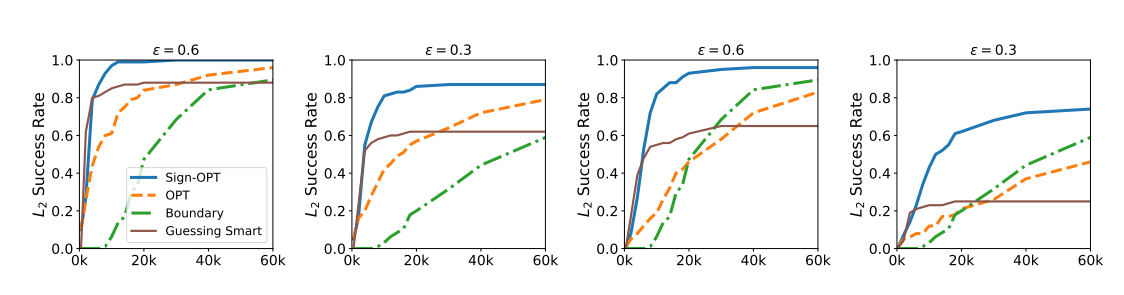
在这里插入图片描述

图 6: CIFAR-10 的成功率 vs 查询次数（基于 $L_2$ 范数攻击）。前两个和后两个分别描述了非目标和目标攻击。成功率阈值在每个图的顶部。

我们的算法不仅直接获取梯度估计的符号，还利用了随机方向 $u$ 的尺度。换句话说，signSGD 的梯度范数始终为 1，而我们的梯度范数考虑了 $u$ 的幅度。因此，我们的 signOPT 优化算法与 (Liu et al., 2019) 或任何其他提出的 signSGD 变体根本不同。我们的方法可以看作是一种新的零阶优化算法，具有 signSGD 快速收敛的特点。

5 结论

我们为硬标签黑盒设置下的对抗攻击开发了一种新的、超查询高效的算法。利用 Cheng et al. (2019) 中相同的平滑重构，我们设计了一种新颖的零阶预言机，可以使用单次查询计算攻击目标的方向导数符号。借助这种单次查询预言机，我们设计了一种新的优化算法，与 Cheng et al. (2019) 相比，可以 dramatically 减少查询次数。我们证明了所提出算法的收敛性，并表明我们的新算法远远优于当前的硬标签黑盒攻击。

致谢

这项工作基于能源部国家能源技术实验室根据奖励号 DE-SC0000911 以及 NSF 根据 IIS1719097 支持的工作。

表 1： $L_{2}$ 非目标攻击 - 比较不同攻击使用给定查询次数达到的平均 $L_{2}$ 失真。SR 代表成功率。

在这里插入图片描述

参考文献

Al-Dujaili and O’Reilly (2019) Abdullah Al-Dujaili and Una-May O’Reilly. There are no bit parts for sign bits in black-box attacks. arXiv preprint arXiv:1902.06894, 2019.
Alzantot et al. (2019) Moustafa Alzantot, Yash Sharma, Supriyo Chakraborty, Huan Zhang, Cho-Jui Hsieh, and Mani B Srivastava. Genattack: Practical black-box attacks with gradient-free optimization. In Proceedings of the Genetic and Evolutionary Computation Conference, pp. 1111–1119, 2019.
Athalye et al. (2018) Anish Athalye, Nicholas Carlini, and David Wagner. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. In ICML, 2018.
Bernstein et al. (2018) Jeremy Bernstein, Yu-Xiang Wang, Kamyar Azizzadenesheli, and Animashree Anandkumar. signSGD: Compressed optimisation for non-convex problems. In Jennifer Dy and Andreas Krause (eds.), Proceedings of the 35th International Conference on Machine Learning, volume 80 of Proceedings of Machine Learning Research, pp. 560–569, Stockholmsmassan, Stockholm Sweden, 10-15 Jul 2018. PMLR. URL http://proceedings.mlr.press/v80/bernstein18a.html.
Brendel et al. (2017) Wieland Brendel, Jonas Rauber, and Matthias Bethge. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. arXiv preprint arXiv:1712.04248, 2017.
Brunner et al. (2018) Thomas Brunner, Frederik Diehl, Michael Truong Le, and Alois Knoll. Guessing smart: Biased sampling for efficient black-box adversarial attacks. arXiv preprint arXiv:1812.09803, 2018.
Carlini & Wagner (2017) Nicholas Carlini and David Wagner. Towards evaluating the robustness of neural networks. In Security and Privacy (SP), 2017 IEEE Symposium on, pp. 39–57. IEEE, 2017.
Chen et al. (2019) Jianbo Chen, Michael I. Jordan, and Martin J. Wainwright. Hopskipjumpattack: A query-efficient decision-based attack. arXiv preprint arXiv:1904.02144, 2019.
Chen et al. (2017) Pin-Yu Chen, Huan Zhang, Yash Sharma, Jinfeng Yi, and Cho-Jui Hsieh. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, pp. 15–26. ACM, 2017.
Chen et al. (2018) Pin-Yu Chen, Yash Sharma, Huan Zhang, Jinfeng Yi, and Cho-Jui Hsieh. Ead: elastic-net attacks to deep neural networks via adversarial examples. In Thirty-second AAAI conference on artificial intelligence, 2018.
Cheng et al. (2019) Minhao Cheng, Thong Le, Pin-Yu Chen, Huan Zhang, Jinfeng Yi, and Cho-Jui Hsieh. Query-efficient hard-label black-box attack: An optimization-based approach. In International Conference on Learning Representations, 2019. URL https://openreview.net/forum?id=rJlk6iRqKX.
Deng et al. (2009) Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on, pp. 248–255. IEEE, 2009.
Duchi et al. (2012) John C Duchi, Peter L Bartlett, and Martin J Wainwright. Randomized smoothing for stochastic optimization. SIAM Journal on Optimization, 22(2):674–701, 2012.
Goodfellow et al. (2015) Ian Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In International Conference on Learning Representations, 2015.
He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778, 2016.
Ilyas et al. (2018a) Andrew Ilyas, Logan Engstrom, Anish Athalye, and Jessy Lin. Black-box adversarial attacks with limited queries and information. In International Conference on Machine Learning, pp. 2142–2151, 2018a.

===== Page 11 =====

Ilyas et al. (2018b) Andrew Ilyas, Logan Engstrom, and Aleksander Madry. Prior convictions: Black-box adversarial attacks with bandits and priors. arXiv preprint arXiv:1807.07978, 2018b.
Jun et al. (2018) Kwang-Sung Jun, Lihong Li, Yuzhe Ma, and Jerry Zhu. Adversarial attacks on stochastic bandits. In Advances in Neural Information Processing Systems, pp. 3640–3649, 2018.
Krizhevsky et al. (2016) Alex Krizhevsky, Vinod Nair, and Geoffrey Hinton. Cifar-10 (canadian institute for advanced research). URL http://www.cs.toronto.edu/~kriz/cifar.html.
Kurakin et al. (2016) Alexey Kurakin, Ian Goodfellow, and Samy Bengio. Adversarial machine learning at scale. arXiv preprint arXiv:1611.01236, 2016.
LeCun et al. (1998) Yann LeCun, Leon Bottou, Yoshua Bengio, Patrick Haffner, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
Liu et al. (2018) Sijia Liu, Bhavya Kailkhura, Pin-Yu Chen, Paishun Ting, Shiyu Chang, and Lisa Amini. Zeroth-order stochastic variance reduction for nonconvex optimization. In S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (eds.), Advances in Neural Information Processing Systems 31, pp. 3727–3737. Curran Associates, Inc., 2018. URL http://papers.nips.cc/paper/7630-zeroth-order-stochastic-variance-reduction-for-nonconvex-optimization.pdf.
Liu et al. (2019) Sijia Liu, Pin-Yu Chen, Xiangyi Chen, and Mingyi Hong. signSGD via zeroth-order oracle. In International Conference on Learning Representations, 2019. URL https://openreview.net/forum?id=BJe-DsC5Fm.
Madry et al. (2017) Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and Adrian Vladu. Towards deep learning models resistant to adversarial attacks. arXiv preprint arXiv:1706.06083, 2017.
Marcel & Rodriguez (2010) Sebastien Marcel and Yann Rodriguez. Torchvision the machine-vision package of torch. In Proceedings of the 18th ACM International Conference on Multimedia, MM '10, pp. 1485–1488, New York, NY, USA, 2010. ACM. ISBN 978-1-60558-933-6. doi: 10.1145/1873951.1874254. URL http://doi.acm.org/10.1145/1873951.1874254.
Nesterov & Spokoiny (2017) Yurii Nesterov and Vladimir Spokoiny. Random gradient-free minimization of convex functions. Foundations of Computational Mathematics, 17(2):527–566, 2017.
Papernot et al. (2017) Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay Celik, and Ananthram Swami. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, pp. 506–519. ACM, 2017.
Szegedy et al. (2016) Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jon Shlens, and Zbigniew Wojna. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2818–2826, 2016.
Tu et al. (2019) Chun-Chen Tu, Paishun Ting, Pin-Yu Chen, Sijia Liu, Huan Zhang, Jinfeng Yi, Cho-Jui Hsieh, and Shin-Ming Cheng. Autozoom: Autoencoder-based zeroth order optimization method for attacking black-box neural networks. AAAI, 2019.
Zhang et al. (2019) Huan Zhang, Hongge Chen, Zhao Song, Duane Boning, Inderjit S Dhillon, and Cho-Jui Hsieh. The limitations of adversarial training and the blind-spot attack. arXiv preprint arXiv:1901.04684, 2019.