图解快速排序C语言实现
1 快速排序
快速排序(Quick Sort)是由英国计算机科学家Tony Hoare于1959年提出的一种高效的排序算法。
1.1 基本概念与理解
快速排序采用分治策略(Divide and Conquer)将问题分解为更小的子问题来解决。快速排序的核心思想是:
1.选取基准值(pivot):从待排序序列中选择一个元素作为基准
2.分区操作(partition):将序列重新排列,所有比基准值小的元素放在基准前面,比基准值大的元素放在基准后面
3.递归排序:对基准值左右两个子序列递归地进行快速排序
快速排序是原地排序算法,不需要额外的存储空间,平均情况下具有极佳的性能表现。
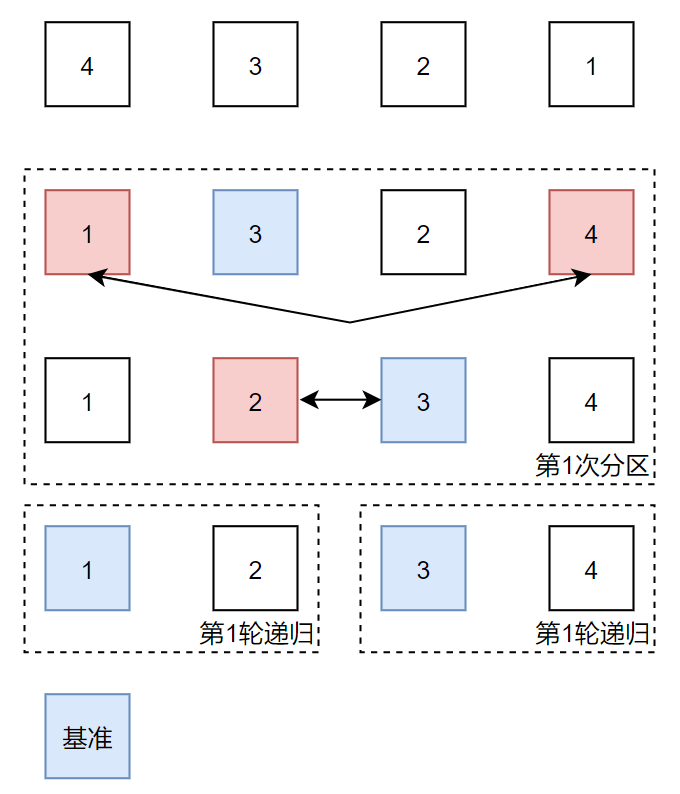
1.2 算法执行过程
初始调用阶段
1.初始参数:首次调用时left=0(数组起始),right=n-1(数组末尾)
2.终止检查:检查left>=right条件,防止空数组或单元素数组
分区过程详解
1.基准选择:计算中间索引(left+right)/2并取该位置元素作为基准值p
2.双指针初始化:
(1)i从最左端(left)开始向右扫描
(2)j从最右端(right)开始向左扫描
3.扫描阶段:
(1)左指针i向右移动,直到找到≥p的元素
(2)右指针j向左移动,直到找到≤p的元素
4.元素交换:
(1)当i和j都停止时,若i <= j则交换arr[i]和arr[j]
(2)交换后同时移动两个指针(i++, j–)
递归调用阶段
1.分区完成:当i越过j时,数组被划分为三部分:
[left…j]:所有元素≤基准值
[i…right]:所有元素≥基准值
中间重叠区已有序
2.递归排序:
先对左子数组[left…j]递归调用quick_sort
再对右子数组[i…right]递归调用quick_sort
执行示例(数组[5,2,9,3,7])
1.第一次调用:
基准p=9(中间元素)
分区后:[5,2,7,3,9]
递归调用左[5,2,7,3]和右[9]
2.左子数组[5,2,7,3]:
基准p=2(中间元素)
分区后:[2,5,7,3]
递归调用左[2]和右[5,7,3]
3.右子数组[5,7,3]:
基准p=7
分区后:[5,3,7]
递归调用左[5,3]和右[7]
4.最终结果:所有递归完成后得到有序数组[2,3,5,7,9]
1.3 算法复杂度分析
1.时间复杂度
最优情况:每次分区都能将数组均分为两部分,递归树高度为log₂n,每层比较次数为n,时间复杂度为O(nlogn)
平均情况:随机化版本的快速排序平均时间复杂度为O(nlogn)
最坏情况:当数组已有序或逆序时,每次分区只能减少一个元素,时间复杂度退化为O(n²)
2.空间复杂度
快速排序是原地排序,不需要额外存储空间
递归调用栈的深度决定了空间复杂度:
最优情况:O(log n)
最坏情况:O(n)
3. 稳定性分析
快速排序是不稳定的排序算法,因为在分区过程中,相等元素的相对位置可能会改变。
1.4 C语言实现快速排序
#include <stdio.h>#define SORT_DATA_TYPE int/*** @brief 打印数据** @param arr 数组* @param n 数组元素个数*/
void print_array(int arr[], int n)
{int i;for (i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}/*** @brief 快速排序** @param arr 待排序的数组* @param left 数组的左边界索引* @param right 数组的右边界索引*/
void quick_sort(SORT_DATA_TYPE arr[], int left, int right)
{int i = left;int j = right;SORT_DATA_TYPE p = arr[(left + right) / 2];SORT_DATA_TYPE temp;if (left >= right){/* 排序完成 */return;}while (i <= j){/*把小于中间基准值的数放到数组左边把大于中间基准值的数放到数组右边*/while (arr[i] < p){i++;}while (arr[j] > p){j--;}if (i <= j){/*交换数据,即小的放左边,大的放右边*/temp = arr[i];arr[i] = arr[j];arr[j] = temp;i++;j--;}}print_array(&arr[left], right - left + 1); /* 打印数组,调试使用 */quick_sort(arr, left, j);quick_sort(arr, i, right);
}int main()
{SORT_DATA_TYPE arr[] = {4, 3, 2, 1};int n = sizeof(arr) / sizeof(arr[0]);printf("old arr : ");print_array(arr, n);quick_sort(arr, 0, n - 1);printf("new arr : ");print_array(arr, n);return 0;
}
注:
不同类型的数组直接将SORT_DATA_TYPE全部替换为需要的类型,然后删除多余的宏定义即可支持任意类型数组的快速排序。
1.5 简单测试
通过使用数组[4,3,2,1]演示快速排序的执行过程:
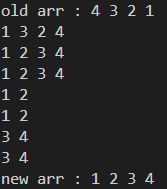
可以使用如下图片演示这一过程: