数据结构----八大排序算法
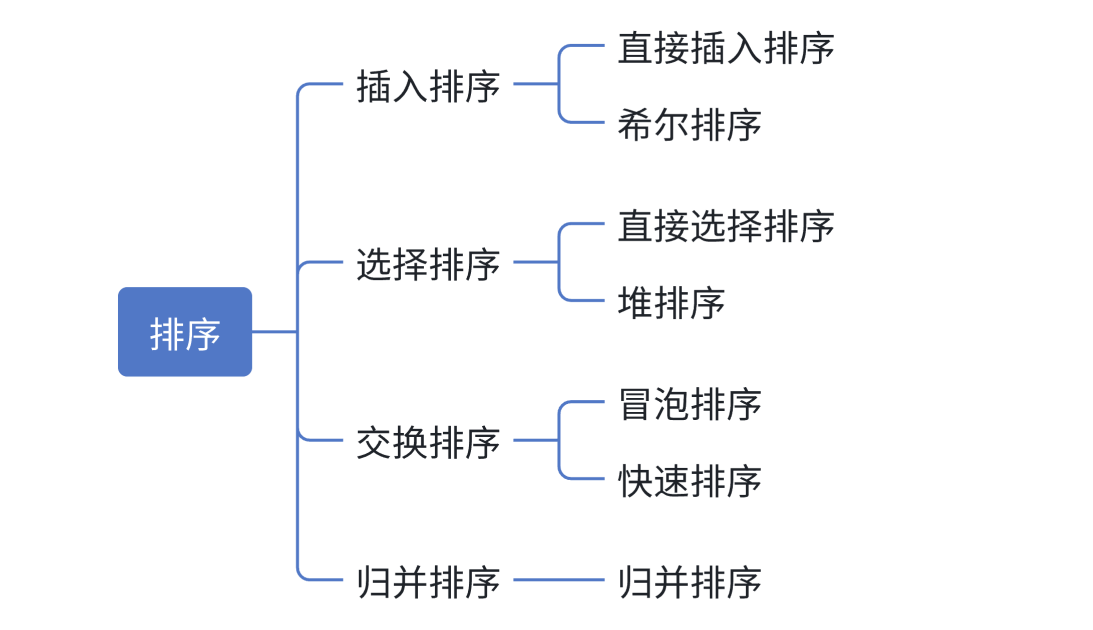
目录
插入排序
直接插入排序
代码实现:
核心思想:
时间(空间)复杂度
时间复杂度
空间复杂度
希尔排序(又称缩小增量法)
核心思想:
代码实现:
时间(空间)复杂度
选择排序
直接选择排序
核心思想:
实现代码:
时间复杂度与空间复杂度
特点:
堆排序
代码实现:
排序原理:
特点:
交换排序
冒泡排序
代码实现:
特点(复杂度):
快速排序
代码实现1(hoare版本):
思路:
注意:
代码实现2(挖坑法):
思路:
代码实现3(lomuto前后指针):
思路:
非递归版本的快速排序(借助数据结构---栈)
代码实现:
优点:
复杂度:
时间复杂度
空间复杂度
归并排序
算法思想:
代码实现:
复杂度:
时间复杂度
空间复杂度
稳定性
计数排序
代码实现:
时间复杂度
空间复杂度
特点:
排序比较:
测试代码(不运行):
插入排序
直接插入排序
代码实现:
#include<stdio.h>
//直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n-1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (tmp <arr[end]){arr[end+1] = arr[end];arr[end] = tmp;end--;}else {break;}}arr[end + 1] = tmp;}
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);InsertSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test();return 0;
}可简化:
// 修正后的直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1]; // 暂存待插入元素// 从后往前找插入位置,大于tmp的元素后移while (end >= 0 && tmp < arr[end]){arr[end + 1] = arr[end]; // 元素后移,给tmp腾位置end--;}arr[end + 1] = tmp; // 将tmp插入到正确位置}
}- 移除了
while循环中的arr[end] = tmp;交换操作,仅保留arr[end + 1] = arr[end];实现元素后移。 - 循环结束后,通过
arr[end + 1] = tmp;一次性将暂存的tmp插入到正确位置,符合直接插入排序的逻辑。
核心思想:
将待插入元素 tmp 暂存,然后将大于 tmp 的元素依次后移,最后将 tmp 插入到正确位置。
时间(空间)复杂度
时间复杂度
-
最佳情况:
O(n)
当数组已经完全有序时,每次插入元素只需与已排序序列的最后一个元素比较一次(无需移动元素),总比较次数为n-1,时间复杂度为线性级。 -
最坏情况:
O(n²)
当数组完全逆序时,每次插入第i个元素(从第 2 个元素开始),需要与已排序序列的i-1个元素全部比较,并将它们依次后移。总操作次数为1+2+3+...+(n-1) = n(n-1)/2,时间复杂度为平方级。 -
平均情况:
O(n²)
对于随机无序的数组,每次插入元素的平均比较和移动次数约为n/2,总操作次数约为n²/4,时间复杂度仍为平方级。
空间复杂度
O(1)(原地排序),且排序稳定
希尔排序(又称缩小增量法)
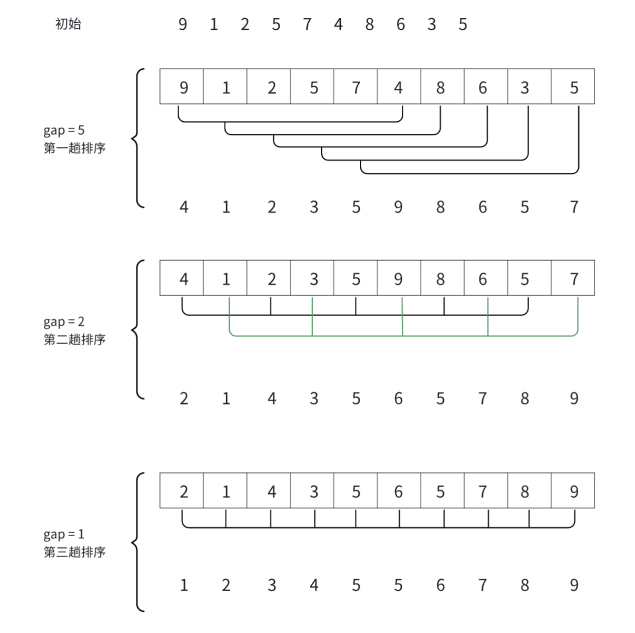
核心思想:
先将整个数组分割成若干个子序列,对每个子序列进行插入排序;逐渐缩小分组间隔,重复排序过程;最后当间隔为 1 时,进行一次完整的插入排序,此时数组已基本有序,效率极高。
代码实现:
#include<stdio.h>
//希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//对每组数据插入排序for (int i = 0; i < n-gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0 && tmp < arr[end]){arr[end + gap] = arr[end];end-=gap;}arr[end + gap] = tmp;}}
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);ShellSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}时间(空间)复杂度
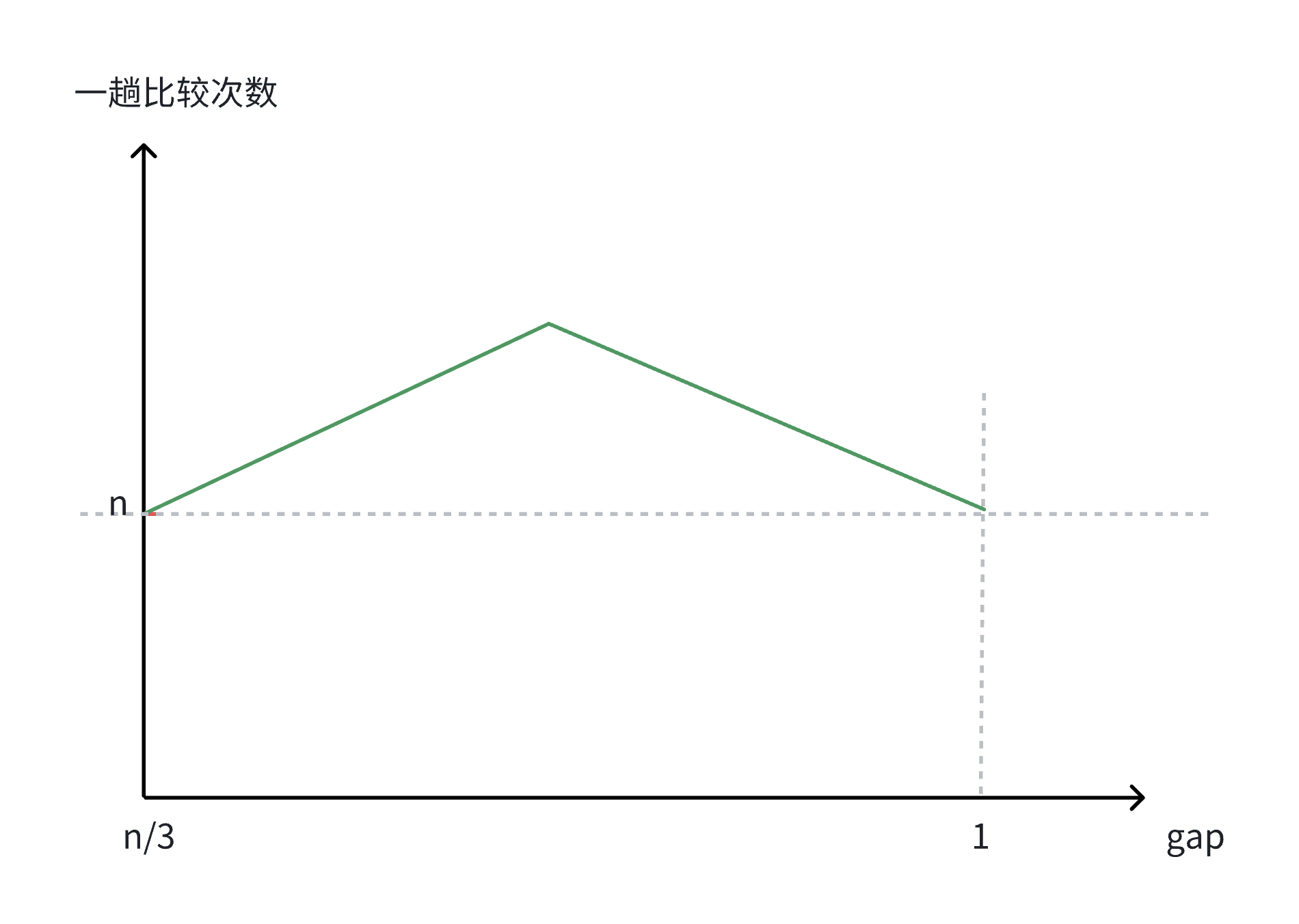
希尔排序的时间复杂度取决于增量序列的选择,目前尚未有严格的数学证明,常见分析如下:
- 若使用增量序列
n/2, n/4, ..., 1,时间复杂度约为 O(n²)(最坏情况); - 若使用更优的增量序列(如 Hibbard 序列
2^k - 1),时间复杂度可降至 O(n^(3/2)) 或更低。
总体而言,希排序的效率远高于直接插入排序,尤其适合中大型数组。


空间复杂度:o(1)
选择排序
直接选择排序
核心思想:
每次从待排序的元素中找到最小(或最大)的元素,将其与待排序部分的第一个元素(最后一个)交换位置,逐渐缩小待排序范围,直到整个数组有序。
实现代码:
#include<stdio.h>
//直接选择排序
void SelectSort(int* arr, int n)
{int begin = 0;int end = n - 1;while (begin < end){int maxi = begin;int mini = begin;for (int i = begin + 1; i <= end; i++){if (arr[i] < arr[mini]){mini = i;}if (arr[i] > arr[maxi]){maxi = i;}}if (maxi == begin){maxi = mini;}Swap(&arr[mini], &arr[begin]);Swap(&arr[maxi], &arr[end]);begin++;end--;}
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);SelectSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}时间复杂度与空间复杂度
-
时间复杂度:
无论数组是否有序,都需要遍历待排序部分寻找最小元素,因此最佳、最坏、平均情况均为 O (n²)。 -
空间复杂度:
仅需常数级额外空间(用于交换元素),因此为 O(1)(原地排序)。
特点:
-
不稳定性:
当待排序部分存在多个相同元素时,交换可能改变它们的相对位置。例如[3, 2, 3, 1]中,第一个3会与1交换,导致两个3的相对位置反转。 -
交换次数少:
每轮排序只需要一次交换(找到最小元素后),总交换次数为n-1次,远少于冒泡排序。 -
适用场景:
适合小规模数据排序,或对交换操作成本较高的场景(因交换次数少)。
堆排序
代码实现:
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//二叉树结构
typedef int HPDataType;
typedef struct heap
{HPDataType* arr;int size; //有效数据个数int capacity; //空间大小
}HP;//交换
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}//向下调整算法
void AdjustDown(HPDataType* arr, int parent, int n)
{int child = parent * 2 + 1;//左孩子while (child < n){//大堆:<//小堆:>if (child + 1 < n && arr[child] < arr[child + 1]){child++;}//大堆: >//小堆:<if (arr[child] > arr[parent]){//调整Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapSort(int* arr, int n)
{//建堆---向下调整法----这里是建大堆for (int i = (n - 2) / 2; i >= 0; i--){AdjustDown(arr, i, n);}//堆排序---如果上面是建小堆,后面这一段不用写都行int end =n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}-
排序原理:
- 先将无序数组构建成大堆(堆顶为最大值)
- 反复将堆顶最大值与未排序部分的末尾元素交换
- 调整剩余元素保持堆结构,直到所有元素排序完成
特点:
- 时间复杂度:O (n log n)(建堆 O (n) + 排序过程 O (n log n))
- 空间复杂度:O (1)(原地排序)
- 稳定性:不稳定排序(交换过程可能改变相等元素的相对位置)
交换排序
冒泡排序
代码实现:
#include<stdio.h>//冒泡排序
void BubbleSort(int* arr, int n)
{for (int i = 0; i < n; i++){for (int j = 0; j < n - i - 1; j++){if (arr[j] > arr[j + 1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;}}}
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);BubbleSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}可升级
// 冒泡排序(升序)
void BubbleSort(int* arr, int n) {// 控制排序的轮数for (int i = 0; i < n - 1; i++) {int flag = 0; // 标记本轮是否发生交换// 每轮比较相邻元素,将较大的元素"冒"到后面for (int j = 0; j < n - 1 - i; j++) {if (arr[j] > arr[j + 1]) {Swap(&arr[j], &arr[j + 1]);flag = 1; // 发生了交换}}// 如果本轮没有交换,说明数组已经有序,提前退出if (flag == 0) {break;}}
}用flag标记,避免过度浪费时间
特点(复杂度):
- 时间复杂度:
- 最坏情况(完全逆序):O (n²)
- 最好情况(已经有序):O (n)(因为有 flag 优化)
- 平均情况:O (n²)
- 空间复杂度:O (1),只需要常数级的额外空间
- 稳定性:稳定排序,相等元素的相对位置不会改变
- 效率较低,适合小规模数据的排序场景
快速排序
代码实现1(hoare版本):
#include<stdio.h>
//hoare版本--找基准值
int _QuickSort(int* arr, int left, int right)
{int keyi = left;++left;while (left <= right){//right:从右往左走,找比基准值小的while (left <= right && arr[right] > arr[keyi]){right--;}while (left <= right && arr[left] < arr[keyi]){left++;}if (left <= right){Swap(&arr[right--], &arr[left++]);}}Swap(&arr[keyi], &arr[right]);return right;
}//快速排序
void QuickSort(int* arr, int left,int right)
{if (left >= right){return;}//找基准值int keyi = _QuickSort(arr, left, right);QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);QuickSort(a,0,n-1);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}思路:

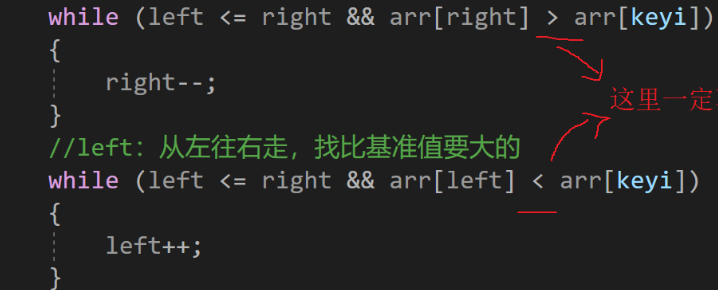
- 右指针逻辑:从右侧开始,跳过所有大于基准值的元素,直到找到第一个小于基准值的元素(或指针交叉)。
- 左指针逻辑:从左侧开始,跳过所有小于基准值的元素,直到找到第一个大于基准值的元素(或指针交叉)。
- 交换操作:当左右指针都找到目标元素且未交叉时,交换这两个元素,确保小元素在左、大元素在右,然后指针继续移动。
- 当
left > right时,循环结束,right的位置就是基准值的正确位置(此时right左侧全是小于基准值的元素,右侧全是大于基准值的元素)。 - 交换基准值(初始在
keyi)和right位置的元素,完成基准值归位。 - 返回
right(基准值最终索引),用于后续递归排序基准值左侧和右侧的子数组。
注意:
找基准值处,判断条件中,不能取等号

代码实现2(挖坑法):
#include<stdio.h>// 交换函数
// void Swap(int* a, int* b) {
// int tmp = *a;
// *a = *b;
// *b = tmp;
// }// 挖坑法求基准值位置
int _QuickSort(int* arr, int left, int right)
{int hole = left; // 初始坑位置(基准值位置)int keyi = arr[hole]; // 缓存基准值while (left < right){// 右指针找小于基准值的元素,填左坑while (left < right && arr[right] >= keyi){--right;}arr[hole] = arr[right];hole = right; // 更新坑位置// 左指针找大于基准值的元素,填右坑while (left < right && arr[left] <= keyi){++left;}arr[hole] = arr[left];hole = left; // 更新坑位置}arr[hole] = keyi; // 最后一个坑填入基准值return hole; // 返回基准值位置
}// 快速排序递归入口
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}int keyi = _QuickSort(arr, left, right);QuickSort(arr, left, keyi - 1); // 排序左半部分QuickSort(arr, keyi + 1, right); // 排序右半部分
}// 打印数组
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}// 测试函数
void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n); // 输出:5 3 9 6 2 4 7 1 8 QuickSort(a, 0, n - 1);printf("排序之后:");arrprint(a, n); // 输出:1 2 3 4 5 6 7 8 9
}int main()
{test01();return 0;
}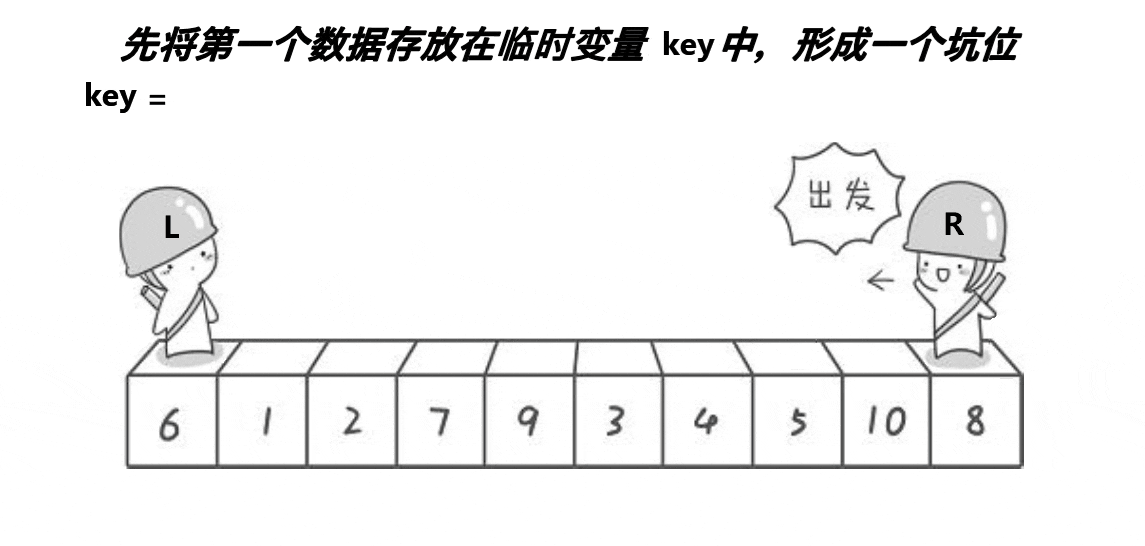
思路:
- 核心思想:通过 "挖坑 - 填坑" 的方式实现分区。初始将基准值位置视为 "坑",然后从右向左找小于基准值的元素填左坑,再从左向右找大于基准值的元素填右坑,最终将基准值填入最后一个坑中。
代码实现3(lomuto前后指针):
思路:


#include <stdio.h>// 交换函数
void Swap(int* a, int* b) {int tmp = *a;*a = *b;*b = tmp;
}// Lomuto前后指针法分区(返回基准值位置)
int _QuickSort(int* arr, int left, int right) {int keyi = left; // 基准值位置(最左元素)int prev = left; // 前指针int cur = prev + 1; // 后指针while (cur <= right) {// 找到小于基准值的元素,移动到左侧区域if (arr[cur] < arr[keyi] && ++prev != cur) {Swap(&arr[prev], &arr[cur]);}cur++;}// 基准值归位Swap(&arr[keyi], &arr[prev]);return prev; // 返回基准值最终位置
}// 快速排序入口(递归)
void QuickSort(int* arr, int left, int right) {if (left >= right) {return; // 区间为空或单个元素,无需排序}// 分区并获取基准值位置int keyi = _QuickSort(arr, left, right);// 递归排序左右子区间QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}// 打印数组
void arrprint(int* arr, int n) {for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");
}// 测试
int main() {int a[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};int n = sizeof(a) / sizeof(a[0]);printf("排序前:");arrprint(a, n);QuickSort(a, 0, n - 1);printf("排序后:");arrprint(a, n); // 输出:1 2 3 4 5 6 7 8 9return 0;
}
核心逻辑:
- 核心逻辑:
cur逐个扫描元素,当遇到小于基准值的元素时,先将prev右移(扩大 “小于区域”),如果此时prev和cur不在同一位置(说明中间有大于基准值的元素),则交换两者的元素,确保小元素被纳入左侧区域。 - 例如:若数组为
[5,3,9,6,2](基准值 5),当cur指向 3(小于 5)时,prev右移到索引 1,与cur重合,不交换;当cur指向 2(小于 5)时,prev右移到索引 2,与cur(索引 4)不重合,交换后数组变为[5,3,2,6,9],左侧区域正确包含小于 5 的元素。 - 遍历结束后,
prev指向 “小于基准值区域” 的最后一个元素,将基准值(初始在keyi)与prev位置的元素交换,此时基准值左侧全是小于它的元素,右侧全是大于等于它的元素。 - 返回
prev(基准值的最终索引),用于外层递归排序左侧[left, prev-1]和右侧[prev+1, right]区间。
非递归版本的快速排序(借助数据结构---栈)
代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
//定义栈的结构
typedef int STDataType;
typedef struct Stack
{STDataType* arr;int top;//有效数据个数int capacity;//容量
}ST;
// 交换函数
void Swap(int* a, int* b)
{int temp = *a;*a = *b;*b = temp;
}
//初始化
void StackInit(ST* ps)
{assert(ps);ps->arr = NULL;ps->top = ps->capacity = 0;
}
// 销毁栈
void StackDestroy(ST* ps)
{assert(ps);free(ps->arr);ps->arr = NULL;ps->top = ps->capacity = 0;
}
//入栈----栈顶
void StackPush(ST* ps, STDataType x)
{if (ps->top == ps->capacity){//增容int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));if (tmp == NULL){perror("realloc");exit(1);}//空间申请成功ps->arr = tmp;ps->capacity = newCapacity;}ps->arr[ps->top++] = x;
}//栈是否为空
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}//出栈----栈顶
void StackPop(ST* ps)
{assert(!StackEmpty(ps));--ps->top;
}//出栈顶数据,元素不会删除
STDataType StackTop(ST* ps)
{assert(!StackEmpty(ps));return ps->arr[ps->top - 1];}//获取栈中有效元素个数
int StackSize(ST* ps)
{return ps->top;
}//非递归版本的快速排序——栈
void QuickSortNoR(int* arr, int left, int right)
{ST st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (!StackEmpty(&st)){//取栈顶两次int end = StackTop(&st);StackPop(&st);int begin = StackTop(&st);StackPop(&st);//[begin,end]找基准值int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[keyi], &arr[prev]);keyi = prev;//begin keyi end//左序列:[begin,keyi-1] 右序列:[keyi+1,end];if (keyi + 1 < end){StackPush(&st, keyi + 1);StackPush(&st, end);}if (begin < keyi - 1){StackPush(&st, begin);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);//QuickSort(a,0,n-1);QuickSortNoR(a, 0, n - 1);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}
优点:
通过栈数据结构模拟了递归调用的过程,避免了递归版本可能出现的栈溢出问题,同时保持了快速排序的时间复杂度特性。
复杂度:
时间复杂度
-
平均情况:O(n log n)
- 每次划分操作将数组分成两部分,大约需要 O (n) 时间
- 整个排序过程需要 log n 层划分(类似二叉树的高度)
- 总时间复杂度为 O (n log n)
-
最坏情况:O(n²)
- 当数组已经有序或接近有序时,每次划分可能将数组分成极不平衡的两部分(例如一个部分只有 1 个元素,另一个部分有 n-1 个元素)
- 此时需要 n 层划分,总时间复杂度退化为 O (n²)
- 可以通过合理选择基准值(如三数取中法)来避免这种情况
空间复杂度
-
平均情况:O(log n)
- 栈中最多存储 log n 个区间信息(对应递归版本的递归调用栈深度)
- 额外空间主要用于栈存储
-
最坏情况:O(n)
- 在极端情况下,栈中可能需要存储 n 个区间信息
- 与递归版本的最坏情况空间复杂度相同
归并排序
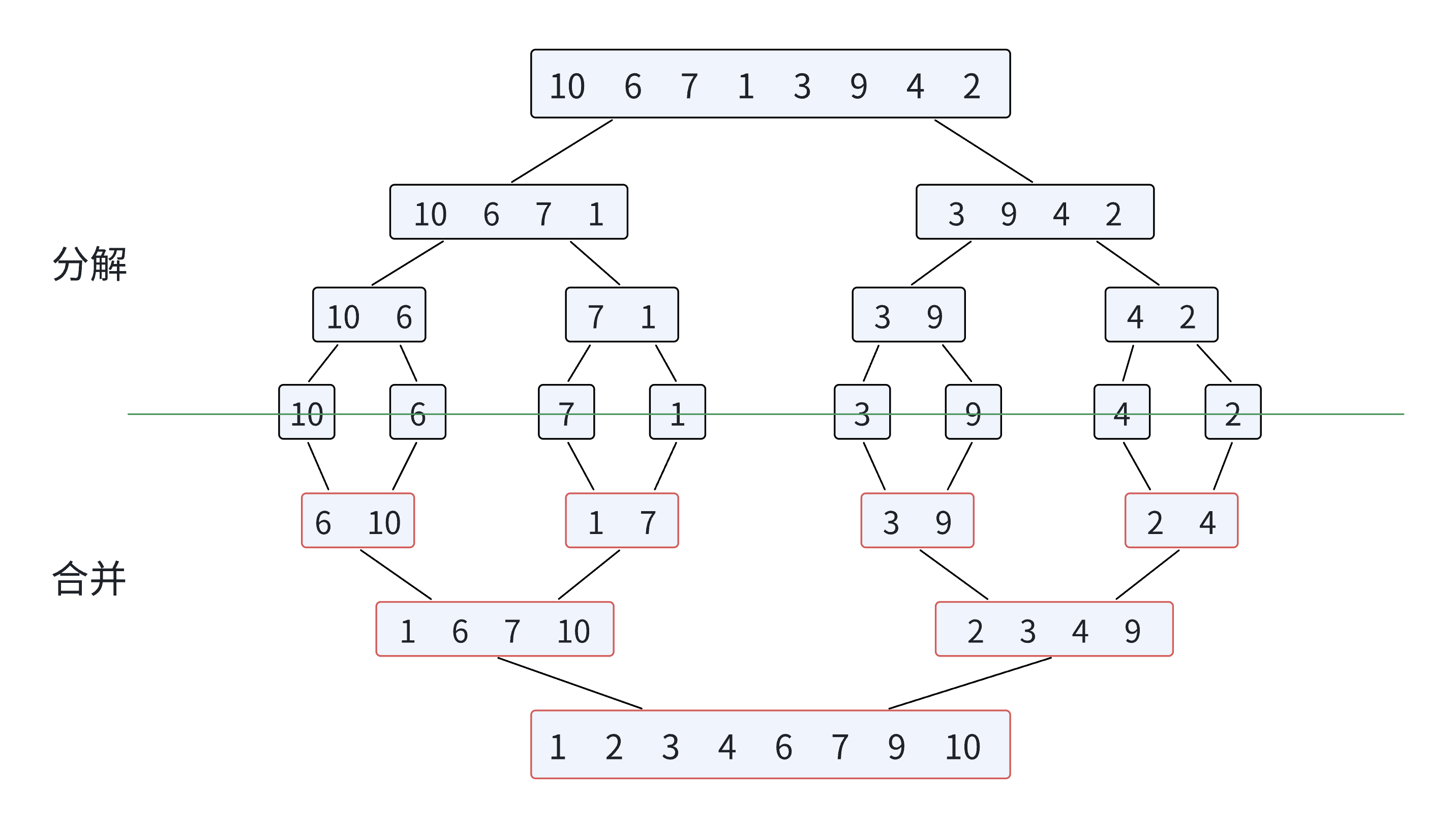
算法思想:
代码实现:
#include<stdio.h>
#include<stdlib.h>//非递归版本的快速排序——栈
void QuickSortNoR(int* arr, int left, int right)
{ST st;StackInit(&st);StackPush(&st, left);StackPush(&st, right);while (!StackEmpty(&st)){//取栈顶两次int end = StackTop(&st);StackPop(&st);int begin = StackTop(&st);StackPop(&st);//[begin,end]找基准值int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[prev], &arr[cur]);}cur++;}Swap(&arr[keyi], &arr[prev]);keyi = prev;//begin keyi end//左序列:[begin,keyi-1] 右序列:[keyi+1,end];if (keyi + 1 < end){StackPush(&st, keyi + 1);StackPush(&st, end);}if (begin < keyi - 1){StackPush(&st, begin);StackPush(&st, keyi - 1);}}StackDestroy(&st);
}//归并排序代码实现
void _MergeSort(int* arr, int left, int right, int* tmp)
{if (left >= right){return;}//left rightint mid = (left + right) / 2;//根据mid划分两个区间[left,mid],[mid+1,right]_MergeSort(arr, left, mid, tmp);_MergeSort(arr, mid + 1, right, tmp);//合并两个有序序列int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = begin1;while (begin1 <= end1 && begin2<=end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else {tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//将tmp中有序数组导入 arr 数组for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}
void MergeSort(int* arr, int n)
{if (arr == NULL || n <= 1)return;int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){printf("malloc fail");exit(1);}_MergeSort(arr, 0, n - 1, tmp);free(tmp);tmp =NULL;
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);//QuickSort(a,0,n-1);//QuickSortNoR(a, 0, n - 1);MergeSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}
复杂度:
时间复杂度
- 最好情况:O(n log n)
- 平均情况:O(n log n)
- 最坏情况:O(n log n)
归并排序的时间复杂度非常稳定,无论输入数据的分布如何(有序、逆序或随机),时间复杂度始终是 O (n log n)。这是因为:
- 归并排序采用分治策略,将数组不断二分,直到子数组长度为 1,这个过程需要 log n 层(类似二叉树的高度)
- 每一层都需要对所有元素进行一次合并操作,总耗时为 O (n)
- 因此总时间复杂度为 O (n log n)
空间复杂度
- 空间复杂度:O(n)
归并排序需要额外的空间来存储合并过程中的临时数组(tmp 数组),其大小与原数组相同,因此空间复杂度为 O (n)。
此外,递归实现的归并排序还需要考虑递归调用栈的空间,递归深度为 log n,所以递归栈的空间复杂度为 O (log n)。但通常在分析归并排序的空间复杂度时,主要考虑的是临时数组的开销,因此整体空间复杂度仍记为 O (n)。
稳定性
归并排序是一种稳定的排序算法,在合并过程中,当两个元素相等时,会优先保留前面的元素,不会改变它们的相对顺序。
计数排序
代码实现:
#include<stdio.h>#include<string.h>
//计数排序
void CountSort(int* arr, int n)
{//找最大和最小值int min = arr[0], max = arr[0];for (int i = 1; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//max-min+1确定count数组的大小int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");exit(1);}//初始化用callocmemset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i] - min]++;}//将count数组还原到原数组中,使其有序int index = 0;for (int i = 0; i < range; i++){while (count[i]--){arr[index++] = i + min;}}
}
void arrprint(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5, 3, 9, 6, 2, 4, 7, 1, 8 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");arrprint(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);//QuickSort(a,0,n-1);//QuickSortNoR(a, 0, n - 1);//MergeSort(a, n);CountSort(a, n);printf("排序之后:");arrprint(a, n);
}int main()
{test01();return 0;
}
时间复杂度
- 最好情况:O(n + range)
- 平均情况:O(n + range)
- 最坏情况:O(n + range)
其中,n是数组元素个数,range是最大值与最小值的差值加 1(即max - min + 1)。
时间复杂度由三部分组成:
- 查找最大值和最小值:O (n)
- 统计元素出现次数:O (n)
- 从计数数组还原到原数组:O (range)
空间复杂度
- 空间复杂度:O(range)
主要开销是计数数组count所占用的空间,大小为range。
特点:
- 非比较排序:不通过元素间的比较来排序,而是利用元素的数值特性
- 稳定性:在还原数组时保持相同元素的相对顺序,是稳定的排序算法
- 适用场景:适合数值范围较小且为整数的数组排序,当
range远小于n时效率很高 - 局限性:不适合浮点数或数值范围极大的整数排序
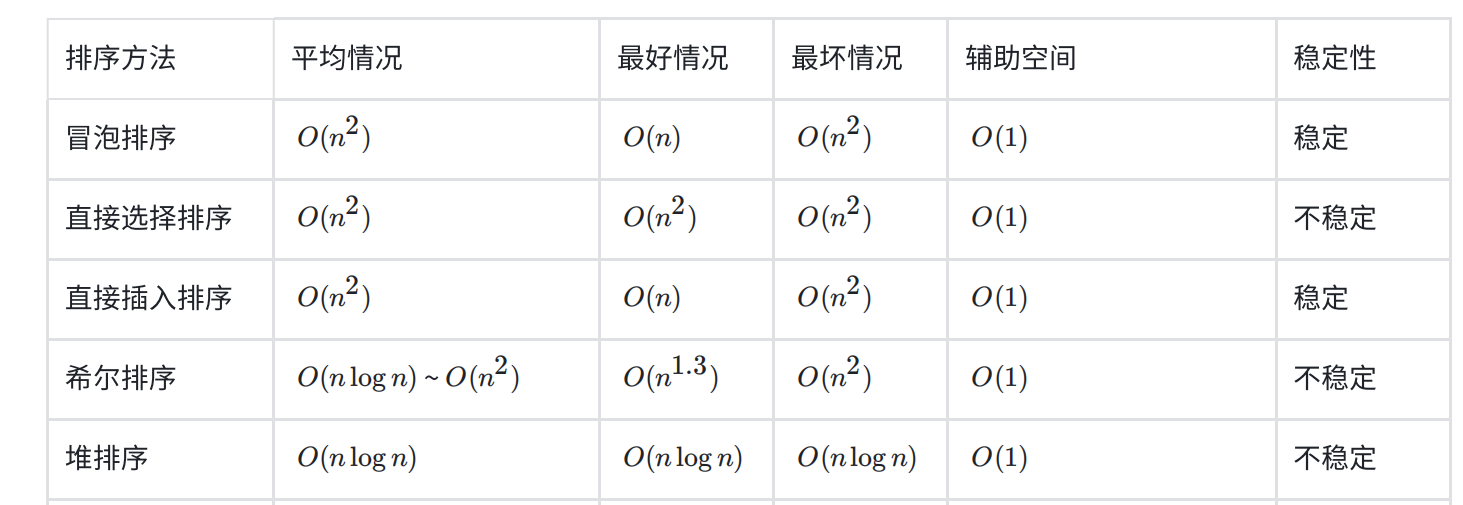
排序比较:
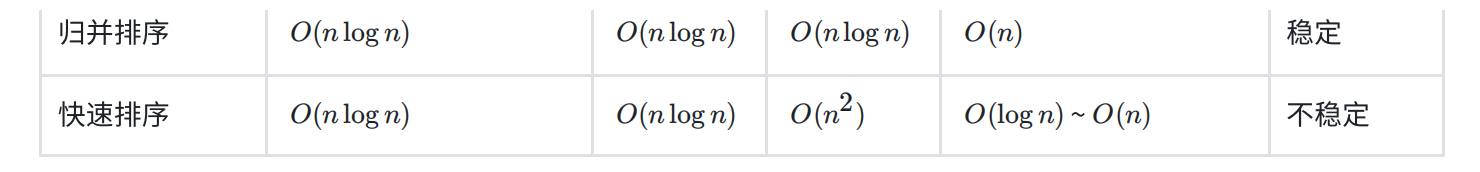
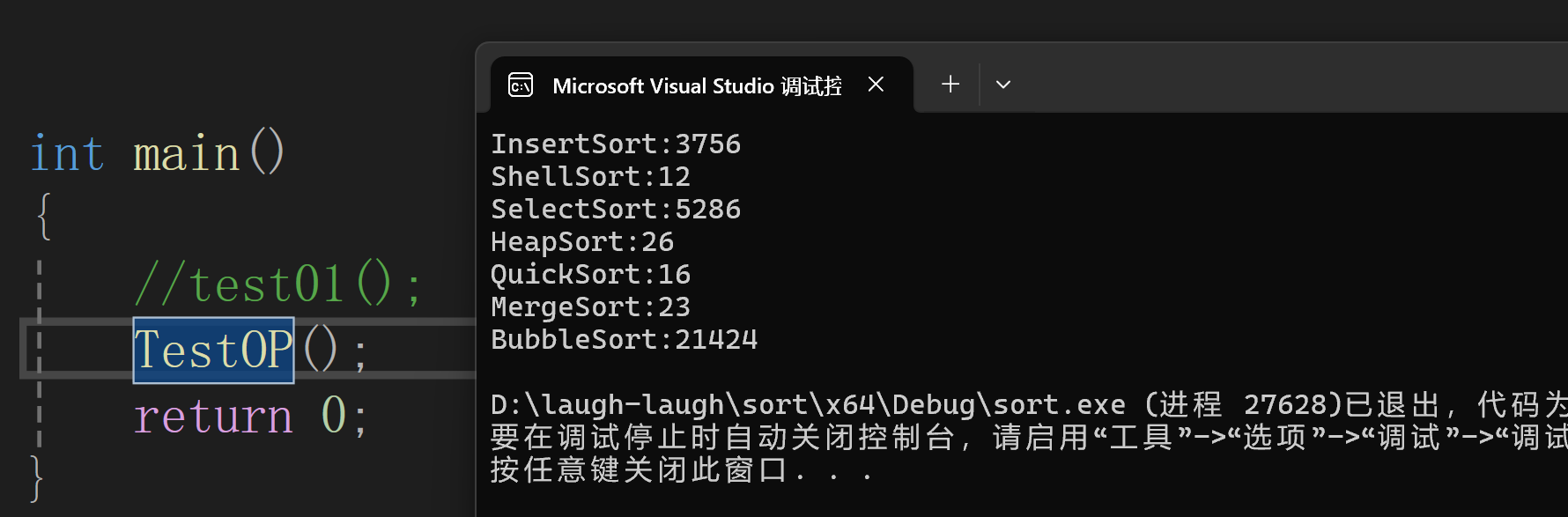
测试代码(不运行):
// 测试排序的性能对⽐
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{//test01();TestOP();return 0;
}