当前位置：首页 > news >正文

机器学习之数据模型训练（三）

news 2025/8/20 8:39:06

多种机器学习模型在分类任务中的对比实验

一、详解网格搜索（Grid Search）调参：原理、实现与应用

1. 什么是网格搜索？

2. 核心思想

3. 与交叉验证的结合

二、多种分类模型对比

1. 逻辑斯蒂回归（Logistic Regression）

1. 参数网格搜索（Grid Search）调优

2. 使用最优参数构建模型

3. 模型预测与评估

2. 随机森林（Random Forest）

3. 支持向量机（SVM）

4. XGBoost

5. 高斯朴素贝叶斯（Gaussian Naive Bayes）

6. AdaBoost

三、结果分析

接上篇我们完成了数据的预处理，将文本转化为了模型可以训练的标准文本。本文我们将进行几种模型的训练，看看哪个模型的效果更明显。

多种机器学习模型在分类任务中的对比实验

在机器学习分类任务中，选择合适的模型往往是提升性能的关键。本文将使用逻辑斯蒂回归、随机森林、支持向量机、XGBoost、高斯朴素贝叶斯和 AdaBoost 六种经典模型，基于同一数据集进行分类实验，并对比各模型的表现。

一、详解网格搜索（Grid Search）调参：原理、实现与应用

1. 什么是网格搜索？

网格搜索是一种穷举式的超参数优化方法。它将每个超参数的可能取值视为一个维度，所有维度的组合构成一个 “参数网格”，然后在这个网格中逐个尝试所有可能的参数组合，通过交叉验证（Cross Validation）评估每个组合的性能，最终选择性能最优的参数组合。

2. 核心思想

把超参数的可能取值用 “网格” 形式列出来（例如：C=[0.1,1,10]，penalty=['l1','l2']）；
遍历网格中的每一个参数组合，训练模型并评估性能；
保留性能最优的参数组合作为最终结果。

3. 与交叉验证的结合

网格搜索通常与交叉验证（如 K 折交叉验证）结合使用，原因是：

二、多种分类模型对比

单一训练集的评估结果可能受数据划分影响，存在随机性；
交叉验证通过多次划分训练集和验证集，取平均性能作为参数组合的评分，结果更稳健。

1. 逻辑斯蒂回归（Logistic Regression）

逻辑斯蒂回归是一种经典的线性分类模型，适用于二分类或多分类任务。

# 以下为参数调优过程（已注释）
# param_grid = [
#     {
#         'solver': ['newton-cg', 'lbfgs', 'sag'],
#         'penalty': ['l2', 'none'],
#         'C': [0.01, 0.1, 1, 10, 100],
#         'max_iter': [100, 200, 300],
#         'multi_class': ['auto', 'ovr', 'multinomial']
#     },
#     {
#         'solver': ['saga'],
#         'penalty': ['l1', 'l2', 'elasticnet', 'none'],
#         'C': [0.01, 0.1, 1, 10, 100],
#         'max_iter': [100, 200, 300],
#         'multi_class': ['auto', 'ovr', 'multinomial'],
#         'l1_ratio': [0.1, 0.5, 0.9]
#     }
# ]
# lr = LogisticRegression()
# grid_search = GridSearchCV(lr, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)# 使用最优参数构建模型
lr = LogisticRegression(C=0.01, max_iter=300, multi_class='auto', penalty='none', solver='lbfgs')
lr.fit(train_data_x, train_data_y)# 预测与评估
pred = lr.predict(test_data_x)
pred1 = lr.predict(train_data_x)
print('逻辑斯蒂回归测试分类报告结果')
print(metrics.classification_report(test_data_y, pred))
print('逻辑斯蒂回归自测分类结果')
print(metrics.classification_report(train_data_y, pred1))

1. 参数网格搜索（Grid Search）调优

# 定义参数网格，包含不同求解器对应的参数组合
param_grid = [{# 第一组：适用于newton-cg、lbfgs、sag求解器的参数'solver': ['newton-cg', 'lbfgs', 'sag'],  # 优化求解器'penalty': ['l2', 'none'],  # 正则化方式（这些求解器不支持l1）'C': [0.01, 0.1, 1, 10, 100],  # 正则化强度的倒数（值越小正则化越强）'max_iter': [100, 200, 300],  # 最大迭代次数'multi_class': ['auto', 'ovr', 'multinomial']  # 多分类策略},{# 第二组：适用于saga求解器的参数（支持更多正则化方式）'solver': ['saga'],'penalty': ['l1', 'l2', 'elasticnet', 'none'],  # saga支持弹性网络等正则化'C': [0.01, 0.1, 1, 10, 100],'max_iter': [100, 200, 300],'multi_class': ['auto', 'ovr', 'multinomial'],'l1_ratio': [0.1, 0.5, 0.9]  # elasticnet专用参数（l1正则化比例）}
]# 初始化逻辑回归模型
lr = LogisticRegression()# 网格搜索：用5折交叉验证（cv=5）遍历所有参数组合
grid_search = GridSearchCV(lr, param_grid, cv=5)
grid_search.fit(train_data_x, train_data_y)  # 在训练数据上拟合# 输出最优参数组合
print('最好的模型参数：')
print(grid_search.best_params_)

核心作用：
通过暴力搜索的方式，从参数网格中找到使模型在交叉验证中性能最优的参数组合，避免人工调参的主观性。

2. 使用最优参数构建模型

# 用最优参数实例化逻辑回归模型（这里展示的是搜索得到的一组最优参数）
lr = LogisticRegression(C=0.01,          # 正则化强度倒数（较小值表示较强正则化）max_iter=300,    # 最大迭代次数（确保模型收敛）multi_class='auto',  # 自动选择多分类策略penalty='none',  # 不使用正则化solver='lbfgs'   # 优化求解器
)# 在训练数据上拟合模型
lr.fit(train_data_x, train_data_y)

核心作用：
基于最优参数配置，在完整训练集上重新训练模型，为后续预测做准备。

3. 模型预测与评估

使用训练好的模型在测试集和训练集上进行预测，并通过分类报告评估性能：

# 在测试集和训练集上进行预测
pred = lr.predict(test_data_x)    # 测试集预测结果
pred1 = lr.predict(train_data_x)  # 训练集预测结果# 输出测试集分类报告（包含精确率、召回率、F1分数等）
print('逻辑斯蒂回归测试分类报告结果')
print(metrics.classification_report(test_data_y, pred))# 输出训练集分类报告（用于判断是否过拟合）
print('逻辑斯蒂回归自测分类结果')
print(metrics.classification_report(train_data_y, pred1))

核心作用：

测试集评估：判断模型的泛化能力（在新数据上的表现）。
训练集评估：与测试集对比，若差距过大，可能存在过拟合或欠拟合问题。

经过训练该模型的报告如下：

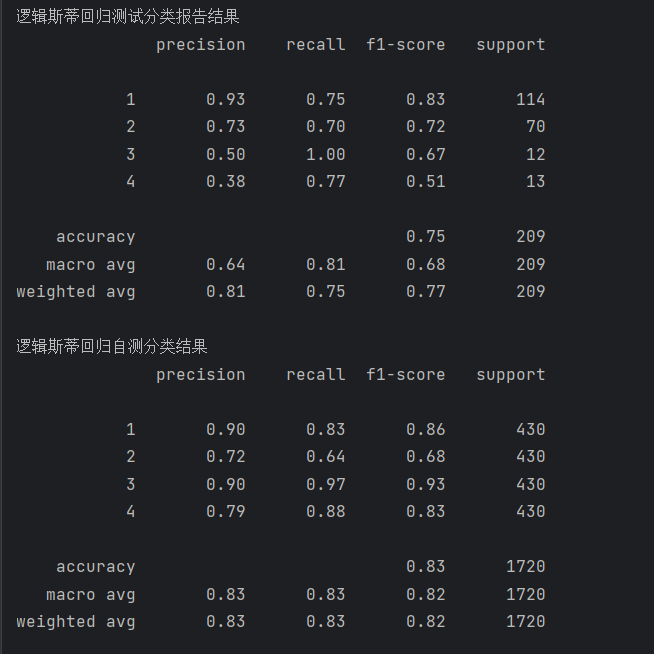
2. 随机森林（Random Forest）

随机森林是一种集成学习模型，由多个决策树组成，具有较强的泛化能力。

# 以下为参数调优过程（已注释）
# param_grid = {
#          'n_estimators': [100,200,300,400,500],
#          'max_depth': [5,10,15,20,25],
#         'min_samples_split':[2,5,10,20,50],
#         'min_samples_leaf':[1,2,5,10]}
# rf = RandomForestClassifier()
# grid_search = GridSearchCV(rf, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)# 使用最优参数构建模型
rf = RandomForestClassifier(max_depth=15, min_samples_leaf=1, min_samples_split=10, n_estimators=300)
rf.fit(train_data_x, train_data_y)# 预测与评估
pred = rf.predict(train_data_x)
pred1 = rf.predict(test_data_x)
print('随机森林自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('随机森林测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

该模型的结果如下：

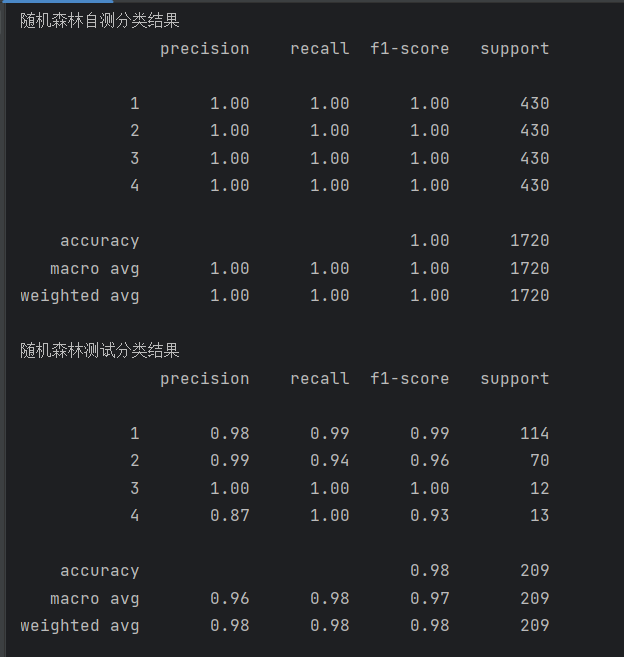
3. 支持向量机（SVM）

支持向量机通过寻找最优超平面来进行分类，在高维空间中表现出色。

# 构建SVM模型
svc = SVC(C=1, kernel='sigmoid', gamma='auto')
svc.fit(train_data_x, train_data_y)# 预测与评估
pred = svc.predict(train_data_x)
pred1 = svc.predict(test_data_x)
print('支持向量机自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('支持向量机测试结果')
print(metrics.classification_report(test_data_y, pred1))

该模型的结果如下：

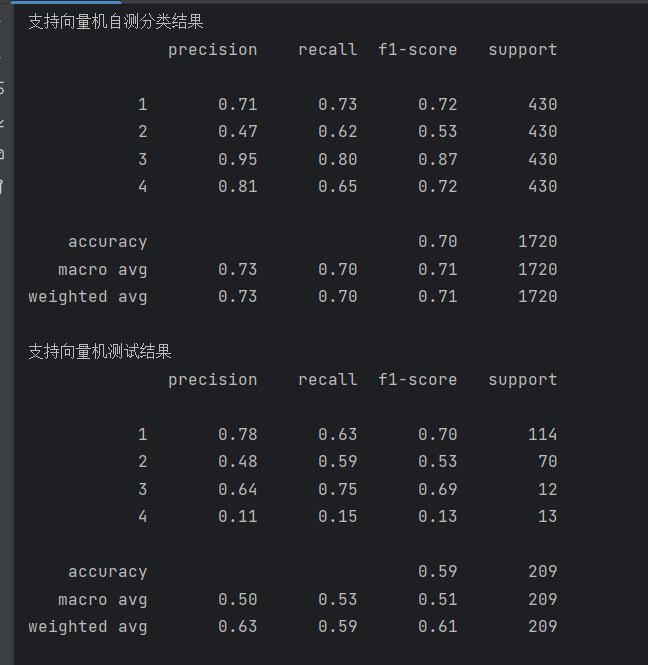
4. XGBoost

XGBoost 是一种高效的梯度提升树模型，在各类竞赛中常取得优异成绩。

# 构建XGBoost模型（需要对标签进行编码）
xgb = XGBClassifier(n_estimators=100, max_depth=3, learning_rate=0.1)
le = LabelEncoder()
train_data_y_encoded = le.fit_transform(train_data_y)
test_data_y_encoded = le.transform(test_data_y)
xgb.fit(train_data_x, train_data_y_encoded)# 预测与评估（需将预测结果解码）
pred_test_encoded = xgb.predict(test_data_x)
pred_train_encoded = xgb.predict(train_data_x)
pred1 = le.inverse_transform(pred_test_encoded)
pred = le.inverse_transform(pred_train_encoded)
print('XGBoost自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('XGBoost测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：

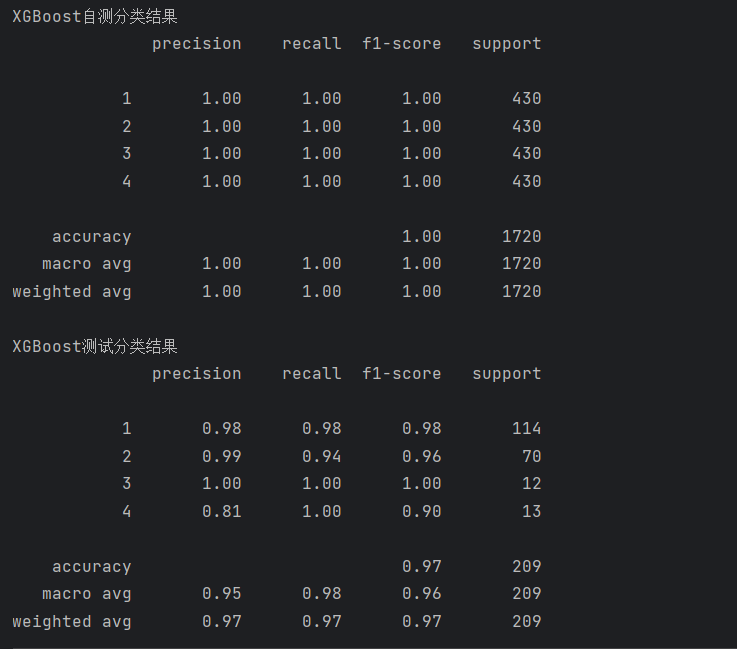
5. 高斯朴素贝叶斯（Gaussian Naive Bayes）

高斯朴素贝叶斯基于贝叶斯定理和特征条件独立假设，计算简单高效。

# 以下为参数调优过程（已注释）
# param_grid = {
#          'var_smoothing': [1e-12,1e-11,1e-10,1e-9],
#          'priors': [[0.2,0.2,0.3,0.3]]}
# gs = GaussianNB()
# grid_search = GridSearchCV(gs, param_grid, cv=5)
# grid_search.fit(train_data_x, train_data_y)
# print('最好的模型参数：')
# print(grid_search.best_params_)# 使用最优参数构建模型
gs = GaussianNB(var_smoothing=1e-12)
gs.fit(train_data_x, train_data_y)# 预测与评估
pred = gs.predict(train_data_x)
pred1 = gs.predict(test_data_x)
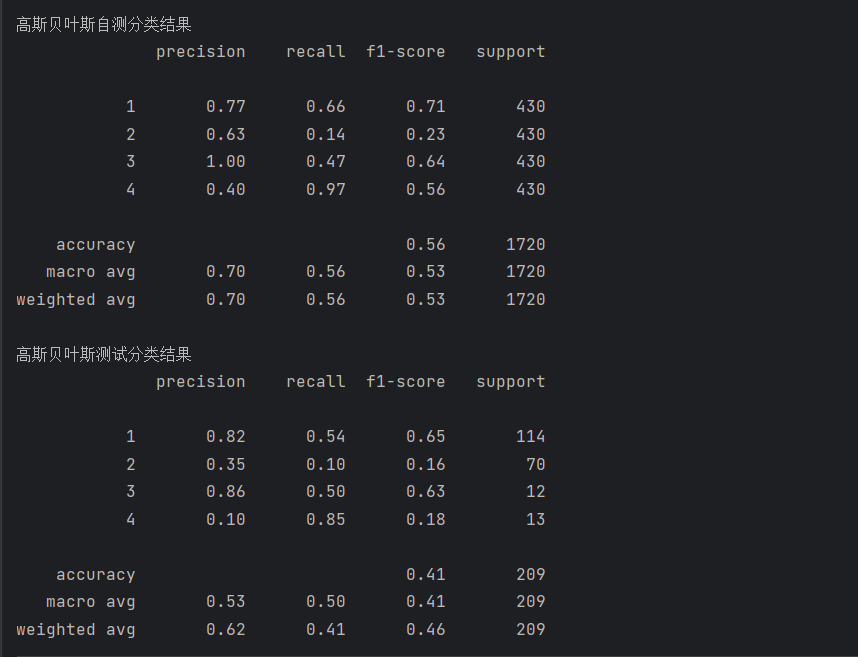
print('高斯贝叶斯自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('高斯贝叶斯测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：

6. AdaBoost

AdaBoost 是一种迭代式的集成学习算法，通过不断调整样本权重来训练弱分类器。

# 构建AdaBoost模型
ada = AdaBoostClassifier()
ada.fit(train_data_x, train_data_y)# 预测与评估
pred = ada.predict(train_data_x)
pred1 = ada.predict(test_data_x)
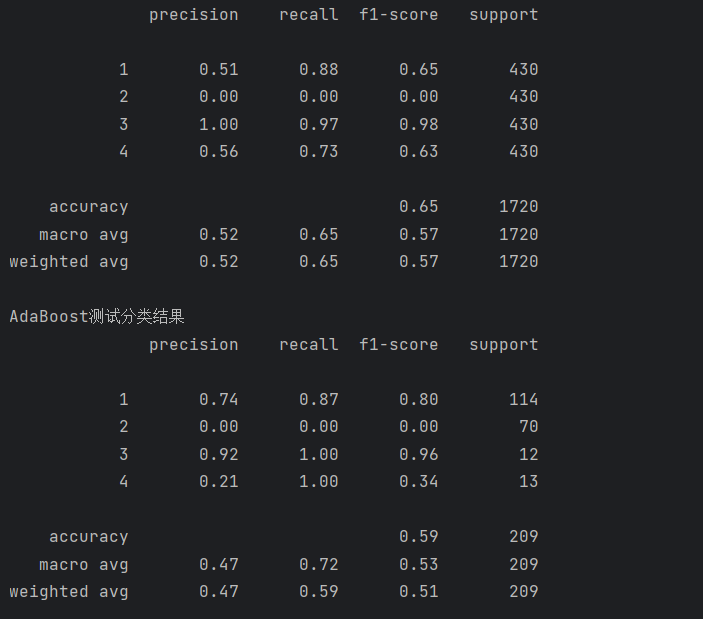
print('AdaBoost自测分类结果')
print(metrics.classification_report(train_data_y, pred))
print('AdaBoost测试分类结果')
print(metrics.classification_report(test_data_y, pred1))

运行结果如下：