当前位置：首页 > news >正文

torch.nn.Conv1d详解

news 2025/8/19 15:03:01

定义：

输出输入：

参数：

注意：

计算复杂度分析：

FLOPs对比dense层：

1. 线性层变换：nn.Linear(10 * E, E)

2. 两层卷积：nn.Conv1d(E, E, kernel_size=3)

参考：

定义：

class torch.nn.Conv1d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

在最简单的情况下，输入大小为 (N, C_in, L)、输出大小为 (N, C_out, L_out) 的该层的输出值可以精确描述为：

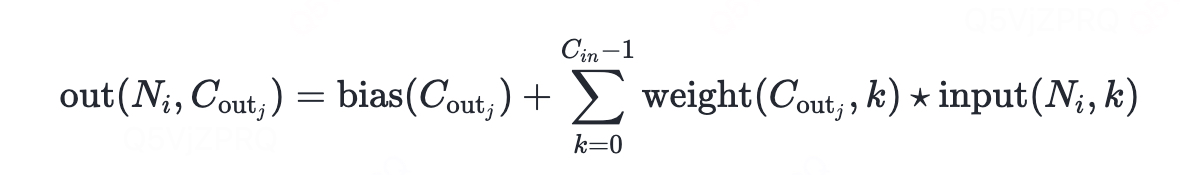
其中：

⋆ 是有效互相关运算符。
N 是批量大小。
C 表示通道数。
L 是信号序列的长度。

输出输入：

(N, C_out, L_out)：

C_out：卷机核个数，也就是输出通道数

L_out：输出长度，计算公式：

参数：

stride: 控制互相关的步长，可以是一个数字或一个单元素元组。
padding: 控制应用于输入的填充量。它可以是字符串 {'valid', 'same'}，也可以是一个整数元组，表示在两侧应用的隐式填充量。
- padding='valid' 等同于无填充。
- padding='same' 会填充输入，使得输出具有与输入相同的形状（长度）。然而，此模式仅支持步长 (stride) 为 1 的情况。
- 当 stride=1、dilation=1 且想让 L_out = length 时，令
  - padding = (kernel_size - 1) // 2 （kernel size应为奇数）
dilation: 控制卷积核点之间的间距；也称为空洞算法 (à trous algorithm)。描述起来较复杂，但此链接很好地展示了 dilation 的作用。
groups: 控制输入和输出之间的连接。in_channels 和 out_channels 都必须能被 groups 整除。例如：
- 当 groups=1 时，所有输入被卷积到所有输出。
- 当 groups=2 时，该操作等效于有两个并排的卷积层，每个层看到一半的输入通道并产生一半的输出通道，然后将两者连接起来。
- 当 groups = in_channels 时，每个输入通道都与自己的一组滤波器（大小为 out_channels / in_channels）进行卷积。（MobileNet 系列）

注意：

1. 输入维度只能是2维或3维，大于3维需要先reshape为3维向量

2. 输入需要将【batch， seq_len， embedding】 reshape为【batch， embedding，seq_len 】，因为一维卷积是在最后维度上扫的

计算复杂度分析：

FLOPs ≈ 2 × L_out × C_in × K × C_out

L_out：输出特征图的长度（相当于二维卷积的H_out/W_out）（可以理解为序列长度？）
C_in：输入通道数
K：卷积核的宽度（一维卷积中只有宽度）
C_out：输出通道数

for c_out in range(C_out): # 每个输出通道
for c_in in range(C_in): # 每个输入通道
for k in range(K): # 卷积核宽度方向
value += input[c_in, i+k] * kernel[c_out, c_in, k]

总FLOPs = (输出位置数量) × (单点计算量)
= L_out × (2 × C_in × K × C_out)
= 2 × L_out × C_in × K × C_out

FLOPs对比dense层：

输入向量：【batch， seq， 10， embedding】

1. 经过nn.Linear(10 * self.embed_dim, self.embed_dim) 做变换

2. 经过2层卷积：nn.Conv1d(in_channels=self.embed_dim, out_channels=self.embed_dim, kernel_size=3)做变化

两者的时间复杂度对比：

1. 线性层变换：`nn.Linear(10 * E, E)`

步骤：

输入形状 [B, S, 10, E] → 先合并最后两维：[B, S, 10*E]
线性层计算：Y = X · W^T + b
- 权重矩阵 W 形状：[E, 10*E]
- 偏置 b 形状：[E]

FLOPs 计算：

矩阵乘法 X · W^T：
每个样本的每个位置（共 B * S 个位置）需要计算：
输入向量 (1×10E) × 权重矩阵 (10E×E) → 输出向量 (1×E)
计算量 = 2 × (10E) × E = 20E²（乘加各算一次）
总乘法 FLOPs = B * S * 20E²
偏置加法（可忽略）：B * S * E（远小于矩阵乘法）

总 FLOPs ≈ 20 B S E²

2. 两层卷积：`nn.Conv1d(E, E, kernel_size=3)`

计算过程：

输入reshape：[B, S, L, E] → [B*S, E, L]
(合并batch和seq维度，通道维在中间)
第一层Conv1d：
- 输入：[B*S, E, L]
- 输出：[B*S, E, L]（假设padding=1保持长度）
- 计算量：2 × L × E × E × 3 = 6L E²
第二层Conv1d：同上，6L E²
总计算量：(6L E² + 6L E²) × (B*S) = 12 B S L E²